Кинематический анализ плоского рычажного механизма 2-го класса

Кинематическим анализом называется изучение движения звеньев без учета сил, обуславливающих это движение.

Кинематический анализ механизмов предусматривает решение трех основных задач:

1) определение положения звеньев и траекторий отдельных точек механизма;

2) определение скоростей точек и угловых скоростей звеньев механизма;

3) определение ускорений точек и угловых ускорений звеньев механизма.

Решение этих задач может быть выполнено графическим или аналитическим методами. Графический метод имеет меньшую точность по сравнению с аналитическим, но является более наглядным.

При графическом методе кинематического анализа первая задача решается методом планов положений, вторая – методом планов скоростей и третья – методом планов ускорений механизма. Рассмотрим применение этих методов на конкретных примерах.

2.1. Метод плана положений

Для решения задачи необходимо построить последовательные положения механизма (планы положений механизма), число которых определяется требуемой точностью результатов кинематического анализа. В рассматриваемом курсе строится одно положение механизма, в зависимости от исходных данных в задании. Кинематическую схему механизма вычерчивают в масштабе, используя масштабный коэффициент длины звеньев .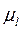

Под масштабным коэффициентом понимают число, показывающее сколько единиц некоторой величины изображает 1 мм чертежа.

Действительные длины звеньев (см. рис. 1.3) условимся обозначать буквой 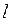с индексом названия звена, например 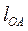, 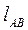. Длины этих же звеньев, изображенных на кинематической схеме в масштабе, будем обозначать 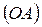, 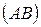.Таким образом, масштабный коэффициент длины звеньев 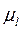определяется формулой:

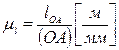. (2.1)

При построении кинематической схемы механизма в масштабе длину отрезка 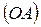выбирают самостоятельно, в соответствии с форматом чертежа. После определения масштабного коэффициента длины звеньев 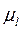, величины остальных отрезков определяют формулой:

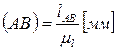. (2.2)

За начальное положение механизма выбирается положение, когда угол поворота кривошипа 1 равен нулю (рис. 2.1).

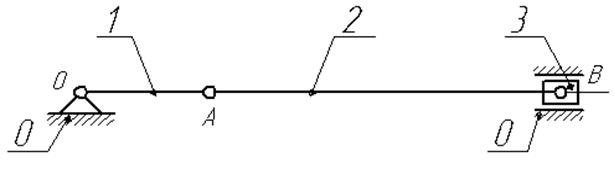
Рис. 2.1.Кинематическая схема механизма в начальном положении

Пример №2.Построить по исходным данным план положения механизма, представленного на рис. 1.3.

Дано: 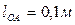, , 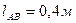, 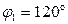направление вращения кривошипа – против хода часовой стрелки.

Решение:

Принимаем при построении длину кривошипа 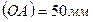. Тогда масштабный коэффициент длины по формуле (2.1) будет равен:

.

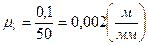Длину отрезка 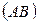определим по формуле (2.2): .

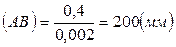Строим кинематическую схему механизма (рис. 2.2)

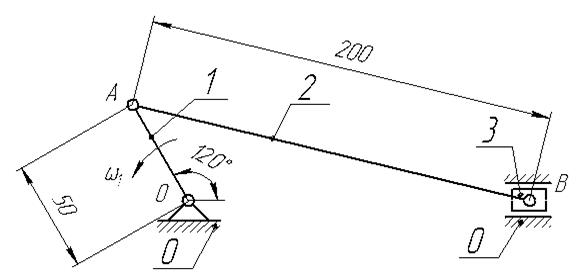
Рис. 2.2. Кинематическая схема механизма в заданном положении

2.2. Метод планов скоростей

Сущность графического метода построения планов скоростей и ускорений основана на использовании векторных уравнений, связывающих скорости, а также ускорения отдельных точек звеньев механизма с последующим их решением графическим путем.

Составим векторные уравнения, связывающие скорости точек звеньев механизма (рис. 2.2). Звено 1 совершает вращательное движение вокруг неподвижной стойки 0. Скорость точки А определяется формулой:

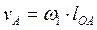. (2.3)

Вектор 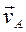перпендикулярен (ОА) и направлен в сторону вращения кривошипа, т.е. по .

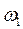Точка В совершает плоскопараллельное движение. По теореме о сложении скоростей скорость точки Bнаходится как сумма скорости полюса и скорости точки В во вращательном движении вокруг полюса:

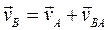, (2.4)

где 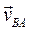– вектор относительной скорости точки B во вращательном движении вокруг полюса A;

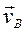– вектор скорости точки В относительно стойки О.

Вектор скорости 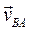перпендикулярен шатуну 2 и определяется по формуле:

,

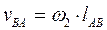где 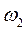– угловая скорость шатуна 2 (она пока неизвестна).

Поскольку ползун В относительно стойки движется поступательно, то вектор скорости 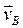лежит на прямой, параллельной движению ползуна (в нашем случае параллельно (ОВ)). Строим в общем виде план скоростей для положения механизма, представленного на рис.2.2 (см. рис. 2.3).

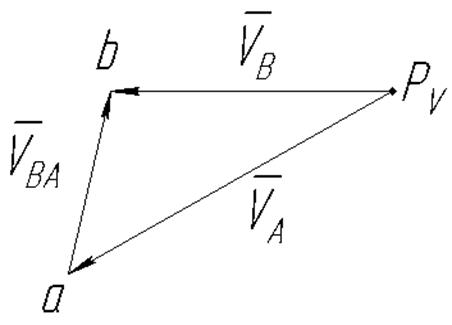
Рис. 2.3. План скоростей механизма

При построении планов скоростей используют масштабный коэффициент скорости 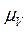, который определяется формулой:

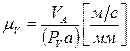, (2.5)

где 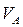– значение скорости точки А, полученное по формуле (2.3);

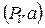– расстояние на плане скоростей от полюса 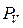до точки а (выбирается самостоятельно в соответствии с форматом чертежа, мм).

Для определения численного значения скорости точки В, воспользуемся формулой:

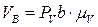, (2.6)

где 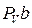– расстояние на плане скоростей от полюса 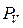до точки b (мм).

Угловую скорость движения шатуна 2определяем по формуле:

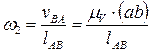, (2.7)

где 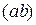– величина отрезка, взятого из плана скоростей (мм).

На планах скоростей и ускорений принято скорости и ускорения точек обозначать маленькими латинскими буквами.

При проведении кинематического анализа рычажных механизмов необходимо построить планы скоростей для всех последовательных положений механизма.

2.3. Теорема подобия для плана скоростей

Теорема. Отрезки прямых линий, соединяющие концы векторов абсолютных скоростей точек на плане скоростей, и отрезки прямых линий, соединяющие одноименные точки на плане механизма, образуют подобные и сходственно расположенные фигуры. Фигура на плане скоростей повернута на 90° относительно фигуры на плане механизма.

Доказательство. Построим в общем виде план скоростей для механизма, изображенного на рис. 2.4а.

1. Найдем скорость точки А: 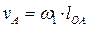. Вектор 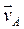перпендикулярен кривошипу ОА и направлен в сторону его вращения.

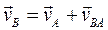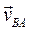2. Определим скорость точки В. Шатун 2 совершает плоскопараллельное движение. На основании теоремы о скоростях точек тела, совершающих такое движение, составим векторное равенство: , где – скорость точки В относительно точки A во вращательном движении шатуна 2 вокруг А; следовательно, вектор 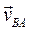перпендикулярен отрезку АВ. Одновременно точка В принадлежит ползуну 3, совершающему возвратно-поступательное движение вдоль оси Ох; следовательно, вектор 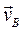параллелен оси Ох.

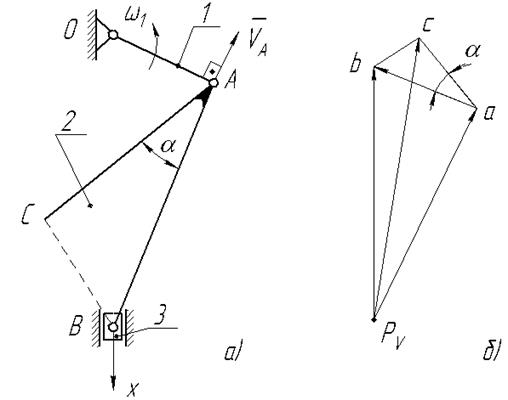
Рис. 2.4

3. Построим план скоростей (рис. 2.4б):

– из произвольной точки 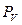проведем луч, перпендикулярный ОА, в направлении вращения кривошипа 1 и отложим на нем отрезок 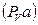произвольной длины;

– через точку а проведем прямую, перпендикулярную АВ, а через полюс 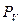– прямую, параллельную оси Ох;

– на пересечении этих прямых получим точку b. Вектор 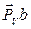– скорость точки В в масштабе .

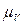4. Определим скорость точки С шатуна 2. На основании теоремы о скоростях точек тела, совершающего плоскопараллельное движение, составим два векторных равенства:

; ,

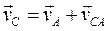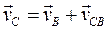где 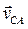–скорость точки С, относительно точки А во вращательном движении шатуна 2 вокруг А; следовательно, вектор 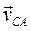перпендикулярен отрезку АС;

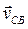– скорость точки С, относительно точки В во вращательном движении шатуна 2 вокруг В; следовательно, вектор 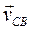перпендикулярен отрезку ВС.

5. На плане скоростей через точку а проведем прямую, перпендикулярную АС, а через точку b – прямую, перпендикулярную ВС. Их пересечение дает точку с.

В результате построений мы получили на плане скоростей треугольник abc, подобный треугольнику АВС плана механизма. Признак подобия – взаимная перпендикулярность сторон. Таким образом, п.4 и 5 являются непосредственным доказательством теоремы подобия для плана скоростей.

Соединим точку с с полюсом плана скоростей. Вектор 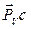– скорость точки С в масштабе .

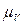Пример №3. Построить по исходным данным план скоростей механизма, представленного на рис. 2.5а и определить скорости всех указанных точек, а также угловые скорости звеньев.

Дано: , , , , , .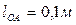

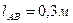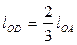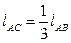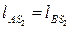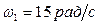Построить план скоростей механизма и определить: , , , , , .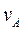

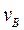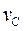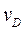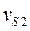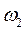Решение:

Скорость точки А определяем по формуле (2.3):

.

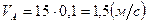На плане скоростей строим отрезок 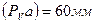. Тогда масштабный коэффициент скорости по формуле (2.5) будет равен: .

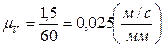По теореме о сложении скоростей скорость точки B равна 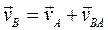. Из точки а на плане скоростей проводим луч, перпендикулярный АВ, соответствующий вектору скорости 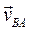, а из полюса 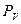проводим луч, параллельный ОВ, т.е. параллельный ходу движения ползуна, соответствующий вектору скорости 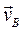. Точка пересечения лучей b соответствует концу вектора скорости точки В. Строим план скоростей (рис 2.5б).

Для того чтобы определить численное значение точки В, воспользуемся формулой (2.6):

.

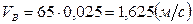Найдем скорости остальных точек. Поскольку все точки звеньев совершают плоскопараллельное движение, то воспользуемся теоремой подобия для плана скоростей. Рассмотрим точку S₂. Она принадлежит звену 2 и делит шатун АВ посередине. На плане скоростей точка s₂ также будет делить отрезок аb пополам. Расстояние от полюса 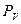до s₂ и будет определять скорость точки S₂.

Точка С тоже принадлежит звену 2 и расположена на расстоянии 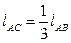. На плане скоростей она так же будет отстоять от точка а на расстоянии 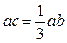. Соединяем полюс и точку с – этот и есть вектор скорости точки С.

Рассмотрим точку D. Она принадлежит звену 1. Порядок определения скорости точки Dаналогичен точке С. План скоростей построен.

После определения направлений скоростей точек на плане скоростей, определим численное значение скоростей точек аналогично определению численного значения скорости точки В:

,

,

.

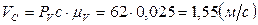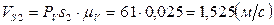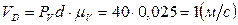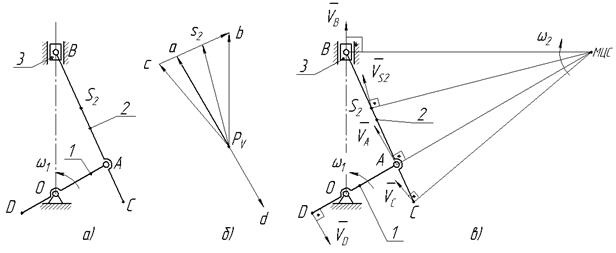
Рис. 2.5

Угловую скорость движения шатуна 2определяем по формуле (2.7):

.

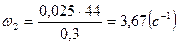Проверим правильность построения плана скоростей (рис. 2.5в). Для того чтобы узнать направления скоростей точек звена 2, построим мгновенный центр скоростей (МЦС): направление и значение скорости точки А нам известно, а также известна траектория движения ползуна В. По направлению вектора скорости точки А определяем направление угловой скорости шатуна 2 – 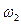. Соединив МЦС с точками S₂ и С, находим направления векторов скоростей этих точек, согласно направлению 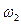. Направление скорости точки D перпендикулярно кривошипу 1 и направлено в сторону его вращения.

Из построений видно, что направления векторов скоростей обоих методов совпадают.

2.4. Метод планов ускорений

Для построения плана ускорений для заданного на рис. 2.2 положения механизма составим векторные уравнения, связывающие ускорения точек звеньев механизма.

Ускорение точки А принадлежащей кривошипу 1, вращающегося с постоянной угловой скоростью 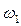определяется формулой:

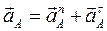, (2.8)

где 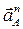– вектор нормального ускорения точки А;

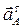– вектор касательного ускорения точки А.

Нормальное ускорение всегда направлено от точки к центру вращения (в нашем случает от точки А к центру О) и определяется формулой:

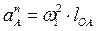. (2.9)

Касательное ускорение всегда направлено по касательной к траектории движения точки и выражается формулой:

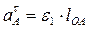, (2.10)

где 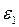– угловое ускорение кривошипа 1.

По условию задачи кривошип вращается равномерно, т.е. 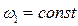, следовательно, здесь (и в последующих примерах) его угловое ускорение равно нулю: .

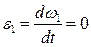Подставляя (2.9) и (2.10) в уравнение (2.8) получаем:

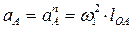. (2.11)

При построении планов ускорений используют масштабный коэффициент ускорения 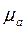, который определяется формулой:

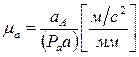, (2.12)

где 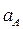– значение ускорения точки А, полученное по формуле (2.11);

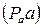– расстояние на плане ускорений от полюса 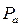до точки а (выбирается самостоятельно в соответствии с форматом чертежа, мм).

Поскольку точка В движется плоскопараллельно, то ускорение точки В равно сумме ускорения полюса и ускорения данной точки во вращательном движении вокруг полюса:

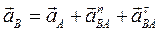, (2.13)

где 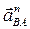– вектор нормального ускорения точки В относительно полюса А; 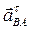– вектор касательного ускорения точки В относительно полюса А;

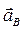– вектор ускорения точки В относительно стойки О.

Нормальное ускорение 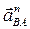направлено вдоль АВ от точки В к центру вращения – полюсу А и определяется формулой:

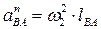. (2.14)

Величина отрезка на плане ускорений, соответствующего значению 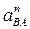, определяется формулой:

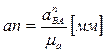. (2.15)

Касательное ускорение всегда направлено по касательной к траектории движения точки (перпендикулярно АВ) и выражается формулой:

,

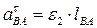где 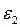– угловое ускорение шатуна 2 (оно пока не известно).

Поскольку ползун В движется поступательно, то вектор ускорения 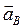лежит на прямой, параллельной движению ползуна (в нашем случае параллельно (ОВ)).Строим в общем виде план ускорений для положения механизма, представленного на рис.2.2 (см. рис. 2.6).

Порядок построения плана ускорений следующий: от полюса 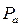строим ускорение точки А. Затем из конца вектора 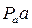проводим отрезок 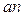, соответствующий вектору нормального ускорения 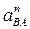. Через точку п проводим луч, перпендикулярный 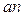. С другой стороны, из полюса 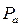проводим луч, параллельный ходу движения ползуна В, соответствующий вектору ускорения 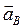. Точка пересечения лучей даст нам ускорение точки В – b.

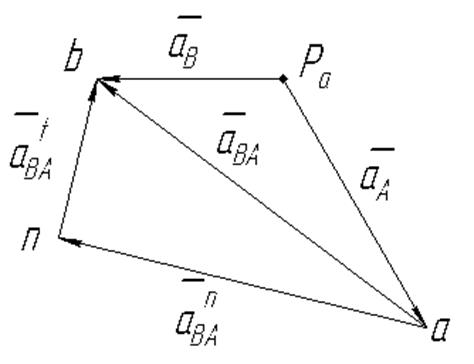
Рис. 2.6. План ускорений механизма

Для определения численного значения ускорения точки В, воспользуемся формулой:

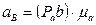, (2.16)

где 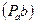– расстояние на плане ускорений от полюса 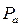до точки b (мм).

Угловое ускорение движения шатуна 2определяем по формуле:

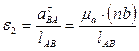, (2.17)

где 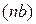– величина отрезка, взятого из плана скоростей (мм).

2.5. Теорема подобия для плана ускорений

Теорема. Отрезки прямых линий, соединяющие концы векторов абсолютных ускорений точек на плане ускорений, и отрезки прямых линий, соединяющие одноименные точки на плане механизма, образуют подобные и сходственно расположенные фигуры.

Рассмотрим применение теоремы подобия для плана ускорений на примере механизма, изображенного на рис. 2.7а.

Построим в общем виде план ускорений для этого механизма.

1. Определим ускорение точки А кривошипа. В общем случа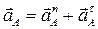е , где 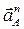– нормальное ускорение; 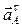– тангенциальное ускорение. Численно 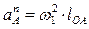; 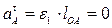, поскольку по условию задачи кривошип вращается равномерно. Таким образом, полное ускорение точки А равно ее нормальному ускорению: .

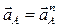Вектор 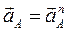направлен вдоль звена ОА от точки А к точке О (см. рис. 2.7а).

Рис. 2.7

2. Определим ускорение точки В шатуна 2. На основании теоремы об ускорениях точек тела, совершающего плоскопараллельное движение, составим векторное равенство: 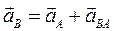, где 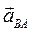– ускорение точки В относительно точки А во вращательном движении шатуна 2 вокруг А; так как это движение неравномерное, то 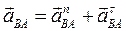, следовательно, 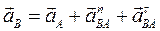, где 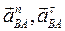– соответственно нормальное и тангенциальное ускорения точки В в этом движении.

Вектор 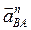направлен вдоль отрезка АВ от точки В к точке А (см. рис. 2.7а); вектор 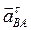перпендикулярен отрезку ВА; точка В одновременно принадлежит звену 3, совершающему возвратно-поступательное движение вдоль оси Ох; следовательно, вектор 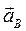параллелен оси Ох. Численно .

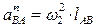3. Зададимся длиной отрезка 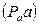и вычислим длину вектора, изображающего на плане ускорений : .

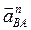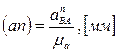4. На основании равенства 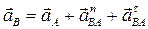выполним построения (рис. 2.7б):

– из точки 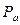проведем луч, параллельный кривошипу ОА, в направлении вектора 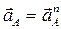(см. рис. 2.7а) и отложим на нем отрезок ;

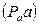– из точки а проведем луч, параллельный отрезку АВ шатуна 2, в направлении вектора 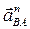(см. рис. 2.7а) и отложим на нем отрезок а п;

– через точку п проведем прямую, перпендикулярную АВ, а через точку 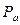– прямую, параллельную оси Ох; их пересечение дает точку b. Вектор 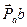– ускорение точки В в масштабе ;

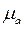– соединим на плане ускорений точку b с точкой а.

5. Определим ускорение точки С. Применим теорему подобия для плана ускорений:

– для построения на плане ускорений 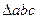, подобного 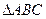, на плане механизма составим две пропорци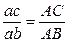и

и ,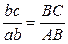

откуда получим

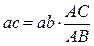и 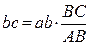, (2.18)

где 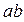– длина отрезка на плане ускорений, мм;

АВ, АС, ВС – длины отрезков на плане механизма, мм, которые могут быть получены измерением на плане механизма или взяты из условия задачи;

– используя результаты вычислений по формулам (2.18), выполним построения. Применим метод засечек: из точки а плана ускорений проведем дугу окружности раствором циркуля, равным ас. Из точки b проведем дугу окружности раствором циркуля, равным bc. Пересечение этих дуг дает точку с. При этом возможно два положения точки с, но верным является только одно из них. Правильность построений определяется условием сходственного расположения треугольников на плане ускорений и на плане положений механизма: если обходить вершины сторон треугольника АВС по ходу часовой стрелки, то получим последовательность их расположения А, В, С. Значит и при обходе вершин треугольника abc на плане ускорений по ходу часовой стрелки мы должны получить ту же последовательность их расположения – а, b, с. Это условие выполняется только при расположении точки с правее отрезка аb (см. рис. 2.7б).

Соединим точку с с полюсом 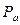. Вектор 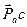– ускорение точки С в масштабе .

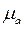Пример №4.Для заданного механизма (рис. 2.5а) построить план ускорений и определить ускорения всех точек, а также угловые ускорения всех звеньев механизма. Исходные данные взять из примера №3.

Дано: , , , , , , .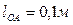

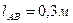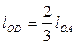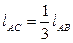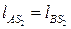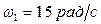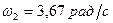Построить план ускорений механизма и определить: , , , , , .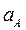

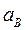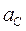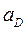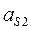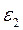Решение:

Ускорение точки А определяем по формуле (2.11):

.

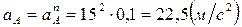На плане ускорений отмечаем полюс 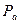и строим отрезок 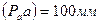в направлении вектора 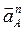(рис. 2.8а). Тогда масштабный коэффициент ускорения по формуле (2.12) будет равен:

.

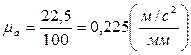По теореме о сложении ускорений при плоскопараллельном движении ускорение точки B равно 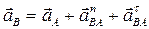. Нормальную составляющую ускорения 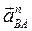определим по формуле (2.14):

.

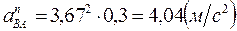Отрезок на плане ускорений, соответствующий данному вектору нормального ускорения по формуле (2.15) будет равен:

.

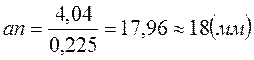Из точки а на плане ускорений проводим луч, параллельный АВ, в направлении вектора 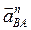(рис. 2.8а) и отложим на нем отрезок 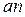. Через точку п проведем прямую, перпендикулярную АВ (это линия действия вектора 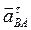), а из полюса 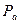прямую, параллельную ОВ – соответствующую направлению вектора 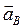. Их пересечение дает точку b(рис. 2.8б).

Для определения численного значения ускорения точки В, воспользуемся формулой (2.16):

.

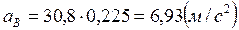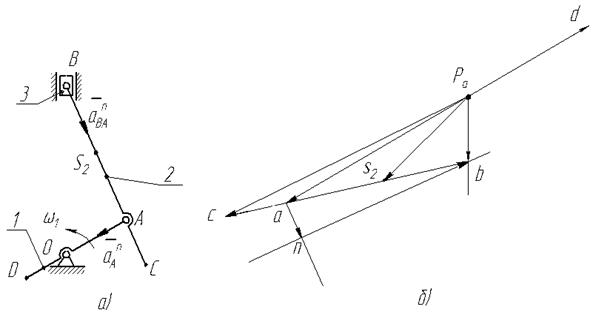
Рис. 2.8

Угловое ускорение движения шатуна 2определяем по формуле (2.17):

.

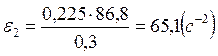Найдем ускорение остальных точек. Поскольку все точки звеньев совершают плоскопараллельное движение, то воспользуемся теоремой подобия для плана ускорений. Рассмотрим точку S₂. Она принадлежит звену 2 и делит шатун АВ посередине. На плане ускорений точка s₂ также будет делить отрезок аb пополам. Расстояние от полюса 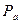до s₂ и будет определять ускорение точки S₂.

Точка С тоже принадлежит звену 2 и расположена на расстоянии 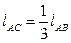. На плане ускорений она так же будет отстоять от точка а на расстоянии 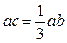. Соединяем полюс и точку с – этот и есть вектор скорости точки С.

Рассмотрим точку D. Она принадлежит звену 1.

Порядок определения ускорения точки D аналогичен точке С.

План ускорений построен.

После определения направлений ускорений точек на плане ускорений, определим численное значение ускорений точек аналогично определению численного значения ускорения точки В:

,

,

.
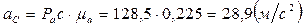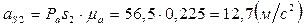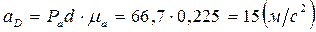3. КИНЕТОСТАТИКА ПЛОСКОГО РЫЧАЖНОГО МЕХАНИЗМА

ГО КЛАССА

Основной задачей кинетостатического (силового) анализа механизмов является определение реакций в кинематических парах. Значение этих сил необходимо при расчете звеньев механизма на прочность, жесткость, виброустойчивость, износостойкость, при расчете подшипников на долговечность и проведении других подобных расчетов, выполняемых при проектировании механизмов.

Если свободному перемещению данного тела в пространстве не препятствуют другие тела, оно называется свободным. Если другие тела путем непосредственного контакта с данным телом мешают ему свободно перемещаться в пространстве, оно называется несвободным, а эти другие тела называются связями по отношению к данному телу.

Силы, с которыми связи действуют на данное тело, называются реакциями связей (пассивными силами). Если сила не является реакцией связи, то она является активной или задаваемой. Иначе – активными называются силы, появление которых не связано с непосредственным контактом или соприкосновением тел (например, силы гравитационного, электромагнитного взаимодействия, другие силы, физическая природа возникновения которых может быть неизвестна, но они не являются реакциями связей).

Принцип освобождаемости от связей. Любое несвободное тело можно условно считать свободным, если действие наложенных на него связей заменить реакциями этих связей.

Все силы, действующие на данное тело (систему тел), могут быть разделены на внешние и внутренние. Внешние – это силы 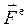, действующие на данное тело или его точки со стороны других тел. Внутренние – это силы 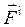взаимодействия между точками или частями данного тела (системы тел). Все внутренние силы абсолютно твердого тела образуют уравновешенную систему сил. Реакции внешних связей для данного тела всегда являются внешними силами.

Деление сил на внешние и внутренние является условным. Все зависит от того, что выбрано за объект исследования, что принято за данную или рассматриваемую механическую систему. Например, объект исследования – двигатель внутреннего сгорания. Давление поршня на кривошип и давление кривошипа на поршень – внутренние силы. Те же силы будут внешними, если объект исследования – отдельно рассматриваемый поршень или кривошип.

Дополнительная задача динамического анализа механизмов состоит в определении уравновешивающей силы или уравновешивающего момента, приложенных к кривошипу. Эти силовые факторы являются функциями положения кривошипа и в данный момент обеспечивают его состояние покоя или равномерного вращательного движения

Кинетостатический расчет механизмов ведется по структурным группам, так как они обладают нулевой подвижностью и, следовательно, являются статически определимыми системами. Кинетостатический расчет начинается с расчета структурной группы, в которую входит самое удаленное ведомое звено механизма, и завершается расчетом ведущего звена – кривошипа.

При выполнении кинетостатического расчета механизма должен быть задан закон движения ведущего звена и проведен полный кинематический анализ. Кроме того, должны быть заданы все внешние силы, действующие на механизм, например, силы «полезного» (производственного) сопротивления. К данным силам также относятся силы тяжести звеньев, которые определяются формулой:

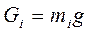, (3.1)

где 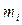– масса i-го звена, (кг);

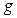– ускорение свободного падения, 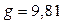(м/с²).

Кинетостатический расчет механизмов основан на использовании принципа Даламбера.