Перевод чисел в десятичную систему счисления. Двоично-десятичная система счисления

Для перевода числа из двоичной или шестнадцатеричной систем счисления в десятичную необходимо данное число представить в развернутом виде, т.е. в виде суммы степеней основания (2;16), умноженных на коэффициенты, соответствующие цифрам переводимого числа, а затем рассчитать сумму.

Например,

6 5 4 3 2 1 0

1001101₂ = 1 * 2⁶ + 0 * 2⁵ + 0 * 2⁴ + 1 *2³ + 1 * 2² + 0 * 2¹ + 1 *2⁰ = 64 + 0 + 0 + 8 + 4 + 0 + 1 = 76₁₀

4 3 2 1 0 -1 -2 -3

11011,011₂ = 1 * 2⁴ + 1 * 2³ + 0 * 2² + 1 * 2¹ + 1 *2⁰ + 0 * 2^-1 + 1 * 2^-2 + 1 * 2^-3 =

= 16 +8 + 0 + 2 + 1 + 0 + 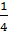+ 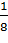= 27 = 27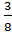,375₁₀

2 1 0

14B = 1 * 16² + 4 * 16¹ + 11* 16⁰ = 256 + 64 + 11 = 331₁₆

3 2 1 0 -1 -2

2A0C,48₁₆ = 2 * 16³ + 10 * 16² + 0 * 16¹ + 12 * 16⁰ + 4 *16^-1 + 8 * 16^-2 = 8192 +2560 + 0 + 12 + 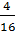+ 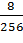= 10764 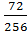= 10764,28125₁₀

При переводе числа из шестнадцатеричной системы счисления в двоичную каждая цифра заменяется тетрадой. Например,

6В71,0С₁₆ = 0110 1011 0111 001, 0000 1100₂

D4В, 5А₁₆ = 1101 0100 1011, 0101 1010₂

Для перевода смешанных чисел из двоичной системы счисления в шестнадцатеричное двоичное число разбивают на тетрады влево и вправо от запятой, крайние тетрады дополняют нулями, а затем заменяют каждую из них соответствующей шестнадцатеричной цифрой системы счисления:

101100001,001₂ = 161,2₁₆

11000101001,1011₂ = 629,В₁₆

При переводе десятичных чисел в двоичные используется двоично-десятичная запись чисел, сущность которой заключается в том, что каждая десятичная цифра представляется четырехразрядным двоичным числом (тетрадой).

Например,

197,36₁₀ = 0001 1001 0111,00110110_2-10

705,425₁₀ = 0111 0000 0101,0100 0010 0101_2-10

Перевод чисел из десятичной системы счисления в двоичную можно выполнить проще и быстрее, используя шестнадцатеричную систему счисления в качестве промежуточной.

Например,

396, 29₁₀ = 18С,4А3₁₆ = 0001 1000 1100,0100 1010 0011₂

396 / 16 = 24, (остаток 12), 12 > 16 24 / 16 = 1, (остаток 8), 8 < 16   39610 = 18С16

0,29 * 16 = 4,64 0,64 * 16 = 10,24 0,24 * 16 = 3,88 0,2910 = 0,4A316

396, 29₁₀ = 18С,4А3₁₆

Задания для самостоятельно выполнения

Задание 6.

6.1. Перевести целые десятичные числа в двоичную систему счисления.

2410 1810 13410 17710 778110

385010 4000810 24510 3310 29810

6.2. Перевести целые десятичные числа в шестнадцатеричную систему счисления.

4310 5810 9910 18410 34710

59310 694410 387510 164810 423110

Задание 7.

7.1.Перевести правильные дробные числа из десятичной системы счисления в двоичную систему счисления c точностью до пяти знаков после запятой.

0,4810 0,5610 0,1910 0,8710 0,8510

0,7710 0,8110 0,4410 0,5210 0,9110

7.2. Перевести правильные дробные числа из десятичной системы счисления в шестнадцатеричную систему счисления c точностью до пяти знаков после запятой.

0,210 0,110 0,710 0,310 0,410

0,610 0,1310 0,910 0,2310 0,4510

Задание 8.

8.1. Перевести смешанные числа из десятичной системы счисления в двоичную систему с точностью до пяти знаков после запятой.

248,7510 14,3810 33,0410 0,74410 48,5510

1,80210 77,77710 10,3610 309,14610 4513,1110

8.2. Перевести смешанные числа из десятичной системы счисления в шестнадцатеричную систему счисления с точностью до пяти знаков после запятой.

45,5710 357,9410 41,6210 107,9910 7,4610

128,06510 273,6610 12,9610 1584,10510 93,1610

Задание 9.

9.1. Перевести числа из двоичной системы счисления в десятичную систему счисления.

1010002 111002 111112 100,1102 10,0012 1,01012

1100101,0012 10110,10112 101,100112 111,001012 10101,0012 1000101,012

9.2. Перевести числа из шестнадцатеричной системы счисления в десятичную систему счисления.

703416 386616 48E16 2А316 А7F616

1E,C516 15,А16 В4,6416 547C,1616 7A14,2816

Задание 10.

10.1. Перевести числа из шестнадцатеричной системы счисления в двоичную, заменив каждую цифру тетрадой.

88Е16 D1616 36А116 750F916 93CD16

127,А16 306,1В16 1239,9716 E6A,A316 9B037В,D416

10.2. Перевести числа из двоичной системы счисления в шестнадцатеричную, заменив каждую цифру тетрадой.

1011 0001 0001,0001 1001₂

0001 1011 1011,1100 1101 1110₂

01 0010 1010 0100,0010 0011 1111₂

1 0001 0110 1101 1001,1001 0101 0111₂

111 1011 0011 1000 0110,1101 1101 1000₂

10.3. Перевести десятичные числа в двоично-десятичный код.

7510 10610 3710 0,9610 6,7510

10,29710 310,8210 647,510 758,3710 98,7610

10.4. Записать двоично-десятичные числа в десятичной системе счисления.

1010 0001 1001,1000 1010_2-10

1101 1101 1110,0110 1011_2-10

101 1001 0011 0110,1011 1001_2-10

11 1011 1011 1101 1111,1010 1011_2-10

1010 0100 1001 1101 1011 0001,1001 0010 0001_2-10

10.5. Перевести числа из десятичной системы счисления в двоичную систему счисления, используя шестнадцатеричную систему в качестве промежуточной системы счисления.

48,0310 85,2710 523,3410 741,9310 103,7510

475,8210 260,1610 320,4210 1779,076310 2028,670210

Арифметические действия