Уравнение прямой, заданной точкой и нормальным вектором
ВЫСШАЯ МАТЕМАТИКА
Методические указания
к решению задач по теме
«Аналитическая геометрия на плоскости и в пространстве»
для студентов всех форм обучения и специальностей
Могилёв 2015
УДК 519.21
ББК 22.1
Рассмотрено и рекомендовано к изданию
на заседании кафедры высшей математики
Протокол № 6 от 18. 12. 2014.
Составители:
старший преподаватель О.А. Шендрикова
старший преподаватель И.В. Юрченко
Рецензент
к.ф.-м. н., доцент С.В. Подолян
УДК 51
ББК 22.1
© Учреждение образования
«Могилевский государственный
университет продовольствия», 2015
Аналитическая геометрия – это раздел математики, который изучает свойства геометрических объектов с помощью алгебраических методов. Основным методом аналитической геометрии является метод координат.
Прямая линия на плоскости
Уравнение прямой, заданной точкой и нормальным вектором
Предположим, что в плоскости выбрана прямоугольная декартова система координат. Положение прямой l на плоскости относительно выбранной системы координат однозначно определено, если известны точка М0(х0; у0), через которую она проходит, и ненулевой вектор  = (А; В) перпендикулярный к этой прямой. Всякий ненулевой вектор перпендикулярный данной прямой называется ее нормальным вектором. Так как все нормальные векторы прямой коллинеарны, то один из них получают из другого умножением на некоторое число не равное нулю, то есть одноименные координаты векторов пропорциональны. Значит, вектор
= (А; В) перпендикулярный к этой прямой. Всякий ненулевой вектор перпендикулярный данной прямой называется ее нормальным вектором. Так как все нормальные векторы прямой коллинеарны, то один из них получают из другого умножением на некоторое число не равное нулю, то есть одноименные координаты векторов пропорциональны. Значит, вектор  выбирается неоднозначно.
выбирается неоднозначно.
Выберем на прямой l произвольную точку М(х; у) и рассмотрим векторы 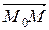 и
и 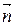 (рисунок 1). Так как векторы перпендикулярны, то их скалярное произведение векторов равно нулю, то есть (
(рисунок 1). Так как векторы перпендикулярны, то их скалярное произведение векторов равно нулю, то есть ( 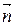 ,
, 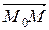 ) = 0. Получили векторное уравнение прямой. Если
) = 0. Получили векторное уравнение прямой. Если  = (А; В), а
= (А; В), а  = (х – х0; у – у0), то, записав векторное уравнение в координатной форме, получим
= (х – х0; у – у0), то, записав векторное уравнение в координатной форме, получим
А(х – х0) + В(у – у0) = 0. (1.1)
Уравнение (1.1) называется уравнением прямой, заданной точкой и нормальным вектором.
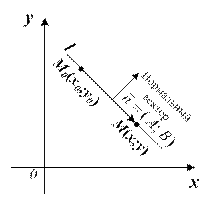
Рисунок 1 – Геометрическая иллюстрация к выводу уравнения (1.1)
Общее уравнение прямой
Рассмотрим уравнение (1.1). Раскрыв скобки в этом уравнении, получим
Ах + Ву + (– Ах0 – Ву0) = 0.
Обозначим – Ах0 – Ву0 = С, тогда уравнение будет иметь вид
Ах + Ву + С = 0. (1.2)
Уравнение (1.2) называется общим уравнением прямой на плоскости с нормальным вектором  = (А, В) (А, В ≠ 0 одновременно).
= (А, В) (А, В ≠ 0 одновременно).
Частные случаи расположения прямой на плоскости:
1) если С = 0, то уравнение (1.2) имеет вид Ах + Ву = 0. Следовательно, прямая проходит через начало координат, то есть О(0, 0)  l;
l;
2) если В = 0 (А ≠ 0), то уравнение имеет вид Ах + С = 0  х =
х = 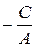 – прямая параллельна оси Оу;
– прямая параллельна оси Оу;
3) если А = 0 (В ≠ 0), то уравнение имеет вид Ву + С = 0 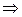 у =
у = 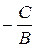 – прямая параллельна оси Ох;
– прямая параллельна оси Ох;
4) если В = С = 0 (А ≠ 0) 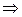 х = 0 – прямая совпадает с осью Оу;
х = 0 – прямая совпадает с осью Оу;
5) если А = С = 0 (В ≠ 0)  у = 0 – прямая совпадает с осью Ох.
у = 0 – прямая совпадает с осью Ох.
Векторное уравнение прямой
Пусть задана точка М0(х0; у0) 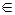 l и ненулевой вектор
l и ненулевой вектор 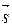 = (т; п) параллельный прямой.
= (т; п) параллельный прямой.
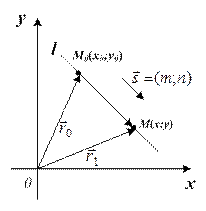
Рисунок 3 – Геометрическая иллюстрация к выводу уравнения (1.5)
Возьмем на прямой l переменную точку М(х; у) (рисунок 3). Векторы 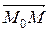 и
и 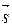 коллинеарны, поэтому при любом положении точки М на прямой будет иметь место равенство
коллинеарны, поэтому при любом положении точки М на прямой будет иметь место равенство
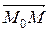 = t
= t 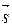 ,
,
где t 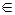 R (t ≠0) – числовой множитель, который может быть любым действительным числом в зависимости от положения точки М на прямой.
R (t ≠0) – числовой множитель, который может быть любым действительным числом в зависимости от положения точки М на прямой.
Пусть 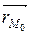 =
= 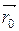 =
= 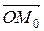 = (х0, у0), а
= (х0, у0), а 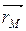 =
= 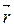 =
= 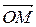 = (х, у). На рисунке 3 видно, что
= (х, у). На рисунке 3 видно, что
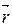 =
= 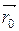 +
+ 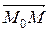 =
= 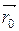 + t
+ t 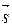 , t
, t 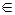 R.
R.
Итак,
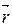 =
= 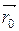 + t
+ t 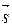 . (1.5)
. (1.5)
Уравнение (1.5) называется векторным параметрическим уравнением прямой.
Решение
Найдем координаты вектора 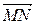 :
:
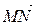 = (хN – xM; yN – yM) = (–1 – 2; 0 – 3) = (–3; –3).
= (хN – xM; yN – yM) = (–1 – 2; 0 – 3) = (–3; –3).
По условию вектор 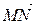 является нормальным вектором искомой прямой.
является нормальным вектором искомой прямой.
Составим уравнение прямой, проходящей через заданную точку М (2; 3) с заданным нормальным вектором 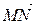 = (–3; –3):
= (–3; –3):
–3(х – 2) –3(у –3) = 0
или
х + у – 5 = 0 – уравнение искомой прямой.
Пример 2.Определить угловой коэффициент k и отрезок b, отсекаемый на оси ординат прямой 2х + 5у – 10 = 0.
Решение
Разрешив уравнение 2х + 5у – 10 = 0 относительно у, получим:
у = – 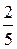 х + 2.
х + 2.
Сравнивая это уравнение с уравнением у = kх + b, находим k = 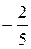 , . b = 2.
, . b = 2.
Пример 3. Найти отрезки, отсекаемые на осях координат прямой
7х + 2у – 14 = 0.
Решение
Разделим обе части уравнения 7х + 2у – 14 = 0 на 14 и перенесем свободный член в правую часть:
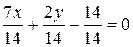 ,
,
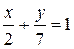 .
.
Сравнивая полученные уравнения с уравнением в отрезках по осям 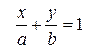 , находим а = 2, b = 7.
, находим а = 2, b = 7.
Пример 4. Написать уравнение прямой, проходящей через точку М (–2, 3) параллельно биссектрисе второго координатного угла.
Решение
Искомая прямая, как и биссектриса второго координатного угла, образует с положительным направлением оси Ох угол φ = 135°, поэтому k = tg135° = – 1. Так как точка М дана, то x0 = – 2, y0 = 3. Тогда уравнение y – y0 = k(x – x0) примет вид
у – 3 = (– 1)∙(х – (– 2)), у – 3 = – х + 2
или
х + у – 1 = 0.
Пример 5. Точки А(3; 5), В(– 1; 3), С(1; – 3) являются вершинами треугольника. Составить уравнение высоты треугольника, проведенной из вершины В.
Решение
Построим данный треугольник (рисунок 7). На высоте возьмем произвольную точку М(х; у) и рассмотрим вектор 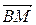 = (х + 1; у – 3), который является перпендикулярным вектору
= (х + 1; у – 3), который является перпендикулярным вектору 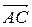 = (1 – 3; – 3 – 5) = (– 2; – 8). Значит, их скалярное произведение равно нулю:
= (1 – 3; – 3 – 5) = (– 2; – 8). Значит, их скалярное произведение равно нулю: 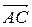 ∙
∙ 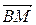 = 0. В координатной форме имеем
= 0. В координатной форме имеем
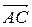 ∙
∙ 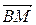 = – 2∙(х + 1) – 8∙(у – 3) = 0,
= – 2∙(х + 1) – 8∙(у – 3) = 0,
или
(х + 1) + 4∙(у – 3) = 0,
Х + 4у – 11 = 0 – уравнение высоты BМ.
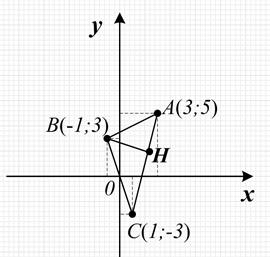
Рисунок 7 – Треугольник АВС
Пример 6. Даны вершина С(– 1; 3) прямого угла равнобедренного прямоугольного треугольника и уравнение его гипотенузы 3х – 4у – 12 = 0. Составить уравнения катетов.
Решение
Из уравнения гипотенузы выразим у и найдем ее угловой коэффициент:
3х – 4у – 12 = 0,
– 4у = – 3х + 12,
у = 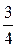 х – 3.
х – 3.
Следовательно, k1 = 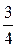 .
.
Катеты равнобедренного прямоугольного треугольника наклонены к гипотенузе под углом 45°. По формуле tgφ = 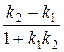 найдем угловые коэффициенты катетов:
найдем угловые коэффициенты катетов:
tg45° = 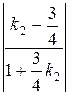 ,
,
±1 = 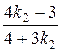 .
.
Если 1 = 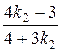 , то k2 = 7.
, то k2 = 7.
Если – 1 = 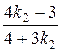 , то k2 = –
, то k2 = – 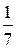 .
.
Зная координаты точки С(– 1; 3), принадлежащей двум катетам, получим их уравнения:
у – 3 = 7(х + 1), 7х – у + 10 = 0.
у – 3 = – 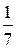 (х + 1), х + 7у – 20 = 0.
(х + 1), х + 7у – 20 = 0.
Пример 7. Найти уравнения прямых, которые параллельны прямой 12х + 5у – 7 = 0 и удалены от нее на расстояние равное трем.
Решение
Для любой точки прямой М(х; у) не лежащей на прямой 12х + 5у – 7 = 0, по формуле d = 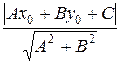 должно выполняться равенство
должно выполняться равенство
3 = 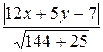 ,
,
или
|12х + 5у – 7| = 3∙13,
|12х + 5у – 7| = 39.
Следовательно,
12х + 5у – 7 = 39 или 12х + 5у – 7 = – 39.
Таким образом, получим уравнения прямых
12х + 5у – 46 = 0 и 12х + 5у + 32 = 0.
Пример 8. Даны уравнения двух смежных сторон АВ и АD параллелограмма и точка N пересечения его диагоналей. Найти уравнения двух других сторон параллелограмма, если N(3; 3), х + у – 1 = 0 (АВ), 3х – у + 5 = 0 (АD).
Решение
Найдем координаты точки пересечения прямых АВ и АD, решив систему уравнений
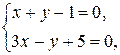
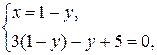
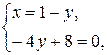
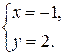
Получили точку А(– 1; 2).
Найдем координаты точки С, применив формулы деления отрезка пополам (так как точка N – середина диагонали АС).
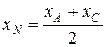 ,
, 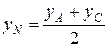 .
.
Таким образом, имеем
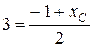 ,
, 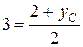 ,
,
откуда хС = 7, уС = 4, то есть С(7; 4).
Так как четырехугольник АВСD – параллелограмм, то АВ || СD и AD || CB и  ↑↓
↑↓ 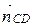 ,
, 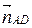 ↑↓
↑↓ 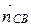 . Значит, можно считать, что
. Значит, можно считать, что 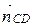 =
= 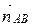 = (1; 1),
= (1; 1), 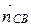 =
= 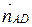 = (3; – 1). Запишем уравнения сторон СD и СВ, используя уравнение (1.1). Имеем
= (3; – 1). Запишем уравнения сторон СD и СВ, используя уравнение (1.1). Имеем
3(х – 7) – (у – 4) = 0, 3х – у – 17 = 0 (СВ),
(х – 7) + (у – 4) = 0, х + у – 11 = 0 (СD).
Вопросы для самопроверки
1 Записать общее уравнение прямой на плоскости.
2 Каков геометрический смысл коэффициентов при х и у в общем уравнении прямой?
3 Записать уравнение прямой на плоскости, проходящей через точку М0(х0; у0) перпендикулярно вектору 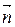 = (А; В).
= (А; В).
4 Записать каноническое уравнение прямой на плоскости и указать геометрический смысл входящих в него параметров.
5 Записать параметрические уравнения прямой на плоскости.
6 Записать уравнение прямой с угловым коэффициентом и указать геометрический смысл входящих в него параметров.
7 Записать уравнение прямой, проходящей через точку М0(х0; у0) и образующей с осью абсцисс угол, тангенс которого равен k.
8 Записать уравнение прямой, проходящей через точки М1(х1; у1) и М2(х2; у2).
9 Записать уравнение прямой в отрезках по осям и указать геометрический смысл входящих в него параметров.
10 Записать формулы, по которым можно найти угол φ между прямыми.
11 Записать условие параллельности и условие перпендикулярности двух прямых, заданных:
а) общими уравнениями;
б) каноническими уравнениями;
в) уравнениями с угловыми коэффициентами.
12 Чему равно расстояние от точки М0(х0; у0) до прямой Ах + Ву + С = 0?
Задачи для самостоятельного решения
1Составить уравнение прямой, проходящей через точку М(– 2; 2) параллельно вектору:
а) 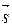 = (– 1; 1);
= (– 1; 1);
б) 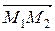 , если М1(2; – 5), М2(3; 1).
, если М1(2; – 5), М2(3; 1).
(Ответ: а) х + у = 0; б) 6х – у + 14 = 0)
2Найти уравнение прямой, проходящей через точку М(1; 2) с нормальным вектором 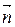 = (3; – 4). (Ответ: 3х – 4у + 5= 0)
= (3; – 4). (Ответ: 3х – 4у + 5= 0)
3При каком значении С точка М(3;– 2) принадлежит прямой 2х + 5у + С = 0. (Ответ: С = 4)
4Задана прямая 2х + 3у + 4 = 0. Составить уравнение прямой, проходящей через точку М(2; 1):
а) параллельно данной прямой;
б) перпендикулярно данной прямой;
в) под углом 45° к данной прямой.
(Ответ: а) 2х + 3у – 7 = 0; б) 3х – 2у – 4 = 0; в) х – 5у + 3 = 0, 5х + у – 11 = 0)
5Найти уравнение прямой, проходящей через точку М(– 4; 10) и отсекающей отрезки равной длины на осях координат. (Ответ: х + у – 6 = 0)
6Дан треугольник с вершинами Р(3; 1), Q(– 3; – 1), R(5; 12). Найти уравнение медианы, проведенной из вершины R, и вычислить ее длину. (Ответ: 12х + 5у = 0, d = 13)
7Даны две вершины А(– 2; 1) и В(3; – 4) треугольника и точка N(5; – 1) пересечения его высот. Найти уравнения всех сторон треугольника. (Ответ: х + у + 1 = 0, 7х – 2у – 29 = 0, 2х + 3у + 1 = 0)
8Найти уравнение прямой, проходящей через точку А(1; – 2) и точку пересечения прямых 2х + 3у – 4 = 0 и 3х – 5у + 13 = 0. (Ответ: 2х + у = 0)
9Найти проекцию точки А(– 8; 12) на прямую, проходящую через точки М1(2; – 3) и М2(– 5; 1). (Ответ: (– 12; 5))
10Найти точку В, симметричную точке А(8; 12) относительно прямой х – 2у + 6 = 0. (Ответ: В(12; 4))
11Через точку А(2; 5) провести прямые, которые находятся на одинаковом расстоянии от точек М1(– 1; 2) и М2(5; 4). (Ответ: х – 2 = 0, х – 3у + 13 = 0)
12Найти угол между прямыми:
а) х + 5у – 3 = 0, 2х – 3у + 4 = 0;
б) х + 2у – 3 = 0, у = – 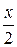 –
– 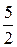 ;
;
в) у = 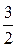 х + 1, у =
х + 1, у = 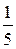 х – 3.
х – 3.
(Ответ: а) 45°; б) 0°; в) 45°)
13Определить, при каком значении параметра α прямые
(α – 1)х – 2αу + 5 = 0 и αх + 4αу – 6 = 0:
а) параллельны;
б) совпадают;
в) взаимно перпендикулярны.
(Ответ: а) α = 2; б) ни при каком α; в) α = 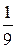 )
)
14Две стороны квадрата лежат на прямых, заданных уравнениями 5х – 12у – 65 = 0 и 5х – 12у + 26 = 0. Найти площадь квадрата. (Ответ: 49)
15Доказать, что прямые 3х – 4у + 10 = 0 и 6х – 8у + 15 = 0 и найти расстояние между ними. (Ответ: 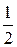 )
)
Линии второго порядка
Окружность
Окружностью называют множество всех точек плоскости, равноудаленных от некоторой фиксированной точки, называемой центром окружности.
Если R – радиус окружности, а точка М(х0; у0) – центр окружности, то ее уравнение имеет вид
(х – х0)2 + (у – у0)2 = R2.
Если центр окружности совпадает с началом координат, то ее уравнение записывается в виде
х2 + у2 = R2.
Эллипс
Эллипсом называют множество всех точек плоскости, для которых сумма расстояний от двух данных точек F1 и F2, называемых фокусами, есть величина постоянная, равная 2а, и большая, чем расстояние между фокусами 2с (2а > 2с).
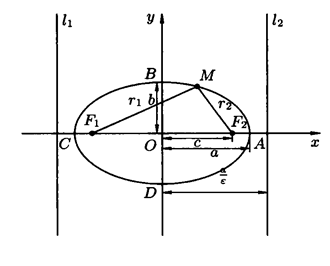
Рисунок 8 – Эллипс
Каноническое уравнение эллипса:
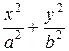 = 1.
= 1.
Начало координат О(0; 0) является центром симметрии эллипса, а оси координат – осями симметрии эллипса. Точки А(а; 0), С(– а; 0), В(0; b), D(0; – b) называются вершинами эллипса (рисунок 8).
b2 = а2 – с2, а = ОА – большая полуось, b = ОВ – малая полуось. Координаты фокусов F1(– c; 0), F2(c; 0).
Отношение
ε = 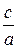 < 1
< 1
называется эксцентриситетом эллипса.
Прямые х = ± 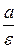 называются директрисами эллипса.
называются директрисами эллипса.
Если а < b, то фокусы эллипса находятся на оси Оу, с2 = b2 – а2, ε = 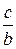 .
.
Гипербола
Гиперболой называют множество всех точек плоскости, для которых модуль разности расстояний от двух данных точек F1 и F2, называемых фокусами, есть величина постоянная, равная 2а, и меньшая, чем расстояние между фокусами 2с (2а < 2с).
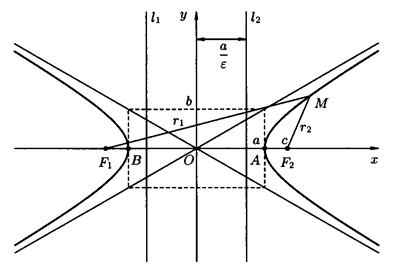
Рисунок 9 – Гипербола
Каноническое уравнение гиперболы:
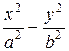 = 1.
= 1.
Начало координат О(0; 0) является центром симметрии гиперболы, а оси координат – осями гиперболы. Точки А(а; 0), В(– а; 0) называются вершинами гиперболы (рисунок 9).
b2 = с2 – а2, а – действительная полуось, b – мнимая полуось. Координаты фокусов F1(– c; 0), F2(c; 0).
Отношение
ε = 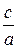 > 1
> 1
называется эксцентриситетом гиперболы.
Прямые у = ± 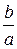 х называются асимптотами гиперболы.
х называются асимптотами гиперболы.
Гипербола, у которой a = b, называется равносторонней.
Уравнение
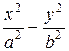 = – 1
= – 1
также является уравнением гиперболы, но действительной осью этой гиперболы служит отрезок оси Оу длиной 2b.
Парабола
Параболой называют множество всех точек плоскости, каждая из которых находится на одинаковом расстоянии от данной точки F, называемой фокусом, и от данной прямой, называемой директрисой и не проходящей через фокус.
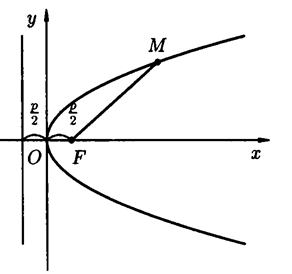
Рисунок 10 – Парабола
Каноническое уравнение параболы, симметричной относительно оси Ох и проходящей через начало координат, имеет вид
у2 = 2рх,
где р – расстояние от фокуса параболы F( 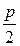 ; 0) до ее директрисы х = –
; 0) до ее директрисы х = – 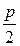 (рисунок 10).
(рисунок 10).
Каноническое уравнение параболы, симметричной относительно оси Оу с вершиной в начале координат, имеет вид
х2 = 2ру.
В этом случае F(0; 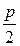 ) – фокус, у = –
) – фокус, у = – 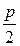 – уравнение директрисы.
– уравнение директрисы.
Пример 1. Составить уравнение окружности, если точки М1(3; 2), М2(– 1; 6) – концы диаметра окружности.
Решение
Найдем координаты центра окружности по формулам деления отрезка пополам:
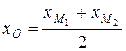 =
= 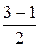 = 1,
= 1,
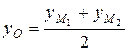 =
= 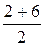 = 4.
= 4.
Вычислим радиус окружности:
ОМ1 = R = 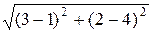 =
= 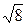 = 2
= 2 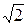 .
.
Тогда уравнение окружности:
(х – 1)2 + (у – 4)2 = 8.
Пример 2. Составить каноническое уравнение эллипса, если известно, что его большая полуось а = 12, а эксцентриситет ε = 0,5.
Решение
Известно, что ε = 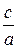 . Следовательно,
. Следовательно,
с = аε = 12∙0,5 = 6.
Используя соотношение b2 = а2 – с2, получим
b2 = 144 – 36 = 108.
Таким образом, искомое уравнение эллипса имеет вид
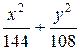 = 1.
= 1.
Пример 3. Составить уравнение гиперболы, если известно, что она проходит через точку М(9; 8), а асимптоты заданы уравнениями у = ± 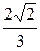 х. Найти эксцентриситет гиперболы.
х. Найти эксцентриситет гиперболы.
Решение
Из уравнений асимптот гиперболы находим 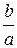 =
= 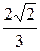 , или b =
, или b = 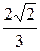 а.
а.
Подставив в каноническое уравнение гиперболы полученное выражение для b, имеем
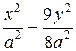 = 1.
= 1.
Точка М(9; 8) принадлежит гиперболе, следовательно, ее координаты удовлетворяют уравнению гиперболы. Значит
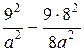 = 1,
= 1,
81 – 72 = а2,
а2 = 9, а = 3.
Тогда b = 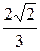 а =
а = 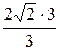 =
= 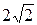 . Искомое уравнение гиперболы имеет вид
. Искомое уравнение гиперболы имеет вид
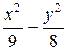 = 1.
= 1.
Найдем эксцентриситет гиперболы:
ε = 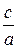 =
= 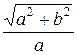 =
= 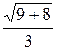 =
= 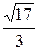 .
.
Пример 4. Составить уравнение параболы, если известно, что:
а) фокус параболы F(5; 0), а ее директрисой является ось ординат;
б) парабола симметрична относительно оси Оу и проходит через точки О(0; 0) и М(6; – 2).
Решение
а) По условию р = 5 и вершина параболы имеет координаты (2,5; 0), то, используя уравнение у2 = 2р(х – х0), получим
у2 = 10(х – 2,5),
у2 = 10х – 25.
б) Запишем уравнение параболы в общем виде: х2 = 2ру.
Точка М(6; – 2) удовлетворяет уравнению параболы, то есть
36 = 2р∙(– 2),
– 4р = 36,
р = – 9.
Тогда уравнение параболы имеет вид
х2 = – 18у.
Вопросы для самопроверки
1 Какая линия называется эллипсом? Какие точки называются фокусами эллипса?
2 Записать каноническое уравнение эллипса.
3 Для эллипса, заданного каноническим уравнением 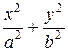 = 1, указать оси симметрии и вершины.
= 1, указать оси симметрии и вершины.
4 Какая ось эллипса называется большой осью и какая – малой?
5 Пусть 2а и 2b – соответственно большая и малая оси эллипса, а 2с – расстояние между его фокусами. Какова зависимость между а, b и с?
6 Какая линия называется гиперболой? Какие точки называются фокусами гиперболы?
7 Записать каноническое уравнение гиперболы.
8 Для гиперболы, заданной каноническим уравнением 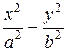 = 1, указать оси симметрии и вершины.
= 1, указать оси симметрии и вершины.
9 Указать вершины гиперболы, заданной каноническим уравнением 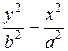 = 1.
= 1.
10 Что является действительной осью гиперболы 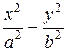 = 1?
= 1?
11 Что является мнимой осью гиперболы 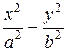 = 1?
= 1?
12 Пусть 2а и 2b – соответственно действительная и мнимая оси гиперболы, а 2с – расстояние между ее фокусами. Какова зависимость между а, b и с?
13 Записать уравнения асимптот гиперболы 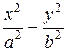 = 1.
= 1.
14 Какая линия называется параболой? Какая точка называется фокусом параболы и какая прямая – директрисой, заданной уравнением у2 = 2рх?
15 Записать каноническое уравнение параболы.
16 Какая точка называется вершиной параболы?
17 Что называется эксцентриситетом эллипса?
18 Чему равен эксцентриситет ε эллипса, заданного уравнением 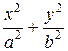 = 1, где а > b?
= 1, где а > b?
19 Что называется эксцентриситетом гиперболы?
20 Чему равен эксцентриситет ε гиперболы, заданной уравнением 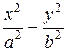 = 1?
= 1?
Задачи для самостоятельного решения
1Составить уравнение окружности, которая имеет центр в точке М(2; 3) и касается прямой х – 2у + 1 = 0. (Ответ: (х – 2)2 + (у – 3)2 = 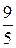 )
)
2Составить уравнение окружности, которая проходит через точки А(5; 0) и В(1; 4), если ее центр лежит на прямой х + у – 3 = 0.
(Ответ: (х – 2)2 + (у – 1)2 = 10)
3Составить уравнение хорды окружности х2 + у2 = 49, которая делится точкой А(1; 2) пополам. (Ответ: х + 2у – 5 = 0)
4Составить каноническое уравнение эллипса, проходящего через точки М( 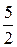 ;
; 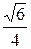 ) и N(–2;
) и N(–2; 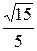 ). (Ответ:
). (Ответ: 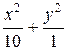 = 1)
= 1)
5Составить уравнение геометрического множества точек плоскости, расстояние от которых до точки А(0; 1) в два раза меньше расстояния до прямой у – 4 = 0. (Ответ: 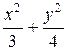 = 1)
= 1)
6Составить каноническое уравнение эллипса, если известно, что малая полуось равна 6, а расстояние между фокусами равно 16. (Ответ: 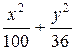 = 1)
= 1)
7Эллипс касается оси абсцисс в вершине А(4; 0) и оси ординат в вершине В(0; – 3).Составить уравнение эллипса. (Ответ: 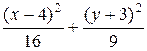 = 1)
= 1)
8Найти эксцентриситет эллипса, если известно, что:
а) большая ось втрое больше малой;
б) оси относятся как 5:3.
(Ответ: а) 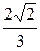 ; б) 0,8)
; б) 0,8)
9Составить каноническое уравнение эллипса, если известно, что:
а) малая полуось равна 6, эксцентриситет равен 0,8;
б) расстояние между фокусами равно 6, эксцентриситет равен 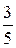 ;
;
в) сумма полуосей равна 10, расстояние между фокусами равно 4 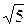 .
.
(Ответ: а) 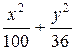 = 1; б)
= 1; б) 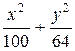 = 1; в)
= 1; в) 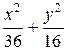 = 1)
= 1)
10Составить каноническое уравнение гиперболы, действительная ось которой равна 48, а эксцентриситет равен 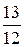 . (Ответ:
. (Ответ: 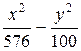 = 1)
= 1)
11Составить уравнение гиперболы, проходящей через точку М(24; 5), если ее асимптоты заданы уравнениями у = ± 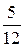 х. (Ответ:
х. (Ответ: 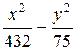 = 1)
= 1)
12Составить уравнение гиперболы, вершины которой находятся в фокусах, а фокусы – в вершинах эллипса 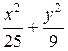 = 1. (Ответ:
= 1. (Ответ: 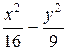 = 1)
= 1)
13Найти уравнение параболы и ее директрисы, если известно, что парабола проходит через точку пересечения прямой х + у = 0 и окружности х2 + у2 – 4х = 0 и симметрична относительно оси Оу. (Ответ: х2 = – 2у; у = 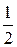 )
)
14Составить уравнение параболы, если известно, что ее фокус находится в точке пересечения прямой 4х – 3у – 4 = 0 с осью Ох. (Ответ: у2 = 4х)
15Привести уравнения линий второго порядка к каноническому виду, определить их тип и расположение на плоскости:
а) 4х2 + 9у2 – 40х + 36у + 100 = 0;
б) 16х2 – 9у2 – 64х – 18у + 199 = 0;
в) 5х2 + 9у2 – 30х + 18у + 9 = 0;
г) 3х2 – 4у2 – 12х + 24 = 0;
д) у2 + 2у + 4х – 11 = 0.
(Ответ: а) 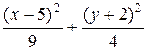 = 1 – эллипс; б)
= 1 – эллипс; б) 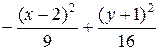 = 1 – гипербола; в)
= 1 – гипербола; в) 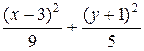 = 1 – эллипс; г)
= 1 – эллипс; г) 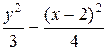 = 1 – гипербола; д) (у + 1)2 = – (х – 3) – парабола)
= 1 – гипербола; д) (у + 1)2 = – (х – 3) – парабола)
Угол между плоскостями
Пусть даны две плоскости
А1х + В1у + С1z + D1 = 0,
А2х + В2у + С2z + D2 = 0.
За угол между плоскостями принимаем угол φ между любыми двумя перпендикулярными к ним векторами (что дает два угла, острый и тупой, дополняющих друг друга до π). Так как нормальные векторы плоскостей 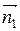 = (А1, В1, С1) и
= (А1, В1, С1) и 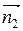 = (А2, В2, С2) перпендикулярны им, то получаем
= (А2, В2, С2) перпендикулярны им, то получаем
cosφ = 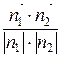
или
cosφ = 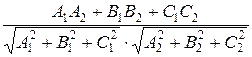 .
.
Решение
Согласно уравнению (3.1) получаем
3(х + 1) – (у – 2) + 2(z – 7) = 0,
3х – у + 2z – 9 = 0.
Пример 2.Составить уравнение плоскости, проходящей через точку М(2; – 3; – 7) параллельно плоскости 2х – 6у – 3z + 5 = 0.
Решение
Вектор  = (2; – 6; – 3) перпендикулярный к плоскости перпендикулярен и к параллельной плоскости. Значит, искомая плоскость проходит через точку М(2; – 3; – 7) перпендикулярно вектору
= (2; – 6; – 3) перпендикулярный к плоскости перпендикулярен и к параллельной плоскости. Значит, искомая плоскость проходит через точку М(2; – 3; – 7) перпендикулярно вектору  = (2; – 6; – 3). Найдем уравнение плоскости по формуле (3.1):
= (2; – 6; – 3). Найдем уравнение плоскости по формуле (3.1):
2(х – 2) – 6(у + 3) – 3(z + 7) = 0,
2х – 6у – 3z – 43 = 0.
Пример 3.Найти уравнение плоскости, проходящей через точки М1(2; 3; – 1) и М2(1; 5; 3)перпендикулярно к плоскости 3х – у + 3z + 15 = 0.
Решение
Вектор  = (3; – 1; 3) перпендикулярный к заданной плоскости будет параллелен искомой плоскости. Таким образом, плоскость проходит через точки М1 и М2 параллельно вектору
= (3; – 1; 3) перпендикулярный к заданной плоскости будет параллелен искомой плоскости. Таким образом, плоскость проходит через точки М1 и М2 параллельно вектору  .
.
Пусть М(x; y; z) произвольная точка плоскости, тогда векторы 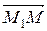 = (х – 2; у – 3; z + 1),
= (х – 2; у – 3; z + 1), 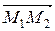 = (– 1; 2; 4),
= (– 1; 2; 4),  = (3; – 1; 3) компланарны, значит их смешанное произведение равно нулю:
= (3; – 1; 3) компланарны, значит их смешанное произведение равно нулю:
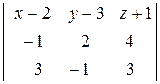 = 0.
= 0.
Вычислим определитель разложением по элементам первой строки:
(х – 2) 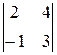 – (у – 3)
– (у – 3) 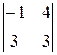 + (z + 1)
+ (z + 1) 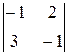 = 0,
= 0,
10(х – 2) – (– 15)(у – 3) + (– 5)(z + 1) = 0,
2(х – 2) + 3(у – 3) – (z + 1) = 0,
2х + 3у – z – 14 = 0 – уравнение плоскости.
Пример 4.Составить уравнение плоскости, проходящей через начало координат перпендикулярно к плоскостям 2х – у + 5z + 3 = 0 и х + 3у – z – 7 = 0.
Решение
Пусть  – нормальный вектор искомой плоскости. По условию плоскость перпендикулярна данным плоскостям, значит
– нормальный вектор искомой плоскости. По условию плоскость перпендикулярна данным плоскостям, значит 
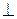
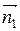 и
и 
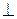
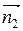 , где
, где 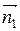 = (2; – 1; 5),
= (2; – 1; 5), 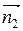 = (1; 3; – 1). Значит, в качестве вектора
= (1; 3; – 1). Значит, в качестве вектора  можно взять векторное произведение векторов
можно взять векторное произведение векторов 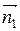 и
и 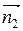 , то есть
, то есть  =
= 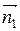 ×
× 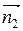 .
.
 =
= 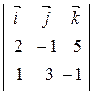 = – 14
= – 14  + 7
+ 7  + 7
+ 7  .
.
Подставив координаты вектора  в уравнение плоскости, проходящей через начало координат Ах + Ву + Сz = 0, получим
в уравнение плоскости, проходящей через начало координат Ах + Ву + Сz = 0, получим
– 14х + 7у + 7z = 0,
или
2х – у – z = 0.
Вопросы для самопроверки
1 Записать общее уравнение плоскости.
2 Каков геометрический смысл коэффициентов при х, у, z в общем уравнении плоскости?
3 Записать уравнение плоскости, проходящей через точку М0(x0; y0; z0) перпендикулярно к вектору 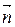 = (А; В; С).
= (А; В; С).
4 Записать уравнение плоскости в отрезках по осям и указать геометрический смысл входящих в него параметров.
5 Записать уравнение плоскости, проходящей через точки М1(х1; у1; z1), М2(х2; у2; z2)
