Авторегрессионные модели и их моделирование

Рассмотренные ранее модели авторегрессии содержали в правой части наряду с лаговыми зависимыми переменными ( 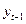, 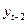и т.п.) независимые переменные ( 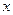). Авторегрессионная модель, в которой отсутствуют независимые переменные и 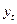рассматривается как линейная функция только предыдущих своих значений, представляет собой авторегрессионный процесс:

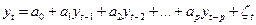. (8.6)

В зависимости от того, сколько предыдущих уровней временного ряда включено в уравнение (8.6), авторегрессионный процесс может быть разного порядка. Если текущее значение уровня динамического ряда ( 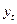) рассматривается как линейная функция от одного предыдущего значения, то имеем дело с авторегрессионным процессом первого порядка, что обычно в англоязычной литературе обозначается как AR(1):

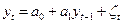. (8.7)

Увеличивая число лаговых переменных в модели (8.7), получим авторегрессионный процесс более высокого порядка. Например, процесс AR(3) сводится к уравнению:

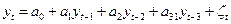(8.8)

и отражает авторегрессионный процесс третьего порядка.

Среди моделей для стационарных временных рядов широкое распространение имеют модели скользящей средней.

Для стационарного ряда моделируемый уровень временного ряда можно представить как линейную функцию прошлых ошибок, т.е. разностей между прошлыми фактическими и теоретическими уровнями:

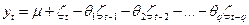, (8.9)

где 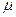- константа;

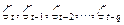- белый шум в текущий и предыдущий период времени;

.

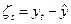Термин «скользящая средняя», используемый здесь, не синоним скользящей средней как методу сглаживания уровней динамического ряда.

В модели (8.9) уровень динамического ряда рассматривается как сумма константы ( 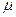) и скользящей средней между текущим и предыдущими значениями белого шума (случайных отклонений).

Обозначим скользящую среднюю модели (8.9) через :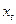

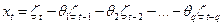. (8.10)

Уравнение (8.10) принято называть процессом скользящего среднего порядка 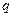и обозначать как MA(q) (от английского moving average). Порядок скользящей средней определяется числом учитываемых в модели предыдущих значений случайных отклонений. Так, МА(2) можно записать как 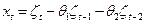, а модель уровня динамического ряда с использованием МА(2) будет иметь вид

.

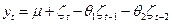Соответственно модель уровня ряда с использованием МА(1) примет выражение

.

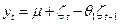При 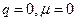получаем процесс белого шума.

Временные ряды с использованием процесса скользящего среднего могут иметь место, когда уровни динамического ряда характеризуются случайной колеблемостью.

Соединение в одной модели авторегрессионного процесса AR и модели скользящего среднего МА приводит к модели авторегрессионного процесса со скользящими средними в остатках (от английского ARMA – Auto Reqressiv – Moving Average):

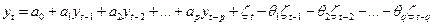. (8.11)

В модели (8.11) в качестве объясняющих переменных рассматриваются лаговые значения зависимой переменной с 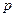интервалами сдвига и скользящие средние порядка 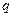для остатков авторегрессии. Иными словами, модель включает в себя AR( 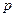) и МА( 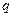). Ее принято обозначать ARMA( 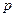, 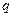). Например, ARMA(3,2) имеет вид

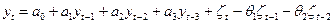. (8.12)

При практической реализации моделей ARMA наиболее сложным является выбор числа лагов 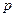и .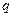

Для получения стационарного ряда могут рассчитываться разности уровней временного ряда ( 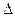) разного порядка (d). Модель, в которой соединены нахождение последовательных разностей временного ряда порядка d и ARMA – модель порядка ( 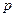, 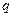), получила название авторегрессионной интегрированной модели скользящего среднего – ARIМА (Autoregressiv Integrated Moving Average).

Модель ARIМА обладает тремя параметрами: 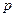– порядок авторегрессии (AR); d – порядок последовательных разностей уровней временных рядов, обеспечивающих стационарность ряда; 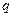– порядок скользящей средней (MA).

В общем виде модель ARIМА ( 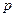,d, 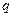) выражается формулой

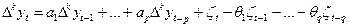, (8.13)

где 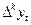- -я последовательная разность уровней 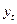, т.е. ;

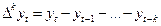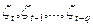- нормально распределенные случайные величины с нулевым математическим ожиданием и постоянной дисперсией.

Контрольные вопросы:

1. Какой вид имеет модель с распределенными лагами?

2. Каков вид авторегрессионной модели с распределенными лагами?

3. Как интерпретируются параметры модели с распределенными лагами?

4. В каких случаях оценка параметров модели с распределенными лагами может быть дана методом наименьших квадратов?

5. Что такое модели авторегрессии?

6. Для чего используются инструментальные переменные?

7. Что такое авторегрессионные процессы со скользящими средними в остатках?

8. Каков вид модели ARMA (3, 2)?

ТЕМА 9. СИСТЕМЫ ЛИНЕЙНЫХ

ОДНОВРЕМЕННЫХ УРАВНЕНИЙ

План лекции

1. Структурная и приведенная формы моделей.

2. Проблема идентификации.

3. Оценивание параметров структурной модели.

Введение

Одной из причин коррелированности регрессоров со случайными членами могут служить факторы, действующие одновременно на сами регрессовы и на объясняемые переменные при фиксированных значениях регрессоров. В рассматриваемой экономической ситуации значения объясняемых переменных и регрессоров формируются одновременно под воздействием некоторых внешних факторов. Это означает, что рассматриваемую модель следует дополнять уравнениями, в которых объясняемыми переменными выступали бы сами регрессоры. Таким образом приходится рассматривать системы одновременных или регрессионных уравнений.