Понятие об авторегрессионных моделях

и моделях скользящей средней

До сих пор мы рассматривали модели временного ряда вида (7.9), в которых в качестве регрессора выступала переменная t-«время». В эконометрике достаточно широкое распространение получили и другие регрессионные модели, в которых регрессорами выступают лаговые перемены, т.е. переменные, влияние которых в эконометрической модели характеризуется некоторым запаздыванием. Причем представленные в моделях объясняющие переменные являются случайными величинами (см. подробнее в теме 8).

Авторегрессионная модель q-го порядка (или модель AR(p)) имеет вид:

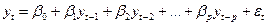
где (t = 1,2,…,n), b₀ b₁,…, b_p – некоторые константы.

Если исследуемый процесс у_t в момент t определяется его значениями только в предшествующий период t – 1, то рассматривают авторегрессионную модель 1-го порядка (модель AR(p)):

у_t = b₀ + b₁у_t-1 + e_t (t = 1,2,…,n)

Наряду с авторегрессионными моделями временных рядов в эконометрике рассматриваются также модели скользящей средней (не путать с аналогичным термином, используемым в технике сглаживания рядов), в которой, моделируемая величина задается линейной функцией от возмущений в предыдущие моменты времени.

Модель скользящей средней q-го порядка (или модель МA(q)) имеет вид:

у_t = e_t + g₁e_t-1 + g₂e_t-2 +…+ g_qe_t-q.

В эконометрике используются комбинированные модели временных рядов AR и МА.

Контрольные вопросы:

1. Что представляет собой временной ряд?

2. Какие составляющие выделяют при исследовании временного ряда?

3. Каков общий вид мультипликативной, аддитивной моделей временного ряда?

4. Каким требованиям отвечают стационарные временные ряды?

5. Что такое выборочный коэффициент автокорреляции?

6. Дайте определения автокорреляционной функции и коррелограммы временного ряда.

7. С помощью какого критерия определяют автокорреляцию остатков?

8. Как провести точечный и интервальный прогноз исследуемого показателя?

9. Какова модель авторегрессии?

10. Каков вид модели скользящей средней q-го порядка?

ТЕМА 8: МОДЕЛИ С ЛАГОВЫМИ ПЕРЕМЕННЫМИ

План лекции

1. Модели с распределенными лагами.

2. Модели авторегрессии.

3. Авторегрессионные модели и их моделирование.

Введение

В моделях временных рядов зависимая переменная 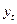может быть связана не только со значениями объясняемых переменных 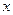в момент времени 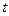, но и с их значениями в предыдущие моменты времени. Так, например, потребление товаров длительного пользования зачастую зависит не только от доходов текущего, но предыдущих периодов. Аналогично величина основных производственных фондов зависит от размера инвестиций не только текущего года, но и предыдущих лет. В этом случае строятся модели с лаговыми объясняющими переменными. Например,

,

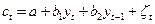где 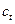- потребление в период времени ;

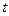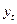- доход в период времени ;

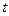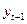- доход в предыдущий период .

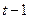В данной модели лаговой является переменная у_t-1, т.е. доход за предыдущий период времени. Возможна ситуация, когда объясняющая переменная 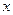влияет на результат 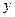не сразу же, а с определенным запаздыванием во времени, превышающим один временной интервал. Так, выпуск специалистов высшей квалификации зависит от приема в вузы четырех – пятилетней давности.

Объясняющие переменные, взятые в модели регрессии с запаздыванием во времени, называются лаговыми переменными. Величина интервала запаздывания называется лагом. Так в модели 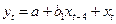лаговая переменная взята с лагом, равным 4.

Вместе с тем в правой части модели лаговой может быть и зависимая переменная.

Модели регрессии по временным рядам с лаговыми переменными принято называть динамическими моделями. Их можно подразделить на три класса:

1) модели с лаговыми объясняющими переменными, или, иначе, модели с распределенными лагами:

;

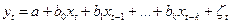2) модели с лаговыми зависимыми переменными – модели авторегрессии:

;

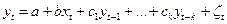3) модели с лаговыми зависимыми и независимыми переменными, т.е. авторегрессионные модели с распределенными лагами:

.

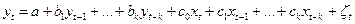Выбор величины лага и количества лагов проводится обычно экспериментально: строятся модели с разным числом лагов и их величиной и изучается значимость коэффициентов регрессии при лаговых переменных; останавливаются на модели, для которой все коэффициенты регрессии при лаговых переменных будут статистически значимыми по 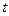-критерию Стьюдента.