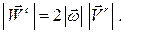Вычисление ускорения Кориолиса
Ускорение Кориолиса возникает в тех случаях, когда точка движется по отношению к некоторому телу, которое, в свою очередь, вращается по отношению к некоторой системе отсчёта. Ось вращения тела может перемещаться и поворачиваться по отношению к выбранной неподвижной системе отсчета. Положение оси вращения, направление и быстрота вращения задаются вектором угловой скорости:
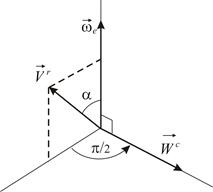 |
| Рис. 3.1 |
вектор угловой скорости тела 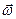 расположен вдоль оси вращения и направлен в ту сторону, откуда вращение тела видно происходящим против хода часовой стрелки.
расположен вдоль оси вращения и направлен в ту сторону, откуда вращение тела видно происходящим против хода часовой стрелки.
Вектор ускорения Кориолиса перпендикулярен плоскости, содержащей вектор угловой скорости подвижной системы отсчета и вектор относительной скорости точки, причем направлен в ту сторону, откуда кратчайший поворот от вектора 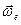 к вектору
к вектору 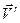 виден против хода часовой стрелки (Рис. 3.1). Модуль ускорения Кориолиса определяется по формуле:
виден против хода часовой стрелки (Рис. 3.1). Модуль ускорения Кориолиса определяется по формуле:
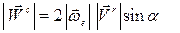 где
где 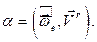
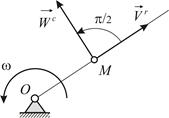 |
| Рис. 3.2 |
Напомним случаи обращения в нуль ускорения Кориолиса:
1. 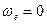 , т.е. подвижная система отсчета движется поступательно;
, т.е. подвижная система отсчета движется поступательно;
2. вектор угловой скорости подвижной системы отсчета коллинеарен вектору относительной скорости точки;
3. в моменты времени, когда относительная скорость точки обращается в нуль.
Для определения направления ускорения Кориолиса можно использовать правило Жуковского (Рис.3.1):
для определения направления ускорения Кориолиса необходимо проекцию вектора относительной скорости на плоскость, перпендикулярную вектору угловой скорости подвижной системы отсчета, повернуть в сторону вращения на угол 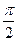 .
.
Особенно удобно применять правило Жуковского в тех часто встречающихся случаях, когда вектор относительной скорости перпендикулярен вектору угловой скорости подвижной системы отсчета (Рис. 3.2).
Пример 3.1
Треугольная пластина 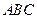 вращается вокруг стороны
вращается вокруг стороны 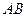 с угловой скоростью
с угловой скоростью 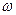 , Если смотреть от
, Если смотреть от  к
к  , вращение видно происходящим против хода часовой стрелки. Вдоль стороны
, вращение видно происходящим против хода часовой стрелки. Вдоль стороны 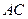 движется точка
движется точка  , имея относительно пластины известную скорость
, имея относительно пластины известную скорость 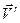 (Рис. 3.3). Определить модуль и направление ускорения Кориолиса.
(Рис. 3.3). Определить модуль и направление ускорения Кориолиса.
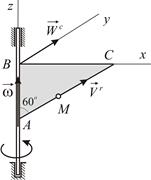 |
| Рис. 3.3 |
В тех случаях, когда ось вращения тела расположена в плоскости рисунка, следует изобразить вектор угловой скорости тела (Рис. 3.3). Ускорение Кориолиса определяем по формуле (7.13):
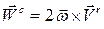 .
.
В данном примере вектор 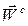 направлен по оси
направлен по оси 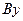 в положительную сторону – так, чтобы, смотря ему навстречу, видеть кратчайший поворот от первого сомножителя
в положительную сторону – так, чтобы, смотря ему навстречу, видеть кратчайший поворот от первого сомножителя 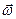 ко второму
ко второму 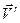 против хода часовой стрелки. Модуль ускорения Кориолиса равен
против хода часовой стрелки. Модуль ускорения Кориолиса равен
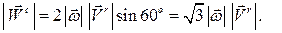
Пример 3.2
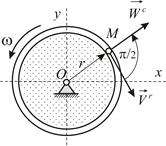 |
| Рис.3.4 |
Круглая пластина вращается вокруг оси 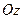 , перпендикулярной плоскости пластины, с угловой скоростью
, перпендикулярной плоскости пластины, с угловой скоростью 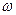 , По ободу пластины движется точка
, По ободу пластины движется точка  , имея относительно пластины известную скорость
, имея относительно пластины известную скорость 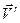 (Рис.3.4). Определить модуль и направление ускорения Кориолиса.
(Рис.3.4). Определить модуль и направление ускорения Кориолиса.
Ось вращения перпендикулярна плоскости чертежа. В таком случае нецелесообразно изображать вектор угловой скорости тела. Укажем круглой стрелкой направление вращения (Рис.3.4). Для определения направления ускорения Кориолиса используем правило Жуковского: повернём вектор относительной скорости в направлении вращения пластины на угол 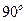 . Угол между вектором угловой скорости тела и относительной скоростью точки в данном случае прямой:
. Угол между вектором угловой скорости тела и относительной скоростью точки в данном случае прямой: