Деформация горных пород в результате механического взаимодействия горных пород и насыщающих их жидкостей

Использование описанных выше общих соотношений механического взаимодействия горных пород и фильтрующихся в них жидкостей покажем применительно к деформации пород вблизи скважин или стволов шахт, а также при изучении влияния деформации пород на процесс фильтрации жидкости в условиях неупругих режимов пластов.

Выше была рассмотрена деформация непроницаемых горных пород вблизи скважин, когда давление жидкости приложено к поверхности скважины. При деформации пористых и проницаемых пород в процессе фильтрации содержащихся в них жидкостей или газов на каждый элементарный объем пористой среды действует соответствующая компонента градиента давления жидкости или газа.

Будем также учитывать наличие обсадной стальной трубы (колонны) в скважине. Внешняя поверхность трубы (рисунок 7.7, а) скреплена с породами пласта при помощи цемента. В целях упрощения задачи будем считать свойства цемента и свойства пород одинаковыми. Примем также, что жидкость не оказывает давления на обсадную трубу, поскольку она перфорирована и, следовательно, очень хорошо проницаема. Деформацию обсадной трубы будем считать упругой. Очевидно, что в рассматриваемом случае каждому значению нормального напряжения в горных породах 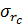, действующего на трубу, будет отвечать определенное значение смещения горных пород вблизи трубы.

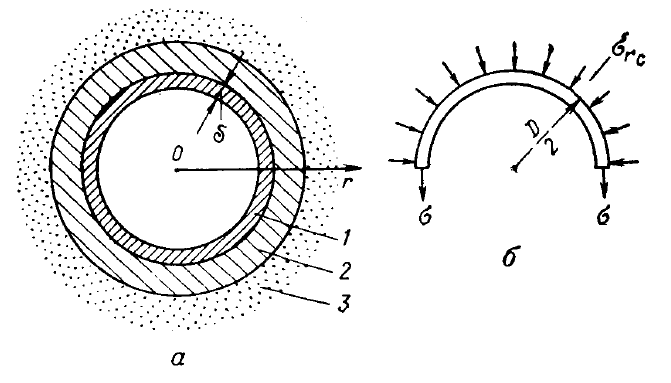
Рисунок 7.7 – Действие градиентов давления на породы пласта

вокруг ствола обсаженной скважины:

1 — обсадная труба; 2 — цементное кольцо; 3 — породы пласта

В соответствии с рисунком 7.7, б получаем следующее соотношение между напряжениями в трубе и в породах при :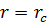

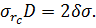(7.5)

Увеличение диаметра 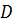определяется следующим образом:

.

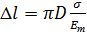(7.6)

где 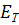— модуль Юнга материала трубы.

Учитывая, что 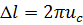, получаем

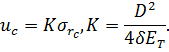		(7.7)

Упругая деформация

Для той части задачи, которая касается фильтрации, примем следующую схему: в области 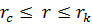существует установившееся движение жидкости, а при 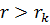жидкость находится в покое. Такая схема с определенным приближением может соответствовать, например, случаям закачки в пласт жидкости с вязкостью, намного превышающей вязкость пластовой жидкости, или при приближенном рассмотрении неустановившейся фильтрации при упругом режиме. Следовательно, для распределения давления жидкости в пласте имеем формулу:

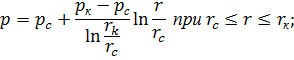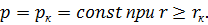(7.8)

Считая деформацию пласта плоской, имеем уравнение равновесия

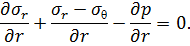(7.9)

И уравнение смещений

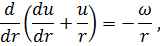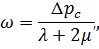(7.10)

где 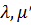- коэффициенты Лямэ.

Уравнение (7.10) имеет решение

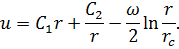(7.11)

Для нормального напряжения, действующего на контакте цемента и обсадной трубой, имеем следующую формулу:

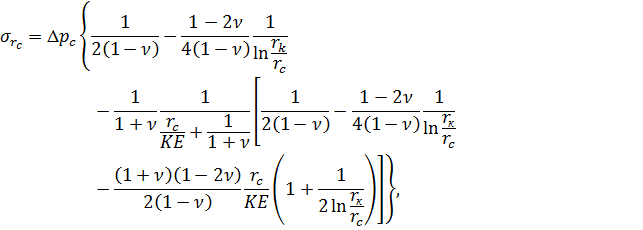(7.12)

где 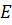– модуль Юнга пород.

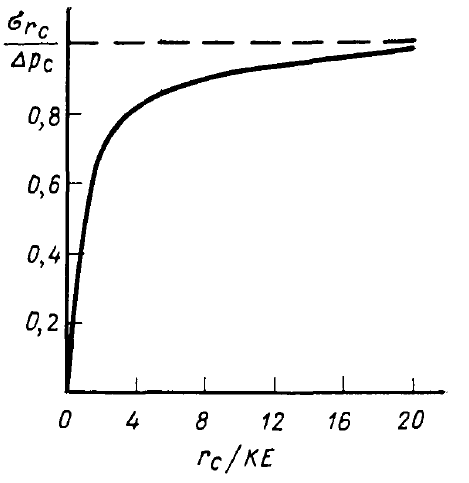
Рисунок 7.8 – Зависимость 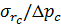от .

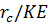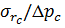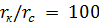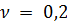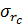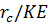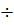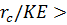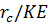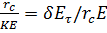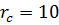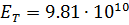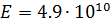На рисунке 7.8 показана зависимость при и , из которой видно, что особенно сильно на влияет величина в пределах ее изменения от 0 до 3 4, а при 20 величина мало влияет на нормальное напряжение, действующее на обсадную трубу. Поскольку , то при см, , Па, 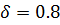см величина 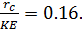при 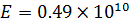Па и тех же остальных условиях 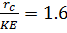. В первом случае, при 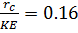, труба оказывает малое влияние на деформацию пласта и можно считать пласт как бы необсаженным. Во втором случае, т. е. при 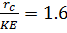, что соответствует примерно условиям, когда пласт сложен мягкими породами (алевролитами, глинами и т. д.), уже нельзя не учитывать наличия обсадной трубы в скважине при рассмотрении деформации горных пород.

Характер деформации системы обсадная труба — пласт влияет также на величину 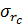. Если 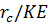достаточно мало, т. е., например, породы обладают большим модулем упругости, то при закачке жидкости в пласт обсадная труба будет деформироваться примерно в той же степени, что и породы пласта, и напряжение 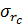отрывающее трубу от цемента, будет сравнительно невелико. Наоборот, если породы имеют меньший модуль упругости, отрывающее напряжение 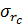может достичь значительной величины.

Пластическая деформация

Представляет интерес описание пластической деформации горных пород под действием градиентов давления фильтрующейся жидкости. Известно, что при строительстве шахт, проходке и эксплуатации нефтяных и газовых скважин создание определенных градиентов давления жидкости в каком-либо пласте, сложенном глинистыми или плохо сцементированными песчаными породами, приводит к тому, что породы разрушаются, «плывут».

Напряжения, возникающие при пластической деформации пород, описываются тем же уравнением (7.9), что и при упругой деформации.

Принимая (как и при изучении пластической деформации непроницаемых пород) гипотезу пластичности 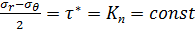, а также установившееся распределение давления вида (7.8), но соответствующее случаю движения жидкости от «контура питания» 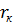к скважине радиусом 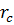, и используя граничное условие 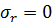при 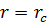, получаем следующее решение задачи:

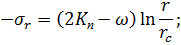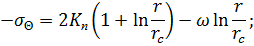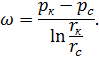(7.13)

Радиус разгрузки 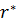в этом случае определяется следующей формулой:

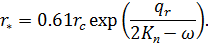(7.14)

Как видно из (7.13) и (7.14), наличие градиентов давления жидкости в пласте при фильтрации из пласта в скважину как бы уменьшает коэффициент пластичности 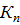и способствует большему распространению пластической деформации неустойчивых пород вблизи скважин.