ПРИМЕНЕНИЕ MathCAD ДЛЯ РЕШЕНИЯ ИНЖЕНЕРНО-СТРОИТЕЛЬНЫХ ЗАДАЧ.

ПРИМЕНЕНИЕ MathCAD ДЛЯ РЕШЕНИЯ ИНЖЕНЕРНО-СТРОИТЕЛЬНЫХ ЗАДАЧ.

Выполнила: студент гр. С-11-08

Дмитриев Дмитрий

Проверил: доцент Козлов А.И.

Чебоксары 2009

Содержание и объем курсовой работы

В соответствии с вариантом задания необходимо решить задачи 3.1-3.8. Пояснительная записка должна иметь обложку из твердой бумаги и должна включать:

титульный лист;

задание;

краткое описание известных методов решения задач;

тексты разработанных документов MathCAD (дополнительно в электронном виде);

результаты решений индивидуального варианта задания с выводами.

Основные приемы работы в системе MathCAD

Одной из основных областей применения ПК являются математи­ческие и научно-технические расчеты. Сложные вычислительные задачи, возникающие при моделировании технических устройств и процессов, можно разбить на ряд элементарных: вычисление интегралов, решение уравнений, решение дифференциальных уравнений и т. д. Для таких за­дач уже разработаны методы решения, созданы математические системы, доступные для изучения студентам младших курсов вузов.

Цель курсовой работы - научить пользоваться простейшими методами вы­числений с использованием современных информационных технологий. Наиболее подходящей для этой цели является одна из самых мощных и эффективных математических систем - MathCAD, которая занимает осо­бое место среди множества таких систем (Matlab, Maple, Mathematica и др.).

MathCAD – это мощная и в то же время простая универсальная среда для решения задач в различных отраслях науки и техники, финан­сов и экономики, физики и астрономии, математики и статистики, строительной механики и т.д. MathCAD остается единственной системой, в которой описание решения математических задач задается с помощью привычных математических формул и знаков. MathCAD позволяет выполнять как численные, так и аналитические (символьные) вычисления, имеет чрезвычайно удобный математико-ориентированный интерфейс и прекрасные средства научной графики. MathCAD работает с документами. С точки зрения пользователя, документ - это чистый лист бумаги, на котором можно размещать блоки трех основных типов: математические выражения, текстовые фрагменты и графические области.

Расположение нетекстовых блоков в документе имеет принципи­альное значение – слева направо и сверху вниз.

Математические выражения

К основным элементам математических выражений MathCAD от­носятся типы данных, операторы, функции и управляющие структуры.

Операторы

Операторы - элементы MathCAD, с помощью которых можно создавать математические выражения. К ним, например, относятся сим­волы арифметических операций, знаки вычисления сумм, произведений, производной и интеграла и т.д.

Оператор определяет:

1. действие, которое должно выполняться при наличии тех или иных значений операндов;

2. сколько, где и какие операнды должны быть введены в оператор.

Операнд – число или выражение, на которое действует оператор. Например, в выражении 5! + 3число 3и выражение 5! –операнды опера­тора +(плюс), а число 5операнд оператора факториал (!). После указания операндов операторы становятся исполняемыми по документу блоками.

Типы данных

К типам данных относятся числовые константы, обычные и сис­темные переменные, массивы (векторы и матрицы) и данные файлового типа.

Константами называют поименованные объекты, хранящие не­которые значения, которые не могут быть изменены. Переменные явля­ются поименованными объектами, имеющими некоторое значение, кото­рое может изменяться по ходу выполнения программы. Тип переменной определяется ее значением; переменные могут быть числовыми, строко­выми, символьными и т. д. Имена констант, переменных и иных объектов в MathCAD представ­ляют собой набор латинских или греческих букв и цифр. В MathCAD содержится небольшая группа особых объектов, кото­рые нельзя отнести ни к классу констант, ни к классу переменных, значе­ния которых определены сразу после запуска программы. Их правильнее считать системными переменными, имеющими предопределенные сис­темой начальные значения (Приложение 1). Изменение значений сис­темных переменных производят во вкладке Встроенные переменныедиалогового окна Math Optionsкоманды МатематикаÞ Опции.

Обычные переменные отличаются от системных тем, что они должны быть предварительно определены пользователем, т. е. им необ­ходимо хотя бы однажды присвоить значение. В качестве оператора присваивания используется знак :=,тогда как знак = отведен для вывода значения константы или переменной.

Если переменной присваивается начальное значение с помощью оператора := (вызывается нажатием клавиши : (двоеточие) на клавиатуре), то такое присваивание называется локальным. До этого присваивания пере­менная не определена и ее нельзя использовать. Однако с помощью знака { (клавиша ~на клавиатуре) можно обеспечить глобальное присваивание. MathCAD прочитывает весь документ дважды слева направо и сверху вниз. При первом проходе выполняются все дей­ствия, предписанные глобальным оператором присваивания ({), а при вто­ром – производятся действия, предписанные локальным оператором присваивания (:=),и отображаются все необходимые результаты вычис­лений (=).

Существуют также жирный знак равенства =(комбинация клавиш Ctrl +=), который используется, например, как оператор приближенного равенства при решении систем уравнений, и символьный знак равенства (комбинация клавиш Ctrl + .).

Дискретные аргументы - особый класс ранжированных переменных, который в пакете MathCAD зачастую заменяет управляющие структуры, называе­мые циклами (однако полноценной такая замена не является). Эти пере­менные имеют ряд фиксированных значений, либо целочисленных (1 способ), либо в виде чисел с определенным шагом, меняющихся от на­чального значения до конечного (2 способ).

1. Name := Nbegin .. Nend,

где Name – имя переменной, Nbegin – ее начальное значение, Nend – ко­нечное значение, .. – символ, указывающий на изменение переменной в заданных пределах (вводится клавишей ;). Если Nbegin < Nend, то шаг переменной будет равен +1, иначе –1.

2. Name := Nbegin, (Nbegin + Step) .. Nend

Здесь Step – заданный шаг изменения переменной (он должен быть по­ложительным, если Nbegin < Nend, или отрицательным в обратном слу­чае).

Дискретные аргументы значительно расширяют возможности MathCAD, позволяя выполнять многократные вычисления или циклы с повторяющимися вычислениями, формировать векторы и матрицы.

Массив - имеющая уникальное имя совокупность конечного числа числовых или символьных элементов, упорядоченных некоторым обра­зом и имеющих определенные адреса. В пакете MathCAD используются массивы двух наиболее распространенных типов:

· одномерные (векторы);

· двумерные (матрицы).

Порядковый номер элемента, который является его адресом, назы­вается индексом. Индексы могут иметь только целочислен гументами и парамет­рами функции. Переменные, указанные в скобках после имени функции, являются ее аргументами и заменяются при вычислении функции значе­ниями из скобок. Переменные в правой части определения функции, не указанные скобках в левой части, являются параметрами и должны за­даваться до определения функции.

Главным признаком функции является возврат значения, т.е. функция в ответ на обращение к ней по имени с указанием ее аргументов должна возвратить свое значение.

Функции в пакете MathCAD могут быть встроенные, т. е. заблаговременно введенные разработчиками, или определен­ные пользователем.

Способы вставки встроенной функции:

1.Выбрать пункт меню ВставкаÞ Функция.

2.Нажать комбинацию клавиш Ctrl + E.

Текстовые фрагменты представляют собой куски текста, которые пользователь хотел бы видеть в своем документе. Существуют два вида текстовых фрагментов:

· текстовая область предназначена для небольших кусков текста - подписей, комментариев и т. п. Вставляется с помощью команды ВставкаÞ Текстовая регионили комбинации клавиш Shift + "(двойная кавычка);

• текстовый абзац применяется в том случае, если необходимо ра­ботать с абзацами или страницами. Вставляется с помощью ком­бинации клавиш Shift + Enter.

Графические области

Графические области делятся на три основных типа - двумерные графики, трехмерные графики и импортированные графические образы. Двумерные и трехмерные графики строятся самим MathCAD на основа­нии обработанных данных.

Для создания декартового графика:

1. Установить визир в пустом месте рабочего документа.

2. Выбрать команду ВставкаÞ ГрафикÞ Х-У график,или нажать комбинацию клавиш Shift + 2,или щелкнуть кнопку Графики.Появится шаблон панели декартового графика.

3. Ввести в средней метке под осью Х первую независимую пере­менную, через запятую – вторую и так до 10, например х1, х2, …

4. Ввести в средней метке слева от вертикальной оси Y первую независимую переменную, через запятую – вторую и т. д., например у1(х1), у2(х2), …, или соответствующие выражения.

5. Щелкнуть за пределами области графика, чтобы начать его по­строение.

Табулирование функций

Данная задача часто встречается в инженерной практике. Обычно функции, описывающие какой-либо процесс, весьма громоздки и создание таблиц их значений требует большого объема вычислений.

Рассмотрим два случая табулирования функции:

1. с постоянным шагом изменения аргументов;

2. с произвольным набором значений аргумента.

Пример: Вычислить при 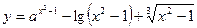a = 2.25;

х_i изменяется с шагом Dх = 0.5; х_п = 1.2; х_к = 3.7.

Текст документа MathCAD :

Пример: Вычислить и вывести на экран значения функции 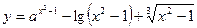при х₁ = 1.28 х₂ = 1.36 х₃ = 2.47 х₄ = 3.68 х₅ = 4.6; а =1.6

Цикл организуется для одномерного массива.

Текст документа MathCAD :

Вывод:Я научился табулировать функции с постоянным и переменным шагом также вычислять и выводить на экран значения функции.

Аппроксимация функций

Одним из распространенных и практически важных случаев связи между аргументом и функцией является задание этой связи в виде некоторой таблицы {x_i ; y_i}, например, экспериментальные данные. На практике часто приходится использовать табличные данные для приближенного вычисления у при любом значении аргумента х (из некоторой области). Этой цели служит задача о приближении (аппроксимации) функций: данную функцию f(x) требуется приближенно заменить некоторой функцией g(х) так, чтобы отклонение g(х) от f(x) в заданной области было наименьшим. Функция g(х) при этом называется аппроксимирующей. Если приближение строится на заданном дискретном множестве точек {x_i}, то аппроксимация называется точечной. К ней относятся интерполирование, среднеквадратичное приближение и др.

Пример: Используя линейную аппроксимацию и гиперболическую получить эмпирическую формулу для функции у=f(x), заданной в табличном виде:

12.	xi	-25.0	-23.0	-21.0	-18.0	-17.2	-15.4	-14.0
yi	0.76	0.74	0.61	0.58	0.84	0.92	1.28

Текст документа MathCAD.

Линейная аппроксимация

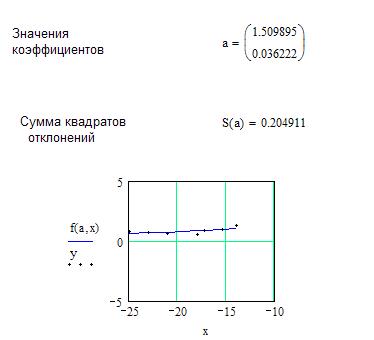
Сумма квадратов отклонений указывает на статистическую оценку среднеквадратической погрешности. Чем она меньше, тем точнее полученная аппроксимирующая функция у = g(х). Для зависимости в виде полинома второй степени необходимо изменить выражение для аппроксимирующей зависимости и добавить начальное приближение для коэффициента a₂.

Вывод: Я научился, используя линейную аппроксимацию получать эмпирическую формулу для функции.

Уравнений.

Многие задачи физики, химии, экологии, строительной механики и других разделов науки и техники при их математическом моделировании сводятся к дифференциальным уравнениям. Поэтому решение дифференциальных уравнений является одной из важнейших математических задач.

Среди множества численных методов решения дифференциальных уравнений наиболее простые – это явные одношаговые методы. К ним относятся методы Рунге-Кутта различных порядков.

Требуется найти функцию у = у(х), удовлетворяющую уравнению

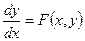(3.3)

и принимающую при х = х₀ заданное значение у₀:

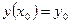. (3.4)

При этом решение необходимо получить в интервале х₀ £ х £ х_к. Из теории дифференциальных уравнений известно, что решение у(х) задачи Коши (3.3), (3.4) существует, единственно и является гладкой функцией, если правая часть F(x, y) удовлетворяет некоторым условиям гладкости. Численное решение задачи Коши методом Рунге-Кутта 4-го порядка заключается в следующем. На заданном интервале [х₀, х_к] выбираются узловые точки. Значение решения в нулевой точке известно у(х₀) = у₀. В следующей точке у(х₁) определяется по формуле

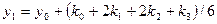, (3.5)

здесь

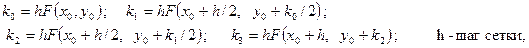(3.6)

т. е. данный вариант метода Рунге-Кутта требует на каждом шаге четырехкратного вычисления правой части уравнения (3.3). Mathcad располагает обширным набором функций, позволяющих успешно решать обыкновенные дифференциальные уравнения и их системы.

Пример: Построить графики и вывести в виде таблицы приближенное решение задачи Коши на отрезке [0; 1] с помощью функции Odesolve при количестве шагов N=5 и N=20. Сравнить результаты в одинаковых точках. Оценить влияние количества шагов на точность решения. 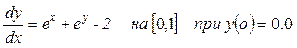. (3.7)

Текст документа MathCAD.

N=10

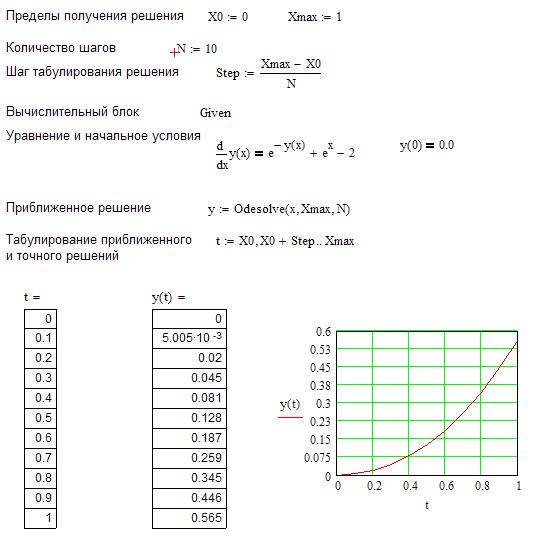
N=20

Вывод:Я научиля численному решение обыкновенных дифференциальных уравнений и выявил что при увеличении шагов график функции становится более гладким и зачения в одинаковых точках совпадают.

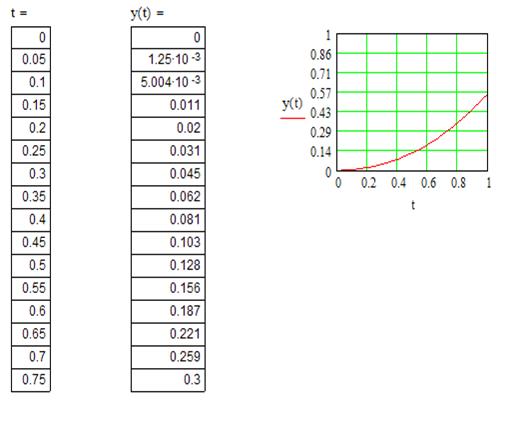
Текст документа MathCAD

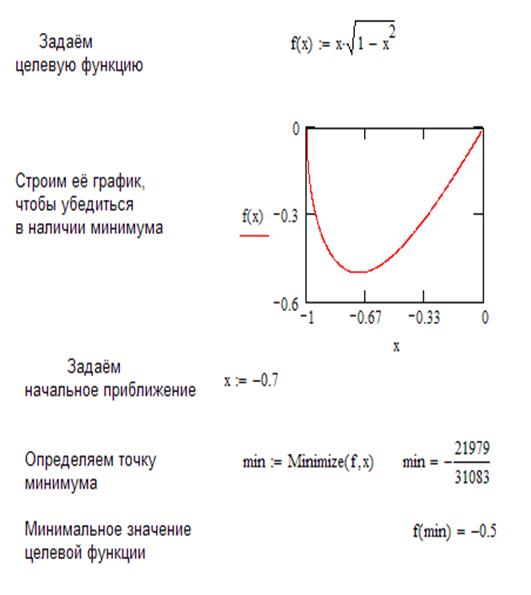
Пример. Найти и вывести на печать координаты и минимальное значение функции двух переменных при погрешностях 10^-2, 10^-20 функции двух переменных f(x, y) = 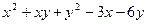, если начальная точка поиска имеет координаты М₀ (0.5; .5).

Текст документа MathCAD

погрешность= 10^-2

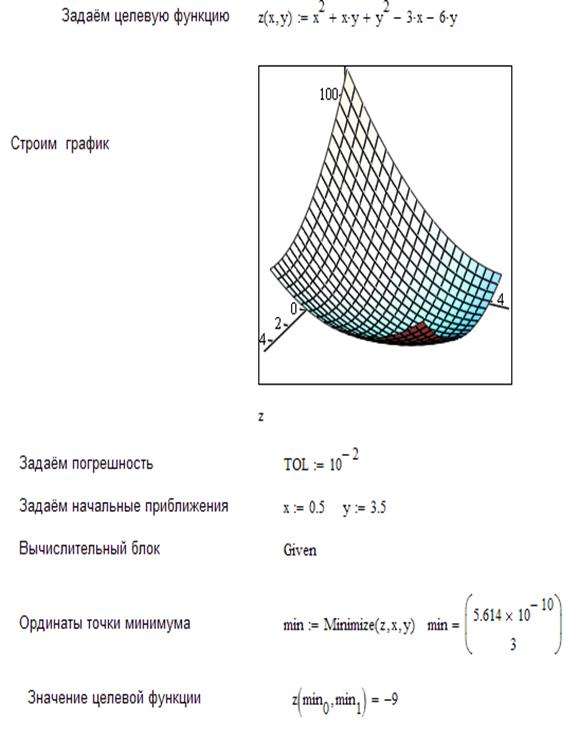
погрешность= 10^-20

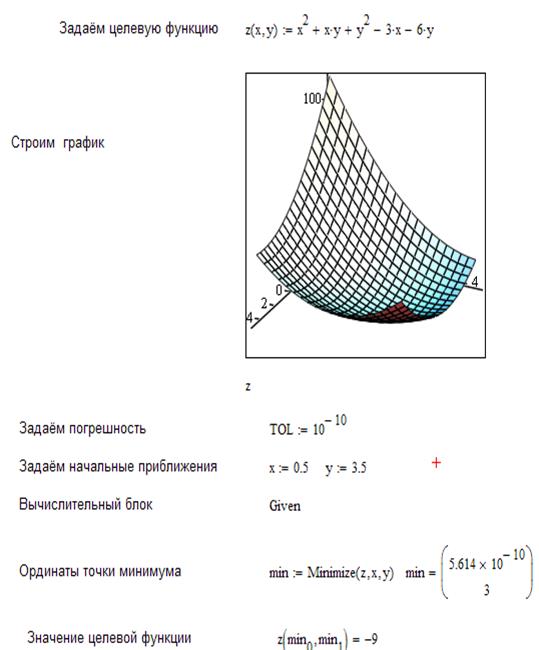
Вывод:Я научился решать оптимизационные задачи 2-х типов: безусловные и условные

Общий вывод:Янаучился пользоваться простейшими методами вы­числений в математической системе MathCAD, которая является одной из самых мощных и эффективных математических систем.В процессе выполнения работы я заметил, что MathCAD остается единственной системой, в которой описание решия математических задач задается с помощью привычных математических формул и знаков. MathCAD позволяет выполнять как численные, так и аналитические (символьные) вычисления, имеет чрезвычайно удобный математико-ориентированный интерфейс и прекрасные средства научной графики.

Литература

1. Mathcad 6.0 Plus. Финансовые, инженерные и научные расчеты в сре­де Windows 95./Перевод с англ. - М.: Информационно-издательский дом “Филинъ”, 1996. -712 с.

2. Дьяконов В.П. Справочник по MathCAD PLUS 6.0 PRO. - М.: “СК Пресс”, 1997. - 336 с.: ил.

3. Дьяконов В.П., Абраменкова И.В. MathCAD 8 PRO в математике, фи­зике и Internet. - М.: “Нолидж”, 2000. - 512 с.: ил.

4. Кудрявцев Е.М. MathCAD 2000 Pro. – М.: ДМК Пресс, 2001. – 576 с.: ил.

5. Очков В. Ф. Mathcad 7 Pro для студентов и инженеров. - М.: Компью­терПресс, 1998. - 384 с.: ил.

6. Плис А.И., Сливина Н.А. Mathcad 2000. Лабораторный практикум по высшей математике. - М.: Высш. шк., 2000. - 716 с.: ил.

ПРИМЕНЕНИЕ MathCAD ДЛЯ РЕШЕНИЯ ИНЖЕНЕРНО-СТРОИТЕЛЬНЫХ ЗАДАЧ.

Выполнила: студент гр. С-11-08

Дмитриев Дмитрий