Приближенные методы решения обыкновенных дифференциальных уравнений. Метод конечных разностей.
Задание:
1) Используя метод конечных разностей, составить решение краевой задачи для обыкновенного дифференциального уравнения с точностью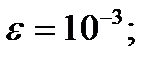 
шаг h=0,1.
Теоретическая часть.
Исчисление конечных разностей связано с изучением свойств и применений разностей между соседними членами какой-нибудь последовательности или между значениями функции в точках, расположенных с постоянным интервалом в некотором пространстве. Слово «конечные» используется здесь в несколько устаревшем смысле «не бесконечно малые», т.е. не связанные с предельными переходами. Поскольку дифференциальное исчисление занимается изучением пределов разностей, а исчисление конечных разностей – самими разностями, то естественно, что между этими двумя теориями существует много параллелей. Исчисления конечных разностей используются при интерполяции в математических таблицах, при суммировании числовых рядов, при вычислении интегралов и дифференцировании функций. Разности встречаются также в любой ситуации, когда надо описать поведение объекта, который испытывает воздействие меняющихся условий на определенном расстоянии (во времени и в пространстве). Например, термостату требуется значительное время, чтобы отреагировать на изменение температуры, поэтому он реагирует не на текущую температуру, а на ту, что была минуту назад. Другой пример: автомашиной управляет водитель, которому требуется какое-то время, чтобы отреагировать на возникшую на дороге ситуацию.
Под конечной разностью первого порядка функции f (x) принято понимать величину
(1) 
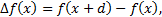
где d – некоторая постоянная, которую часто, но не всегда, принимают равной 1. Разность второго порядка обозначается D2f и представляет собой разность разностей, т.е.
(2) 
.
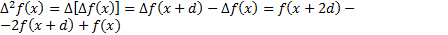Продолжив этот процесс, мы получим разности более высоких порядков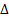 
3f (x), 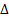4f (x), ј .
Данные выше определения можно также применить к членам любых последовательностей величин, например, к последовательности 3, 6, 11, 18, 27, 38, ј.
Первые разности равны:
6 – 3, 11 – 6, 18 – 11, 27 – 18, 38 – 27, ј, т.е. 3, 5, 7, 9, 11, ј;
Разности второго порядка постоянны и равны 2.
В общем виде такие последовательности можно записать как
(3) 
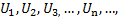
где разности первого, второго и т.д. порядков определяются выражениями
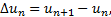
(4) 
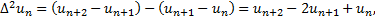
а n может принимать любое допустимое для индекса значение.
В некоторых приложениях используются последовательности вида
(5) 
, 
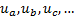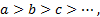
где индексы могут принимать любые убывающие значения. В этом случае вместо символа D используется символ «разделенной разности». Разделенные разности первого и второго порядков определяются следующим образом:
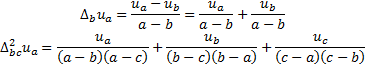
Помимо уже названных выше приложений, исчисление конечных разностей используется в страховании, теории вероятностей и статистике. В последние годы с изобретением быстродействующих компьютеров конечные разности стали все более широко применяться при решении дифференциальных уравнений, обыкновенных и в частных производных, многие из которых ранее было невозможно решить другими математическими методами.
Варианты заданий
№ 1. № 2
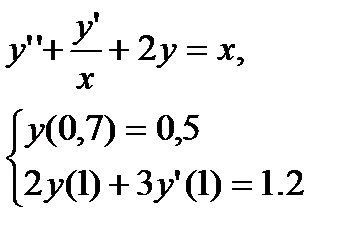
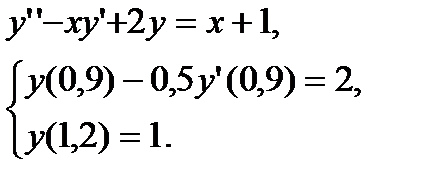
№ 3 № 4
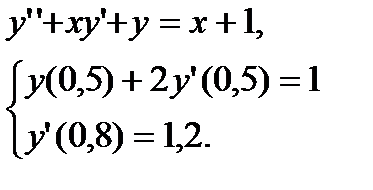
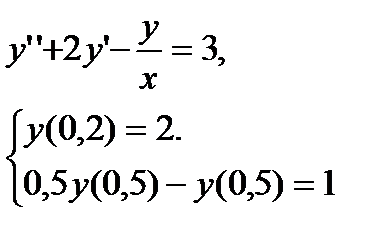
№ 5 № 6
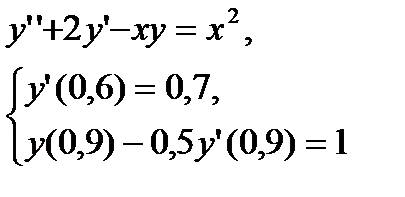
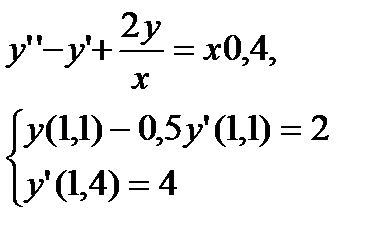
№ 7 № 8
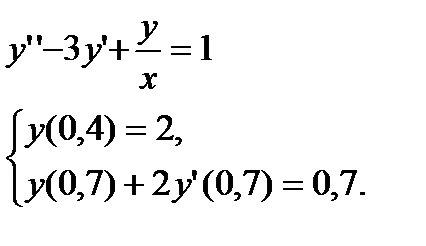
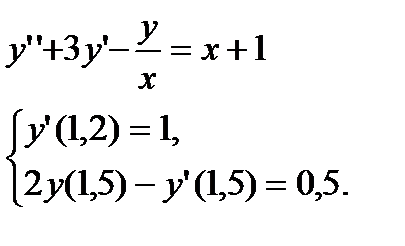
№ 9 № 10
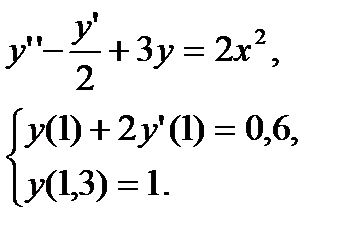
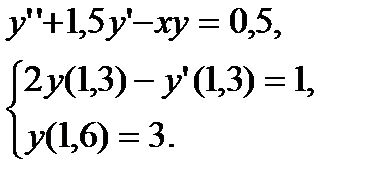
№ 11 № 12
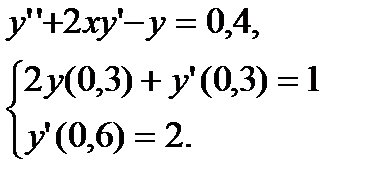
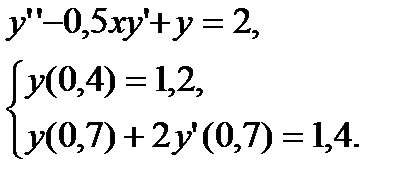
№ 13 № 14
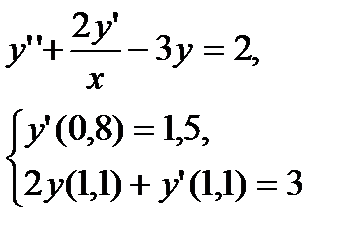
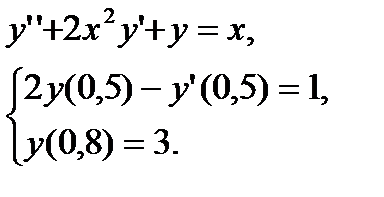
№ 15 № 16
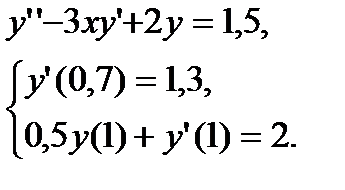
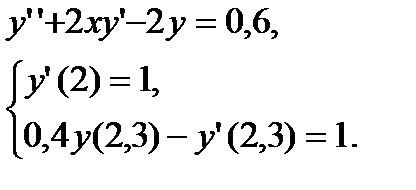
№ 17 № 18
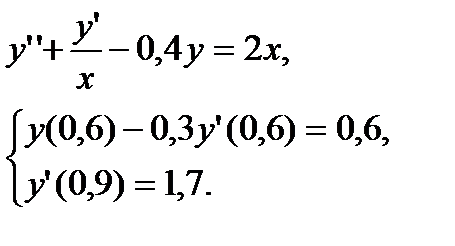
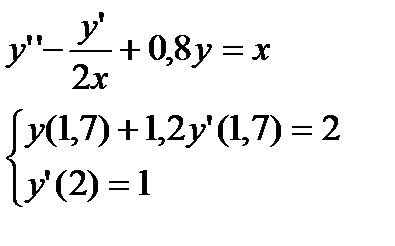
№ 19 № 20
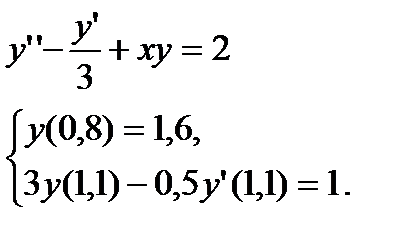
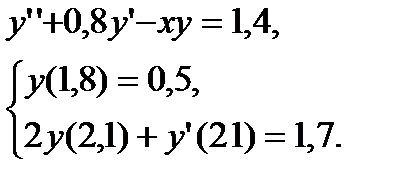
№ 21 № 22
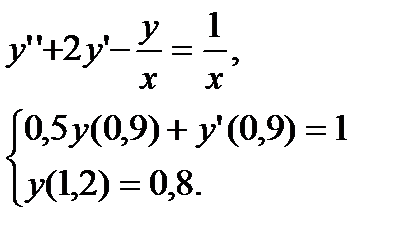
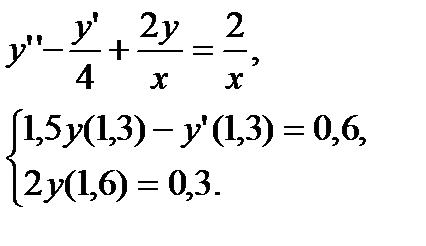
№ 23 № 24
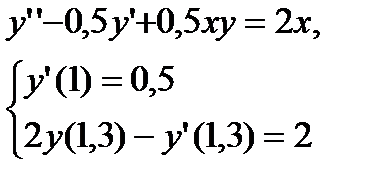
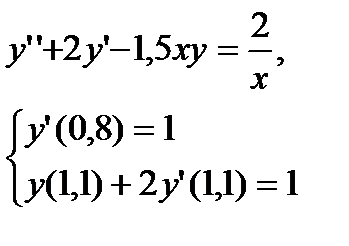
№ 25 № 26
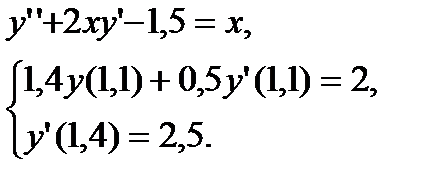
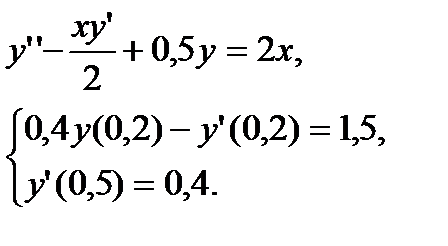
№ 27 № 28
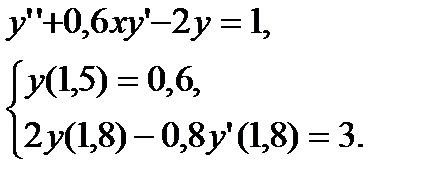
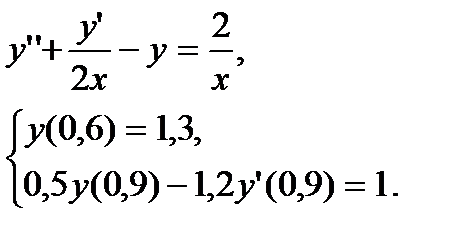
№ 29 № 30
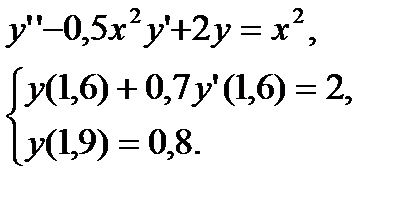
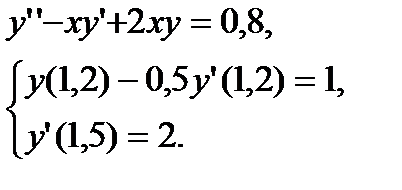
Образец выполнения задания
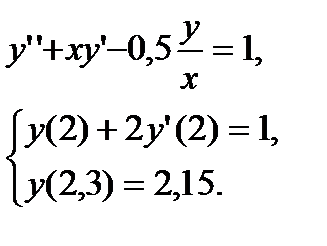
Разбив отрезок [2; 2,3] на части с шагом h=0,1 (рис. 7) получим четыре узловые точки с абсциссами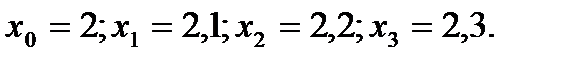 
Две точк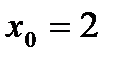и 
и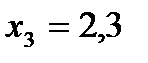 
являются конечными, а две другие –
2,0 2,1 2,2 2,3
Рис. 7
Внутренними. Данное уравнение во внутренних точках заменим конечно-разностным уравнением
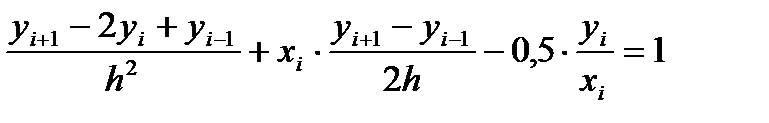(i=1, 2).
Из краевых условий составим конечно-разностные уравнения в конечных точках:
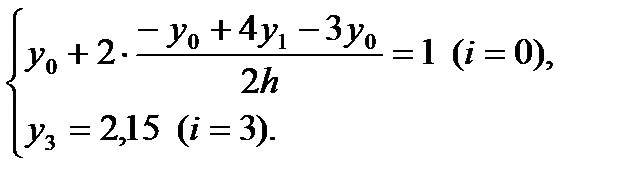
Данная задача сводиться к решению системы уравнений
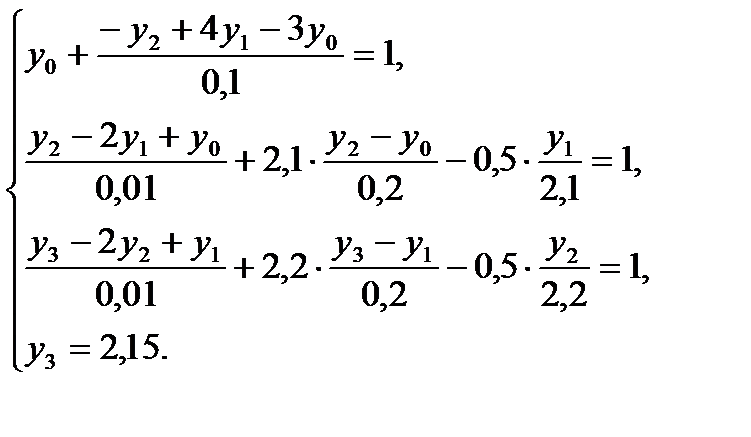
Выполнив преобразование имеем
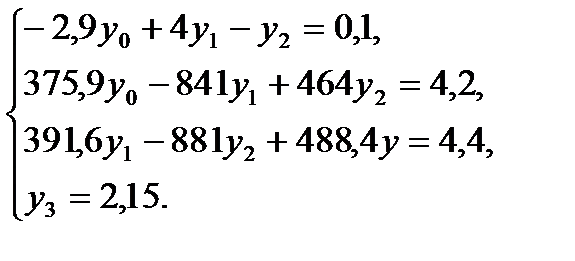
Подставив значение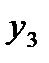 
в третье уравнение, получим для определения остальных неизвестных систему
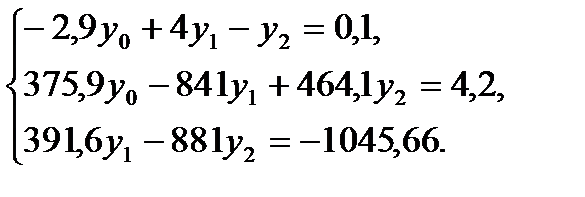
Для решения полученной системы воспользуемся, например, схемой «главных элементов».
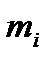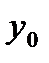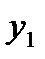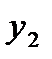 |  |  |  | Свободные члены |  | |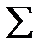
| -0,00113507 0,526788 -1 | -2,9 375,9 | -841 391,6 | -1 464,1
| 0,1 4,2 -1045,66 | 0,2 3,2 -1535,06 | |
| 0,00560179 -1 | -2,9 375,9 | 3,55551
| - - | 1,28690 -546,6411 | 1,94240 -805,4511 | |
| -1 | -79429 | - | - | -1,77527 | -2,56957 | |
| 2,2350 3,2351 | 2,1849 3,1849 | 2,1580 3,1580 |
Ответ:
| x | y | x | Y |
| 2,0 | 2,235 | 2,2 | 2,158 |
| 2,1 | 2,185 | 2,3 | 2,150 |
Контрольные вопросы
1) Объяснить метод конечных разностей.
2) Дать определение разности схем.
3) Описать сущность метода сеток.
4) Дать определение узла и сетки.
5) Суть прямого и обратного хода метода прогонки.
6) Алгоритм метода конечных разностей.
Заключение
Методических указаний составлены для повышение уровня самостоятельной работы студентов при выполнении лабораторных работ по курсу « Моделирование систем».
Методические указания составлены в соответствии с программой курса «Моделирование систем». В них содержится информация по пяти лабораторным работам:
· Методы решения систем линейных уравнений
· Методы решения систем нелинейных уравнений.
· Численное дифференцирование и интегрирование в математическом моделировании, вычисление интегралов методом прямоугольников.
· Численное дифференцирование и интегрирование в математическом моделировании, вычисление интегралов методом Симпсона и методом трапеций
· Приближенные методы решения обыкновенных дифференциальных уравнений методом конечных разностей
В каждой лабораторной работе содержатся теоретическая часть, цель работы, порядок выполнения работы, отчетность, вопросы по зачетам и список литературы.
К выполнению лабораторных работ студенты могут приступить только после изучения соответствующего раздела курса, используя настоящее пособие и техническую литературу, приведенную в конце методических указаний.
Разрешение на выполнение работ дает преподаватель, после того, как убедится в наличии у студентов знаний по выполнению и оформлению соответствующей работы.
В каждом отчете по лабораторной работе должны быть сделаны выводы по результатам работы.
Защита лабораторных работ производится индивидуально по теоретическому и практическому материалу. В случае несоответствия результатов расчетов с правильным решением студенты в ходе зачета должны дать соответствующие пояснения.
Настоящие методические указания помогут студентам подготовиться к лабораторным занятиям, повышать качество отчета и ее защиту.
Список литературы
1. Воробьева Г.Н. Данилова А.Н."Практикум по вычислительной математике"М.:"Высшая школа" 1990.
2. Демирчан К.С., Бутырин П.А."Моделирование и машинный расчет электрических цепей."-М.:"Высшая школа"1998.
3."Моделирование и оптимизация на ЭВМ радиоэлектронных устройств."/ под ред. Бенсона Э.М.: М."Радио и связь"1981.
моделирование систем управления
Методические указания для студентов направления: 220400.62 «Управление и информатика в технических системах».
Составители: Глухов Дмитрий Олегович, Петухов Игорь Валерьевич.
Редактор: Чернышев А. Ю, к.т.н., доцент
ПЛД № 2018 от
Подписано в печать 15.10.03 Формат 60´84/16. Бумага офсетная.
Печать офсетная. Усл.печ.л. Уч.-изд.л. 2,1
Тираж 200 экз. Заказ № .С-130
Поволжский государственный технологический университет 424000 Йошкар-Ола, пл. Ленина, 3
Отдел оперативной полиграфии
Поволжский государственный технологический университет 424006 Йошкар-Ола, ул. Панфилова, 17