Построение графиков функций в полярной системе координат
В простейших случаях допустимо строить график функции, заданной в полярных координатах, по точкам (см. пример занятия 15).
Построение графика функции ρ=f( 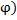 в общем случае осуществляется так: а) строят для функции ρ=f(
в общем случае осуществляется так: а) строят для функции ρ=f( 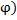 соответствующую функцию y=f(x); б) исследуют функцию ρ=f(
соответствующую функцию y=f(x); б) исследуют функцию ρ=f( 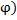 , сравнивая ее с соответствующей функцией y=f(x), учитывая отмеченные выше особенности графика функции ρ=f(
, сравнивая ее с соответствующей функцией y=f(x), учитывая отмеченные выше особенности графика функции ρ=f( 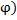 ; в) выполняют построение графика функции ρ=f(
; в) выполняют построение графика функции ρ=f( 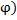 по графику функции y=f(x).
по графику функции y=f(x).
Ограниченность функции.
Если функция y=f(x) ограничена (M<f(x)<N) то, как известно, ее график располагается между прямыми y=M и y = N. Для соответствующей функции ρ=f(  ) справедливо неравенство M<f(
) справедливо неравенство M<f(  )<N, и график функции ρ=f(
)<N, и график функции ρ=f(  ) располагается в кольце, внутренний радиус которого равен М, а внешний –N.
) располагается в кольце, внутренний радиус которого равен М, а внешний –N.
Монотонность функции.
Если функция y=f(x) имеет экстремум при x= 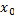 , то функция ρ=f(
, то функция ρ=f( 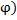 имеет экстремум при
имеет экстремум при  =
= 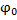 . Если функция y=f(x) убывает в некотором промежутке, то в полярной системе координат для функции ρ=f(
. Если функция y=f(x) убывает в некотором промежутке, то в полярной системе координат для функции ρ=f( 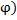 при движении по часовой стрелке значение радиуса уменьшается, а при движении против часовой стрелки – увеличивается.
при движении по часовой стрелке значение радиуса уменьшается, а при движении против часовой стрелки – увеличивается.
Асимптоты функции.
Горизонтальная асимптота y=c кривой y=f(x) в декартовой системе координат переходит в асимптотическую окружность ρ=с в полярной системе координат. В частности, если с=0, то окружность вырождается в точку.
Вертикальная асимптота x=b кривой y=f(x) в декартовой системе координат переходит в общем случае в луч  =b в полярной системе координат. В частности, если b=0, то асимптота х=0 переходит в полярной системе координат в полярную ось; если b=
=b в полярной системе координат. В частности, если b=0, то асимптота х=0 переходит в полярной системе координат в полярную ось; если b= 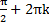 , где k – некоторое целое число, то асимптота x=b переходит в вертикальный луч
, где k – некоторое целое число, то асимптота x=b переходит в вертикальный луч  =
= 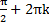 .
.
Замечание. Для построения графика функции ρ=f( 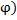 при значениях
при значениях  , соответствующих таким значениям х, при которых f(x) <0, достаточно построить график функции y=│f(x)│. Затем по этому графику строят кривую в полярной системе координат и поворачивают ее вокруг полюса на угол π. Получают кривую, соответствующую отрицательным значениям функции ρ=f(
, соответствующих таким значениям х, при которых f(x) <0, достаточно построить график функции y=│f(x)│. Затем по этому графику строят кривую в полярной системе координат и поворачивают ее вокруг полюса на угол π. Получают кривую, соответствующую отрицательным значениям функции ρ=f( 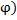 . Следовательно, построение кривой ρ=f(
. Следовательно, построение кривой ρ=f( 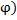 надо вначале выполнить для
надо вначале выполнить для  , соответсвующих значениям х, при которых f(x)>0, а затем строить кривую ρ=f(
, соответсвующих значениям х, при которых f(x)>0, а затем строить кривую ρ=f( 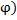 для
для  , соответствующих значениям х, при которых f(x)<0.
, соответствующих значениям х, при которых f(x)<0.
Задания.
Построить график функции в полярной системе координат
- ρ=3sin2
 (четырехлепестковая роза ρ=аsin2
(четырехлепестковая роза ρ=аsin2  )
)
Решение.
Исследуем функцию ρ=3sin2  , сравнивая ее с функцией y=3sin2
, сравнивая ее с функцией y=3sin2 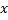 . Функция y=3sin2
. Функция y=3sin2 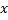 определена для любых х, следовательно, функция ρ=3sin2
определена для любых х, следовательно, функция ρ=3sin2  тоже определена для любых
тоже определена для любых  , Функция y=3sin2
, Функция y=3sin2 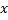 нечетная, следовательно, кривая ρ=3sin2
нечетная, следовательно, кривая ρ=3sin2  симметрична относительно полюса, Поскольку функция y=3sin2
симметрична относительно полюса, Поскольку функция y=3sin2 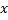 периодическая с периодом π, то и функция ρ=3sin2
периодическая с периодом π, то и функция ρ=3sin2  периодическая в периодом π. Функция y=3sin2
периодическая в периодом π. Функция y=3sin2 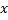 ограничена (│3sin2
ограничена (│3sin2 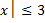 ), следовательно, функция ρ=3sin2
), следовательно, функция ρ=3sin2  тоже ограничена (│3sin2
тоже ограничена (│3sin2  │≤3). Функция y=3sin2
│≤3). Функция y=3sin2 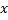 на [0;π] имеет максимум при х=
на [0;π] имеет максимум при х= 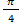 (y=3) и минимум при х=
(y=3) и минимум при х= 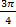 (y=-3). Соответственно, функция ρ=3sin2
(y=-3). Соответственно, функция ρ=3sin2  имеет экстремальные значения при
имеет экстремальные значения при
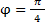
 =
= 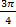 эти значения равны 3 и -3.
эти значения равны 3 и -3.
Функция y=3sin2 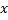 при x
при x 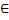 ]0;
]0; 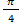 [
[ 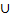 ]
] 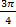 ;
; 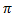 [ возрастающая при x
[ возрастающая при x 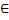 ]
] 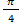 ;
; 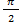 [
[ 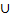 ]
] 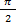 ;
; 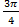 [ убывающая; соответственно, функция, ρ=3sin2
[ убывающая; соответственно, функция, ρ=3sin2  возрастающая при
возрастающая при 
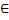 ]
] 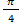 ;
; 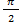 [
[ 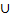 ]
] 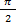 ;
; 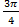 [. Кривая y=3sin2
[. Кривая y=3sin2 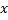 асимптот не имеет, не имеет их и кривая ρ=3sin2
асимптот не имеет, не имеет их и кривая ρ=3sin2  . Следовательно, кривая ρ=3sin2
. Следовательно, кривая ρ=3sin2  располагается в круге радиусом 3 с центром в полюсе.
располагается в круге радиусом 3 с центром в полюсе.
Учитывая симметрию кривой ρ=3sin2  относительно полюса и ее периодичность, строим кривую ρ=3sin2
относительно полюса и ее периодичность, строим кривую ρ=3sin2  для 0≤
для 0≤ 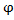 ≤
≤ 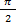 . Это построение выполняем так: сначала строим точку экстремума
. Это построение выполняем так: сначала строим точку экстремума
A1( 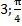 ) и точки, для которых ρ = 0: A2(
) и точки, для которых ρ = 0: A2( 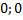 ), A1(
), A1( 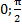 ); после этого строим точки B1(ρ;
); после этого строим точки B1(ρ; 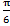 ), B2(ρ;
), B2(ρ; 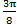 ) .
) .
Заметим, что значения ρ для точек B1 и B2 получим из графика функции y=3sin2 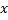 , взяв соответствующую ординату кривой для точек х=
, взяв соответствующую ординату кривой для точек х=  и х=
и х= 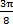 . Аналогично строим точки С1 и С2 . Проведя через эти точки линию, получим график функции ρ=3sin2
. Аналогично строим точки С1 и С2 . Проведя через эти точки линию, получим график функции ρ=3sin2  для 0≤
для 0≤ 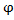 ≤
≤ 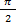 (рис 298, а). Учитывая симметрию относительно полюса, строим кривую ρ=3sin2
(рис 298, а). Учитывая симметрию относительно полюса, строим кривую ρ=3sin2  для -
для - 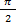 ≤
≤ 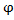 ≤0 (рис 298, б). Наконец, с помощью поворота на угол
≤0 (рис 298, б). Наконец, с помощью поворота на угол 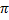 вокруг полюса получаем график функции ρ=3sin2
вокруг полюса получаем график функции ρ=3sin2  (рис 298 в).
(рис 298 в).
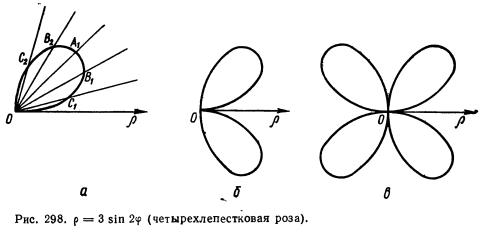
- ρ=αcos2
 (четырехлепестковая роза)
(четырехлепестковая роза)
Решение.
Воспользовавшись формулой cos2  =sin(
=sin( 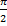 +2
+2  ) приведем заданную функцию к виду
) приведем заданную функцию к виду
ρ =αsin( 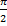 +2
+2  ).
).
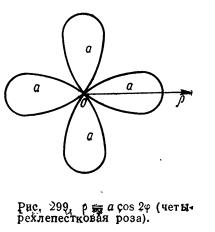 |
Очевидно, что график функции ρ =αsin(
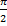 +2
+2  ) получим из графика функции ρ=αcos2
) получим из графика функции ρ=αcos2  с помощью поворота на
с помощью поворота на 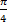 (рис 299)
(рис 299) - ρ=
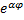 , или ln ρ=α
, или ln ρ=α 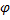 (логарифмическая спираль), α>0
(логарифмическая спираль), α>0 - ρ =
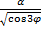 ,
, 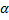 >0.
>0. - ρ =
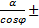 b (конхоида)
b (конхоида)
Занятие 17.
Тема занятия: «Контрольная работа № 2.»
План занятия.
1. Контрольная работа № 2.
Методические материалы.
Содержит задачи из разделов: "Основные тригонометрические функции и обратные тригонометрические функции", "Преобразование тригонометрических выражений", "Показательная функция. Показательные уравнения и неравенства", "Логарифмическая функция. Логарифмические уравнения и неравенства", "Производная. Геометрический смысл. Производная сложной функции", "Исследование функций одной переменной".
Контрольные мероприятия
Перед проведением текущих аттестаций выполняются контрольные работы. Контрольные работы направлены на выявление практических навыков в решении задач элементарной математики по рассмотренным темам и усвоения нового материала. Представляют собой билет с 5 задачами.
Контрольная работа № 1.
Планируется на 7 занятии. На ее выполнение отводится 1 час времени.
Контрольная работа № 2.
Планируется на последнем занятии. На ее выполнение отводится 1 час времени.
Требования при подведении итогов текущей и промежуточной аттестаций, определяющие условия, при которых цикл практических занятий считается зачтенным
Дисциплина состоит из курса с практическими занятиями, завершающегося зачетом.
Знания студентов по дисциплине оцениваются по 100-бальной системе со следующими диапазонами баллов:
| Зачет | Не зачтено | Зачтено | ||
| Академическая оценка (по 4-бальной системе) | Неудовлет-ворительно | Удовлет-ворительно | Хорошо | Отлично |
| Бальная оценка (по 100-бальной системе) | От 0 до 39 включи-тельно | От 40 до 60 вклю-чительно | Свыше 60 до 80 вклю-чительно | Свыше 80 до 100 вклю-чительно |
Бальная оценка по дисциплине определяется как сумма баллов, набранных студентом в результате работы в семестре (текущая успеваемость, 60 баллов) и на зачете (промежуточная аттестация, 40 баллов).
Бальная оценка текущей успеваемости складывается из следующих показателей:
· посещаемость — 0-10 баллов (0-5 баллов на каждую аттестацию);
· выполнение контрольной работы № 1 — 0-15 баллов,
· выполнение контрольной работы № 2 — 0-15 баллов,
· выполнение домашних заданий — 0-20 баллов (0-10 баллов на каждую аттестацию).
Отчеты по выполнению самостоятельной работы (домашних заданий) сдаются на проверку дважды в семестре: первый отчет не позднее 31 октября (дня текущей аттестации), второй отчет не позднее зачетной недели. Студенты, не сдавшие отчеты по самостоятельной работе, не допускаются к промежуточной аттестации.
Практические занятия к текущей аттестации будет зачтены при условии выполнения домашних заданий, что подтверждается сдачей отчета по домашним заданиям и набранной балльной оценки не менее 10 баллов.
Цикл практических занятий за семестр считается зачтенным при условии выполнения контрольных работ и сдачи отчетов, содержащих домашние задания.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК.
Основная литература
1. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления: Учебник для вузов. В 3 т. Т.1. — М.: Невский диалект, 2001 .— 680 с.; Т.2. — М.: Невский диалект, 2006 .— 864 с.
2. Кремер Н.Ш., Константинова О.Г., Фридман М.Н. Математика для поступающих в экономические вузы: Учеб. пособие / Под ред. Н.Ш.Кремера. — М.: Юнити-Дана, 2004 .— 605с.
Дополнительная литература
1. Выгодский М.Я. Справочник по элементарной математике. — М.: АСТ: Астрель, 2008.— 509 с.
2. Золотухин А.Я. Элементы теории множеств, меры и интеграла Лебега. Тула: ТулГУ, 2007. – 107с.
3. Иванов К.П. Сборник задач по элементарной математике для абитуриентов. — СПб.: Невский Диалект, 2007. — 336 с.
4. Кузнецов Л.А. Сборник заданий по высшей математике (типовые расчеты). СПб.: Лань, 2008. – 240 с.
5. Симонян, А.З. Математика : Метод.пособие для поступающих в ТулГУ / Симонян А.З.;ТулГУ .— Тула, 2006 .— 112с.
