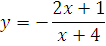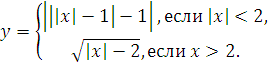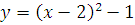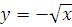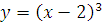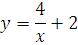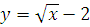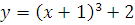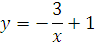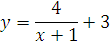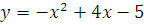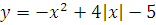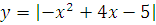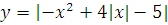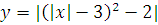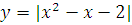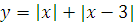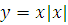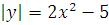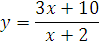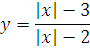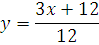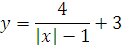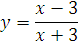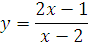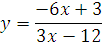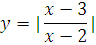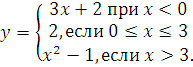Наибольший общий делитель многочленов.
Пусть даны произвольные многочлены 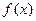 и
и 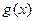 . Многочлен будет называться общим делителем для
. Многочлен будет называться общим делителем для 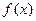 и
и 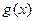 , если он служит делителем для каждого из этих многочленов.
, если он служит делителем для каждого из этих многочленов.
К числу общих делителей многочленов 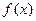 и
и 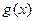 принадлежат все многочлены нулевой степени. Если других общих делителей эти два многочлена не имеют, то они называются взаимно простыми.
принадлежат все многочлены нулевой степени. Если других общих делителей эти два многочлена не имеют, то они называются взаимно простыми.
Наибольшим общим делителем отличных от нуля многочленов 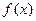 и
и 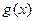 называется такой многочлен
называется такой многочлен 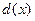 , который является их общим делителем и, вместе с тем, сам делится на любой другой общий делитель этих многочленов.
, который является их общим делителем и, вместе с тем, сам делится на любой другой общий делитель этих многочленов.
Алгоритм Евклида –метод для нахождения наибольшего общего делителя двух целых чисел, а также двух многочленов от одного переменного. Алгоритм Евклида для нахождения наибольшего общего делителя двух многочленов 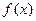 и
и 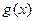 состоит в последовательном делении с остатком
состоит в последовательном делении с остатком 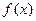 на
на 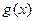 , затем
, затем 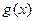 на первый остаток
на первый остаток 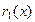 ,затем
,затем 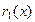 на второй остаток
на второй остаток 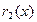 и так далее. Так как степени остатков все время понижаются, то в этой цепочке последовательных делений мы дойдем до такого места, на котором деление совершится нацело и процесс остановится. Последний отличный от нуля остаток
и так далее. Так как степени остатков все время понижаются, то в этой цепочке последовательных делений мы дойдем до такого места, на котором деление совершится нацело и процесс остановится. Последний отличный от нуля остаток 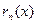 , на который нацело делится предыдущий остаток
, на который нацело делится предыдущий остаток 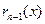 , и является наибольшим общим делителем многочленов
, и является наибольшим общим делителем многочленов 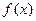 и
и 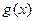 .
.
Наибольший общий делитель двух многочленов определен лишь с точностью до множителя нулевой степени.
Симметрические многочлены от трех переменных.
В многочлене от трех переменных x, y, z перестановок можно сделать три: можно поменять местами x и y, или x и z, или, наконец, y и z. Назовем многочлен ƒ(x, y, z) от трех переменных x, y, z симметрическим, если при любой из этих трех перестановок он остается неизменным:
ƒ(x, y, z)=ƒ(y, x, z)=ƒ(z, y, x)=ƒ(x, z, y).
Наиболее простыми являются симметрические многочлены
x+y+z, xy+xz+yz, xyz.
Их называют элементарными симметрическими многочленами от трех переменных x, y, z и обозначают через 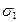 ,
, 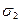 ,
, 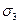 :
:
Основная теорема о симметрических многочленах от трех переменных.
Теорема. Любой симметрический многочлен от x, y, z можно представить в виде многочлена от 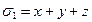 ,
, 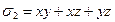 ,
, 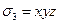 .
.
Основные формулы необходимые для решения задач:
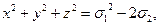
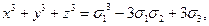
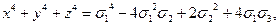
x2y+xy2+x2z+xz2+y2z+yz2= 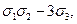
x2y2+x2z2+y2z2= 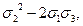
x3y+xy3+x3z+xz3+y3z+yz3= 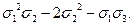
Неприводимый многочлен.
Неприводимый многочлен - это многочлен, не разлагающийся на множители более низкой степени.
Задания.
№ 1. Для каких целых чисел n число 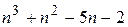 является простым.
является простым.
Решение.
Натуральное число, отличное от 1, называется простым, если оно делится только на 1 и на само себя; целое отрицательное число k называется простым, если число –k простое.
Для ответа на поставленный вопрос заметим, что справедливо равенство
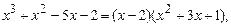
и поэтому число 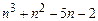 делится на
делится на 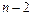 и на
и на 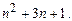 Следовательно, оно может быть простым только в случае, когда один из этих делителей равен 1 или –1, т.е. выполняется хотя бы одно из равенств
Следовательно, оно может быть простым только в случае, когда один из этих делителей равен 1 или –1, т.е. выполняется хотя бы одно из равенств 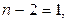
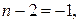
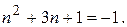
Остается проверить следующие значения n: 3, 1, 0, -3, -1 и –2. При этих значениях n рассматриваемое число равно соответственно 19, -5, 3, 4, так что искомое множество чисел есть 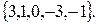
№ 2. Найти частный и остаток от деления 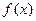 на
на 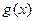 .
.
1. 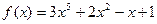 и
и 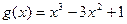
Решение.
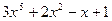 |
| 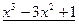
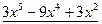
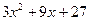
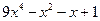
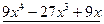
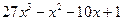
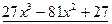

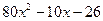
Частным от деления 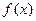 на
на 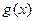 является многочлен
является многочлен 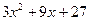 , остатком –
, остатком – 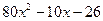 .
.
2. 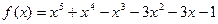 и
и 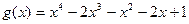
№ 3. Найти наибольший общий делитель многочленов 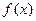 и
и 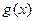 .
.
1. 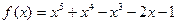 и
и 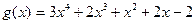
2. 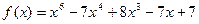 и
и 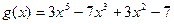
Разделить многочлен f(x) на многочлен g(x):
1. 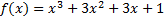 ,
, 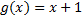 ;
;
2. 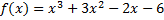 ,
, 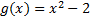 ;
;
3. 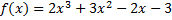 ,
, 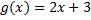 ;
;
Занятие 4.
Тема занятия: «Рациональные уравнения. Корни многочленов. Теорема Безу. Схема Горнера. Кратность корня и производная.»
План занятия.
- Знакомство с теоретическим материалом.
- Разбор заданий под руководством преподавателя.
- Самостоятельное выполнение заданий.
Методические материалы.
Корни многочленов.
Корни многочлена
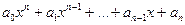
есть корни рационального уравнения
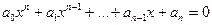
Рациональные уравнения.
Уравнение вида P(x) = 0, где P(x) - рациональная функция, называется рациональным уравнением. Часто рациональное уравнение записывают в виде равенства двух рациональных функций
f(x) = g(x)
Число a называется корнем уравнения f(x) = g(x), если при подстановке его вместо x в уравнение получается верное числовое равенство f(a) = g(a).
Можно выделить следующие методы решения рациональных уравнений:
1. Решение с помощью подстановки, т.е. введением новой переменной. Например, в уравнении aP2(x) + bP(x) + c = 0, где P(x) - многочлен, введем новую переменную y = P(x). Решаем квадратное уравнение ay2 + by + c = 0 относительно y и возвращаемся к решению уравнений P(x) = yi, где yi - решения соответствующего квадратного уравнения.
2. Решение разложением на множители. Если уравнение можно представить в виде P(x)Q(x)=0, где P(x) и Q(x) - рациональные функции, то нужно представить уравнение P(x)Q(x) = 0 в виде совокупности:
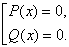
3. Однородное уравнение второго порядка aP2(x) + bP(x)Q(x) + cQ2 (x) = 0. Здесь возможны два случая. Первый - Q(x) = 0, тогда уравнение сводится к решению уравнения P(x) = 0. Второй случай - Q(x) ≠ 0, тогда исходное уравнение можно поделить на Q2 (x) и получить a(P(x)/Q(x)) 2 + bP(x)/Q(x) + c = 0. Вводим замену P(x)/Q(x) = t и получаем квадратное уравнение at2 + bt + c = 0. В ответ включаем решения обоих случаев.
4. Симметричное уравнение третьего порядка: ax3 + bx2 + bx + a = 0. Для его решения проведем следующие преобразования: ax3 + bx2 + bx + a = a(x3 + 1) + bx(x + 1) = a(x + 1)(x2- x + 1) + bx(x + 1) = (x + 1)(ax2 + (b - a)x + a). Решаем совокупность:
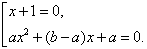
5. Симметрическое уравнение четвертого порядка ax4 + bx3 + сx2 + bx + a = 0. Сгруппируем слагаемые и разделим обе части на x2. Получим a(x2 +1/x2)+ b(x + 1/x) с = 0. Сделаем подстановку x + 1/x = t, тогда x2 + 1/x2 = t2 - 2. Получаем квадратное уравнение at2 + bt + (c - 2a) = 0. После его решения возвращаемся к исходной переменной x.
6. Возвратное уравнение. Уравнение вида ax4 + bx3 + сx2 + dx + e = 0, где a ≠ 0, b ≠ 0 иe/a = (d/b)2, называется возвратным уравнением четвертого порядка. Для его решения делим уравнение на x2 и вводим переменную t = bx + d/x, после чего получаем квадратное уравнение at2/b2 + t + с - 2ad/b = 0. Решив его, возвращаемся к исходной переменной.
7. Уравнения вида (x + a)(x + b)(x + c)(x + d) = m, где a + b = c + d. В даном случае вводим новую переменную t = x2 + (a + b)x и получаем квадратное уравнение (t + ab)(t +cd) = m. Решив его, возвращаемся к исходной переменной.
8. Уравнение вида P(x)/Q(x) = 0. Решаем уравнение P(x) = 0. Проверяем, чему равно значение Q(xi), где xi - корни уравнения P(x) = 0. Если Q(xi) ≠ 0, значит они являются решением исходного уравнения. Если Q(xi) = 0 - корень выпадает из области определения исходного уравнения и его нужно исключить из ответа.
9. Уравнение вида aP(x)/Q(x) + bQ(x)/P(x) + c = 0. Вводим новую переменную t =P(x)/Q(x) и получаем следующее уравнение: at + b/t + c = 0. Или после домножения на t (t ≠ 0) получаем квадратное уравнение at2 + ct + b = 0. Решив его, возвращаемся к исходной переменной.
10. Уравнение состоящее из суммы дробей. Один из методов состоит в том, что нужно перенести все члены уравнения в одну часть и свести уравнение к виду P(x)/Q(x) = 0.
Теорема Безу. Многочлен f(x) делится на x-c тогда и только тогда, когда число c является его корнем.
Кратность корня.
Если c – корень многочлена f(x), может оказаться, что многочлен f(x) делится не только на первую степень линейного двучлена x-c, но и на более высокие его степени. Во всяком случае, найдется такое натуральное число k, что f(x) нацело делится на 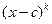 , но не делится на
, но не делится на 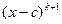 . Поэтому
. Поэтому
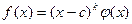 ,
,
где многочлен 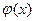 на x-c уже не делится. Число k называется кратностью корня c в многочлене f(x), а сам корень c – k- кратным корнем этого многочлена. Если k=1, то говорят, что корень с – простой.
на x-c уже не делится. Число k называется кратностью корня c в многочлене f(x), а сам корень c – k- кратным корнем этого многочлена. Если k=1, то говорят, что корень с – простой.
Производная от многочлена.
Понятие кратного корня тесно связано с понятием производной от многочлена. Пусть дан многочлен n–ной степени
f(x)= 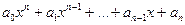
Его производной (первой производной) называется многочлен (n- 1)-й степени
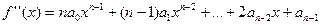
Производная от многочлена нулевой степени и от нуля считается равной нулю.
Для производной k-го порядка справедливо 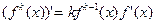
Свойства.
Многочлен 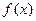 тогда и только тогда не содержит кратных множителей, если он взаимно прост со своей производной.
тогда и только тогда не содержит кратных множителей, если он взаимно прост со своей производной.
Схема Горнера.
Схема Горнера предназначена для вычисления значения полинома в точке. Пусть дан полином
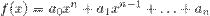
Разделим 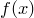 на
на 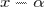 с остатком:
с остатком:
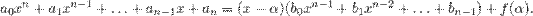
Приравняем коэффициенты при одинаковых степенях 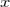 в левой и правой части:
в левой и правой части:
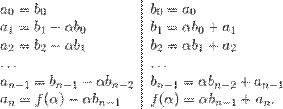
Это можно записать в виде таблицы:
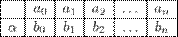
Задания.
№ 1. Решить уравнения, опираясь на теорему Безу.
1. 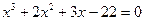
Решение.
Многочлен f(x)= 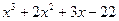 имеет корень 2. По теореме Безу f(x) делится на x-2, то есть имеет место равенство
имеет корень 2. По теореме Безу f(x) делится на x-2, то есть имеет место равенство
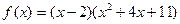 .
.
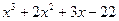 |
| 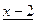
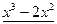
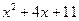
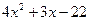
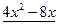
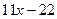
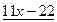
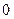
Остается решить квадратное уравнение 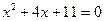 . Это уравнение не имеет действительных корней, так что x=2 – единственный действительный корень исходного уравнения.
. Это уравнение не имеет действительных корней, так что x=2 – единственный действительный корень исходного уравнения.
2. 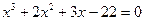
№ 2. Найти производную 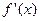 многочлена
многочлена 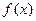 .
.
1. 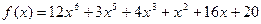
2. 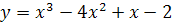
3. 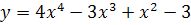
№ 3. Вычислить значение многочлена в точке, используя схему Горнера.
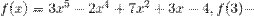
Занятие 5.
Тема занятия: «Рациональные дроби и их разложение на простейшие дроби. Рациональные неравенства.»
План занятия.
- Знакомство с теоретическим материалом.
- Разбор заданий под руководством преподавателя.
- Самостоятельное выполнение заданий.
Методические материалы.
Рациональную дробь вида Pn(x)/Qm(x), где Pn(x), Qm(x) - многочлены порядка n и m соответственно (n<m) можно разложить на элементарные дроби. Алгоритм следующий:
1. Знаменатель Qm(x) разложить на множители вида (x-x0)k, (x2+bx+c) и константу а, где (x-x0)k - множитель соответствующий корню x0 кратности k, (x2+bx+c) - множитель соответствующий случаю двух сопряженных комплексных корней, а=am - коэффициент стоящий при xm многочлена Qm(x).
2. Записать рациональную дробь вида Pn(x)/Qm(x) в виде суммы простейших дробей, у которых неизвестны коэффициенты числителя. Скобкам знаменателя вида (x-x0) соответствует дробь A/((x-x0), скобкам вида (x-x0)k соответствует сумма дробей
В1/(x-x0)+B2/(x-x0)k+...+Bk/(x-x0)k, скобкам вида (x2+bx+c) соответствует дробь
(Cx+D)/(x2+bx+c).
3. Приравниваем исходной дроби Pn(x)/Qm(x) к построенной сумме дробей находят неизвестные коэффициенты в разложении.
Задания.
№ 1. Найти числа a, b, c, при которых следующее равенство справедливо на области допустимых значений этого равенства:
-
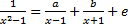 ;
; -
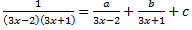 ;
;
№ 2. Разложить рациональную дробь на элементарные дроби.
- (x-1)/(x+1)
- (x^2+3x-3)/(x^3-1)
- x/(x^2-1)
- (x^2+1)/(x^2-1)
- 1/((x+1)^3+1)
Занятие 6.
Тема занятия: «Функция одной переменной. Основные понятия и определения. Элементарные функции и их графики. Преобразования функций.»
План занятия.
- Знакомство с теоретическим материалом.
- Разбор заданий под руководством преподавателя.
- Самостоятельное выполнение заданий.
Методические материалы.
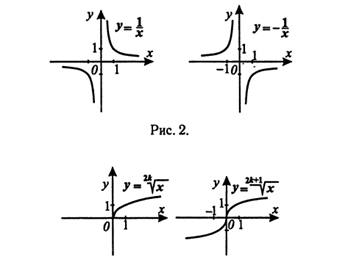
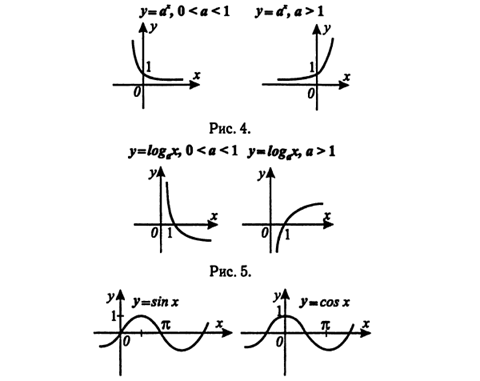
Элементарные функции.
На рисунках 2 — 7 изображены графики основных элементарных функций.
Преобразования функций.
Построение графиков функций «механическими» преобразованиями изображено на нижеследующих рисунках.
График функции у = —f(х) получен из графика функции у = f(х) отражением относительно оси Ох (см. рис. 8). График функции у = f(-х) получен из графика функции у=f(х) отражением относительно оси Оу (см. рис. 9).
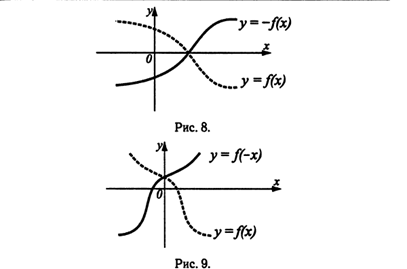
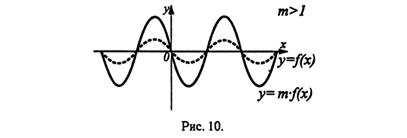
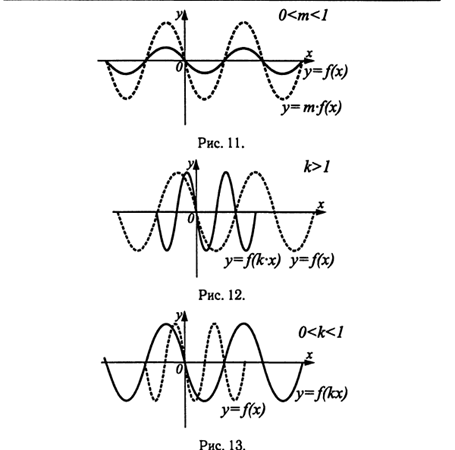
График функции у = m*f(х), m>1, получен из графика функции у = f(x) растяжением в m раз вдоль оси Оу от оси Ох (см. рис. 10). График функции у = m*f(х), 0<m<1, получен из графика функции у = f(x) сжатием в 1/m раз вдоль оси Оу к оси Ох (см. рис. 11).
График функции у = f(kx), k>1, получен из графика функции у = f(х) сжатием в к раз к оси Оу вдоль оси Ох, см. рис. 12. График функции у = f(kx), 0<k<1, получен из графика функции у = f(x) растяжением в 1/k раз от оси Оу вдоль оси Ох, см. рис. 13.
График функции у = f(x) + B получен из графика функции у =f(х) сдвигом вверх на число B при B> 0 и сдвигом вниз на число (-B) при B< О, см. рис. 14. График функции у=f(x+а) получен из графика функции у =f(x) сдвигом вправо на число -а при а < 0 и сдвигом влево на число а при а > 0, см. рис. 15.
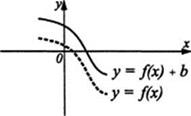
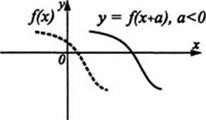
График функции у = |f(x)| (рис. 17) получен из графика функции у = f(x) (рис. 16) отражением относительно оси Ох части этого графика, лежащей ниже оси Ох. График функции у = f(|х|) (рис. 18) получен из графика функции у = f(x) (рис. 16) объединением части этого графика, лежащей правее оси Оу, с её отражением относительно оси Оу и удалением части, лежащей левее оси Оу.
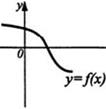
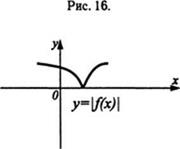
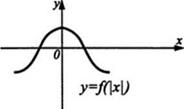
рис. 16 рис. 17. рис. 18
Задания.
Построить графики функций преобразованием от элементарных функций
Занятие 7.
Тема занятия: «Обратная функция. Контрольная работа № 1.»
План занятия.
- Знакомство с теоретическим материалом. Разбор заданий под руководством преподавателя.
- Контрольная работа № 1
Методические материалы.
Функция у = f (х) называется обратимой, если она принимает каждое свое значение один раз.
Пусть f — отображение множества Е на множество М. Если для любого элемента y из множества М существует единственный элемент x — g(y) множества E, для которого F(х) = у, то отображение f называется обратимым. Отображение, обратное к у, обозначают 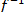 и называют обратной функцией. Функция у = f (х) при этом называется прямой функцией.
и называют обратной функцией. Функция у = f (х) при этом называется прямой функцией.
Областью определения обратной функции является множество значений функции , а множество значений является областью определения функции f.
Функции у = f (х) и х — 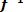 (у) называются взаимно обратными.
(у) называются взаимно обратными.
Для того чтобы некоторая функция имела обратную, необходимо и достаточно, чтобы разным значениям аргумента из области ее определения соответствовали разные значения функции
Контрольная работа № 1
Содержит задачи из разделов: "Множества. Числовые множества. Элементы теории множеств", "Делимость многочленов", "Рациональные уравнения. Корни многочленов", "Рациональные неравенства", "Элементарные функции и их графики", "Преобразования функций", "Обратная функция".
Задания.
№ 1. Задать формулой функцию, обратную данной, указать ее ООФ и МЗФ. Построить их графики:
1. f(x) = 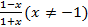
2. 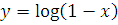
3. 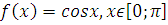
Занятие 8.
Тема занятия: «Основные тригонометрические функции и обратные тригонометрические функции.»
План занятия.
- Разбор заданий контрольной работы № 1, вызвавших наибольшую трудность
- Знакомство с теоретическим материалом.
- Разбор заданий под руководством преподавателя.
- Самостоятельное выполнение заданий.
Методические материалы.
Тригонометри́ческие фу́нкции
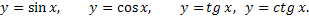
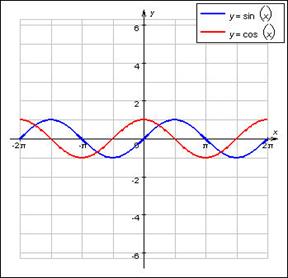
Функция y=sinx. Область определения функции: [-∞,+∞]. Область значения функции [-1,1]. Функция нечетная, периодическая с периодом 2π. Точки пересечения с осью абсцисс: x=nπ(nϵZ), эти точки являются и точками перегиба графика кривой. Функция на [ 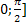 возрастает от 0 до 1 на
возрастает от 0 до 1 на 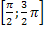 убывает от 1 до -1, на
убывает от 1 до -1, на 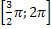 возрастает от -1 до 0. Функция на [
возрастает от -1 до 0. Функция на [ 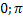 ] выпуклая, а на [
] выпуклая, а на [ 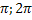 ] вогнутая.
] вогнутая.
Функция y=cosx. Область определения функции: [-∞,+∞]. Область значения функции [-1,1]. Функция четная, периодическая с периодом 2π. Точки пересечения с осью абсцисс: x= 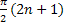 (nϵZ), эти точки являются и точками перегиба графика кривой. Функция на [
(nϵZ), эти точки являются и точками перегиба графика кривой. Функция на [ 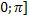 убывает от 1 до -1 на
убывает от 1 до -1 на 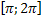 возрастает от -1 до 1. Функция на [
возрастает от -1 до 1. Функция на [ 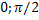 ] выпуклая, а на [
] выпуклая, а на [ 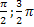 ] вогнутая, [
] вогнутая, [ 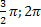 ] выпуклая.
] выпуклая.
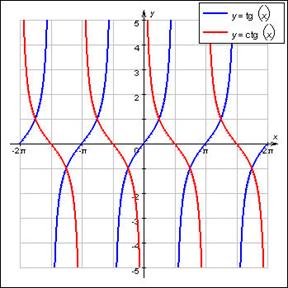
Функция y=tgx. Область определения функции – множество всех действительных чисел, кроме 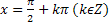 . Область значения [-∞,∞]. Функция нечетная, периодическая с периодом π. Точки пересечения в осью абсцисс:x=kπ
. Область значения [-∞,∞]. Функция нечетная, периодическая с периодом π. Точки пересечения в осью абсцисс:x=kπ 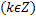 , эти же точки = точки перегиба. Функция на [
, эти же точки = точки перегиба. Функция на [ 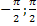 ] возрастает от -∞ до ∞. Функция вогнутая на
] возрастает от -∞ до ∞. Функция вогнутая на 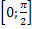 , выпуклая – на
, выпуклая – на 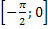 . Вертикальные асимптоты:
. Вертикальные асимптоты: 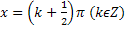 .
.
Функция y=ctgx. Область определения функции – множество всех действительных чисел, кроме 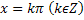 . Область значения [-∞,∞]. Функция нечетная, периодическая с периодом π. Точки пересечения в осью абсцисс:x=k+
. Область значения [-∞,∞]. Функция нечетная, периодическая с периодом π. Точки пересечения в осью абсцисс:x=k+  π
π 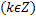 , эти же точки - точки перегиба. Функция на [
, эти же точки - точки перегиба. Функция на [ 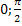 ]убывает от -∞ до ∞. Функция вогнутая на
]убывает от -∞ до ∞. Функция вогнутая на 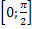 , выпуклая – на
, выпуклая – на 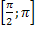 . Вертикальные асимптоты:
. Вертикальные асимптоты: 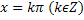 .
.
Графики функций: