Приложения алгебраического вектора
В настоящее время известны два вида материи: вещество и поле. И основным неотъемлемым свойством, способом существования материи является движение. Под движением в общем виде понимается не только перемещение тел в пространстве, но и тепловые, химические, электромагнитные и любые другие изменения и процессы, включая наше сознание и мысль.
Весь курс «Теоретическая механика» и первые разделы физики изучают механическое движение. Материальные тела, с которыми имеют дело в этих дисциплинах, весьма различны, но движение их обладает многими общими свойствами, не зависящими от физических свойств самих движущихся тел. Как известно, материальное тело, размерами которого можно пренебречь в условиях задачи, называется материальной точкой.
Чтобы различать точки в пространстве, применяются системы отсчета с соответствующей системой координат, приборы для измерения длин и времени.
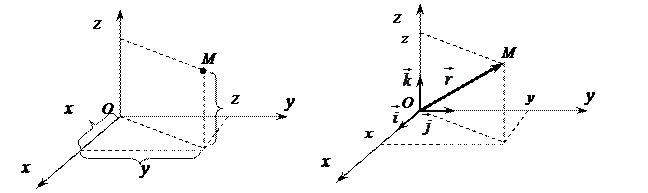
Каждой точке 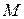 в пространстве ставятся в соответствие три действительных числа
в пространстве ставятся в соответствие три действительных числа 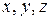 , т.е.
, т.е. 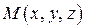 . Каждой точке
. Каждой точке 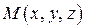 можно поставить в соответствие радиус-вектор с теми же координатами, т.е.
можно поставить в соответствие радиус-вектор с теми же координатами, т.е.
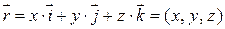 .
.
При движении точки 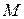 ее координаты изменяются с течением времени
ее координаты изменяются с течением времени 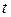 , т.е. координаты будут являться некоторыми функциями аргумента
, т.е. координаты будут являться некоторыми функциями аргумента 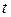 , называемые уравнениями движения:
, называемые уравнениями движения:
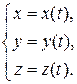
Движение точки 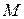 можно описать и радиус-вектором, который непрерывно изменяется, т.е. является векторной функцией времени, называемый векторным уравнением движения:
можно описать и радиус-вектором, который непрерывно изменяется, т.е. является векторной функцией времени, называемый векторным уравнением движения:
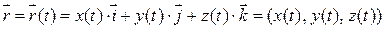 .
.
Таким образом, задание одного векторного уравнения равносильно заданию трех скалярных функций. Вектор-функция изучается в таком разделе как «Дифференциальное исчисление функции».
Одним из основных понятий в динамике механических систем является понятие «центра масс», или «центра инерции системы». Центром масс (или центром инерции) системы называется геометрическая точка C, относительно которой масса системы по всем направлениям распределена одинаково. Радиус-вектор 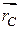 центра масс определяется следующей формулой:
центра масс определяется следующей формулой:
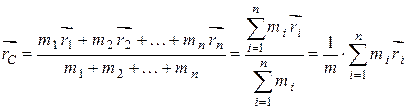 ,
,
где 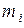 - масса i-ой частицы,
- масса i-ой частицы, 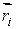 - радиус-вектор, определяющий положение этой частицы, m – масса системы.
- радиус-вектор, определяющий положение этой частицы, m – масса системы.
Декартовы координаты центра масс равны проекциям 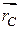 на координатные оси:
на координатные оси:
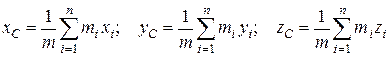 .
.
В частности, если в вершинах треугольника ABD сосредоточены массы 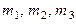 , то радиус-вектор центра масс будет определяться формулой
, то радиус-вектор центра масс будет определяться формулой
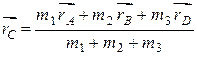 .
.
Если 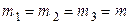 , то радиус-вектор центра масс будет совпадать с центром тяжести треугольника, и расположен в точке пересечения его медиан. В этом случае формула преобразуется к виду
, то радиус-вектор центра масс будет совпадать с центром тяжести треугольника, и расположен в точке пересечения его медиан. В этом случае формула преобразуется к виду
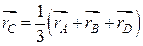 .
.
Пример 2.6. Сила, модуль которой 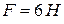 , действует в направлении вектора, образующего с координатами осями
, действует в направлении вектора, образующего с координатами осями 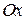 ,
, 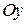 ,
, 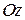 соответствующие углы
соответствующие углы 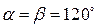 ,
, 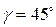 . Найти проекции вектора силы. Записать вектор силы в виде разложения по ортам
. Найти проекции вектора силы. Записать вектор силы в виде разложения по ортам 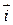 ,
, 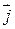 ,
, 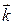 .
.
Решение. Согласно формулам (2.5) имеем
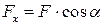 ,
, 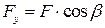 ,
, 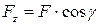 .
.
Тогда
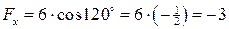 (Н);
(Н);
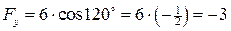 (Н);
(Н);
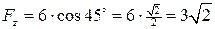 (Н).
(Н).
Вектор силы 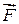 при разложении по ортам координатных осей примет вид:
при разложении по ортам координатных осей примет вид:
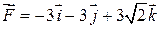 .
.
,
Пример 2.7. Частица 1 столкнулась с частицей 2, в результате чего возникла составная частица. Найти ее скорость 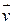 и модуль
и модуль 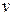 , если масса у частицы 2 в два раза больше, чем у частицы 1, а их скорости перед столкновением равны
, если масса у частицы 2 в два раза больше, чем у частицы 1, а их скорости перед столкновением равны 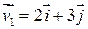 и
и 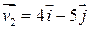 , где компоненты скорости даны в СИ, т.е.
, где компоненты скорости даны в СИ, т.е. 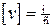 .
.
Решение. Согласно закону сохранения импульса для нашего случая имеем
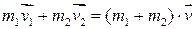 ,
,
где 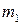 − масса частицы 1;
− масса частицы 1; 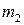 − масса частицы 2;
− масса частицы 2; 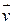 − вектор скорости после соударения.
− вектор скорости после соударения.
По условию 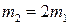 . Тогда
. Тогда
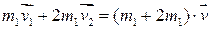 ,
,
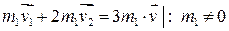 ,
,
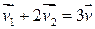 .
.
Выражаем вектор 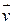 :
: 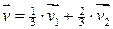
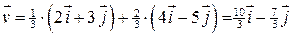 .
.
Находим модуль вектора 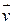 :
: 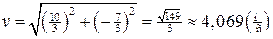 .
.
,
3. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ
3.1. Скалярное произведение и его свойства
Определение 3.1. Скалярным произведением двух ненулевых векторов 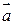 и
и 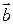 называется число, равное произведению длин этих векторов на косинус угла между ними. Обозначается
называется число, равное произведению длин этих векторов на косинус угла между ними. Обозначается 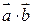 или
или 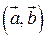 .
.
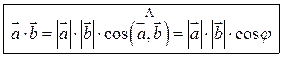 . (3.1)
. (3.1)
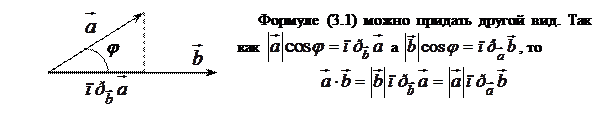
т.е. скалярное произведение двух ненулевых векторов равно произведению модуля одного из них и проекции другого на ось, составленную с первым вектором.
