Оптимальное оценивание сигнала

Оценивание сигнала, как функции времени, – достаточно сложная задача. Во многих случаях ее можно свести к более простой задаче оценивания одного или нескольких параметров сигнала.

Простейшей задачей, связанной с оцениванием параметров сигнала, является оценка параметра, постоянного или настолько медленно меняющегося во времени, что на интервале наблюдения его можно считать постоянным.

Рассмотрим задачу оценивания единственного параметра λ, который до опыта рассматривается как случайная величина, имеющая априорное распределение с плотностью w(λ).

Реализация этой случайной величины представляет собой значение, постоянное на интервале (0, T) наблюдения колебания z(t) = s[t, λ] + ξ(t).

Правило оценивания – это алгоритм обработки наблюдаемого колебания, результатом выполнения которого является значение 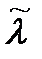оценки параметра λ.

Для оценивания одного и того же параметра может существовать множество алгоритмов, вырабатывающих различные оценки. Для сравнения алгоритмов оценивания между собой и выбора наилучшего используют показатели несмещённость, состоятельность и эффективность.

Несмещенность.Оценка называется несмещенной, если выполняется условие 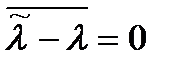, означающее, что при любом значении параметра условное математическое ожидание оценки равно этому значению .

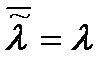Другими словами, несмещенность означает отсутствие систематической ошибки оценивания. В противном случае оценка называется смещенной. Следует отметить, что смещенные оценки также находят применение, если смещение достаточно мало или стремится к нулю при увеличении времени наблюдения или мощности сигнала.

Состоятельность.Оценка называется состоятельной, если при неограниченном возрастании времени наблюдения оценка сходится по вероятности к значению параметра

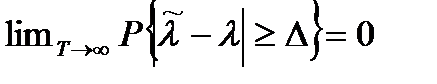, при любом Δ > 0.

(Здесь P{A} обозначает вероятность события A.)

Смещенная оценка может быть состоятельной, если ее смещение стремится к нулю при T → ∞. Следовательно, дисперсия ошибки для состоятельной оценки стремится к нулю

.

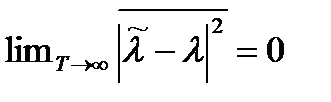Эффективность.Несмещенная оценка называется эффективной, если среди всех оценок, полученных при заданном времени наблюдения всевозможными алгоритмами оценивания, она обеспечивает наименьшую дисперсию ошибки

.

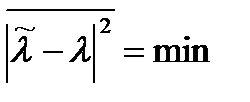Классический подход к оцениванию параметров сигналов основывается на формуле Байеса для апостериорной плотности распределения вероятностей оцениваемого параметра

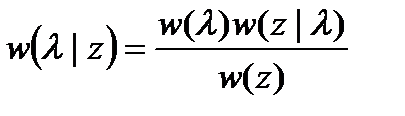, (18.2)

где w(λ) – априорная ПРВ параметра λ; w(λ|z) – условная ПРВ наблюдаемого процесса при заданном значении λ,рассматриваемая как функция от λ при данном z (функция правдоподобия); w(z) – при фиксированной реализации z постоянная величина.

Выражение (18.2) показывает, что, зная априорную плотность w(λ) и наблюдая реализацию процесса z, можно получить уточненное представление о значении параметра λ. На рисунке 18.2 показаны примеры априорной и апостериорной ПРВ параметра (истинное значение параметра обозначено λ₀).

Апостериорное распределение обостряется по сравнению с априорным распределением, т.к., реализация z, содержит дополнительную информацию о параметре, что уменьшает исходную неопределенность априорной ПРВ.

Апостериорное распределение содержит всю информацию о параметре, которую можно получить из наблюдаемой реализации и априорных данных. Поэтому правило оценивания должно использовать апостериорную ПРВ, а способ ее использования зависит от выбранного критерия качества оценки.

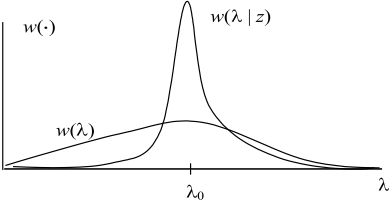
Рис. 18.2. Априорная и апостериорная ПРВ оцениваемого параметра

Ошибки оценивания параметра приводят к различным последствиям, поэтому для их учета вводится функция потерь 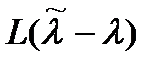,зависящая от разности оценки и истинного значения параметра.

Усредняя функцию потерь по апостериорному распределению параметра, получаем количественную характеристику, называемую апостериорным (условным) риском

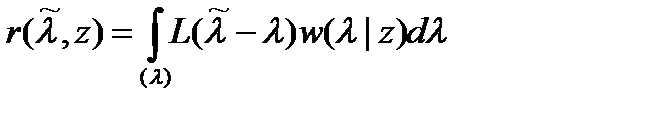, (18.3)

описывающим потери, связанные с получением оценки при наблюдении реализации z. Усреднение апостериорного риска (18.3) по всевозможным реализациям приводит к среднему риску

.

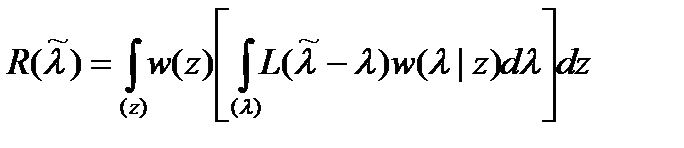Правило оценивания, которому соответствует наименьший средний риск, называется байесовским, а соответствующая оценка – байесовской, или оценкой по критерию минимума среднего риска. Правило, оптимальное в смысле минимума среднего риска, находится из условия минимизации условного риска (18.3).

Часто используют квадратичную функцию потерь 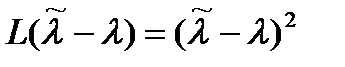,тогда

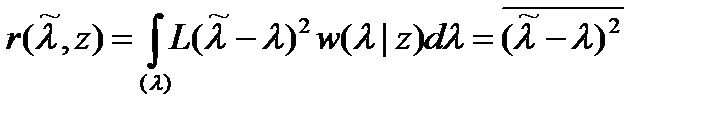, (18.4)

Таким образом апостериорный риск равен среднему квадрату ошибки (а если оценка несмещенная, то дисперсии ошибки). Байесовская оценка в этом случае становится оценкой минимума среднеквадратической ошибки. Для нахождения правила раскроем скобки в выражении (18.4):

.

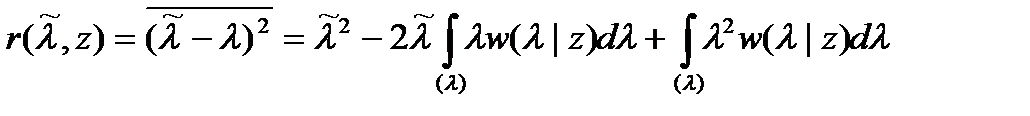Дифференцируя полученное выражение по λ и приравнивая результат нулю, получаем правило

.

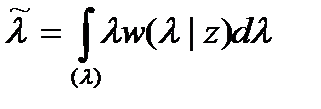Тоесть оценка, оптимальная в смысле минимума среднеквадратической ошибки, равна апостериорному среднему значению параметра.

Кроме квадратичной часто используется простая функция потерь

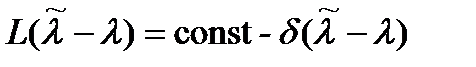, (18.5)

Подставляя (18.5) в (18.4), получаем

.

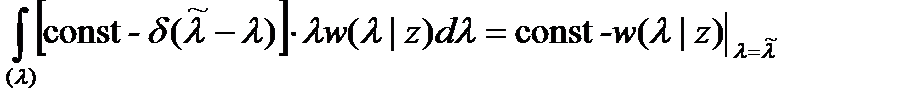Очевидно, что это выражение достигает минимума, если в качестве оценки 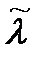использовать значение параметра, доставляющее максимум апостериорной ПРВ w(λ|z). Такая оценка называется МАВ-оценкой (оценкой максимума апостериорной вероятности).

Во многих задачах априорная ПРВ параметра неизвестна, тогда принимают ее равной константе и максимизируют функцию правдоподобия w(λ|z). Получаемые таким образом оценки называются оценками максимального правдоподобия, или МП-оценками.

Пример.Наблюдается колебание z(t) = γs(t) + ξ(t), где s(t) – точно известный сигнал; γ – амплитудный множитель, подлежащий оцениванию; ξ(t) – гауссовский шум с нулевым средним и спектральной плотностью мощности N₀/2, постоянный в полосе частот -F < f < F («квазибелый» шум). Найдем правило оценивания параметра γ, оптимальное по критерию максимального правдоподобия.

Возьмем n отсчетов наблюдаемого колебания на интервале наблюдения Т с шагом Δt = 1/2F = T/n, при этом отсчеты шума являются некоррелированными. Совместная плотность распределения вероятности взятых отсчетов поэтому равна

,

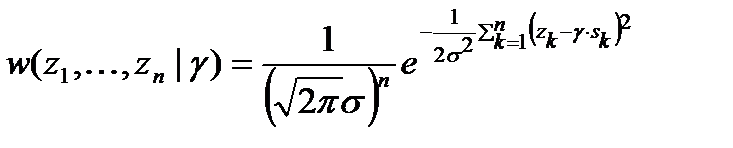где σ² = N₀F = N₀/(2Δt). Устремляя Δt к нулю (n → ∞), запишем функцию правдоподобия

,

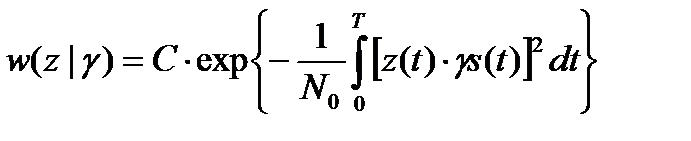где С – константа, несущественная для задачи оценивания.

Для нахождения правила оценивания следует продифференцировать функцию правдоподобия или, что проще, ее логарифм и приравнять результат нулю. Получаемое при этом уравнение правдоподобия 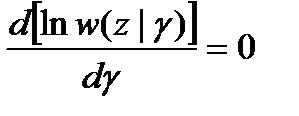для данного случая имеет вид 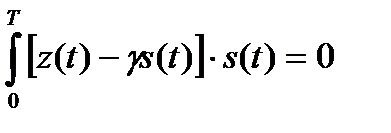,откуда

.

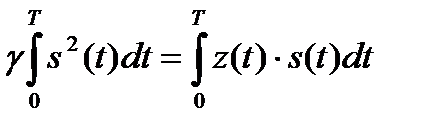Решением этого уравнения относительно γ является оценка 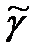, определяемая выражением

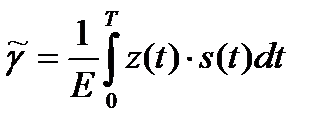, (18.6)

где 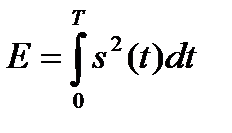– энергия сигнала, известная по условию задачи.

Качество полученной МП-оценки можно оценить, подставив в (18.6) выражение для z(t):

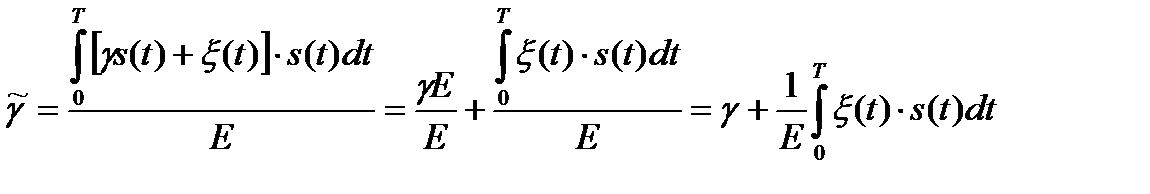. (18.7)

Второе слагаемое представляет собой ошибку оценивания, причем дисперсия интеграла равна N₀E/2, поэтому дисперсия ошибки равна N₀/2E.

Таким образом, оценка тем точнее, чем больше энергия сигнала (для гармонического сигнала s(t) увеличение энергии эквивалентно увеличению длительности интервала наблюдения) и чем меньше спектральная плотность мощности помехи. Из выражения (18.7) видно, что оценка несмещенная, так как ξ(t) имеет нулевое математическое ожидание. Учитывая несмещенность и стремление дисперсии к нулю при увеличении интервала наблюдения, можно заключить, что оценка является состоятельной. Кроме того, можно показать, что оценка также эффективна.

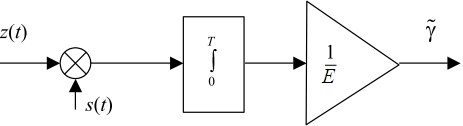
Рис. 18.3. Структура устройства оценивания амплитуды сигнала