Синтез БИХ-фильтров на основе аналого-цифровой трансформации

Сравнение БИХ-фильтров с КИХ-фильтрами показывает, что для получения примерно одинаковых частотно-избирательных свойств (имеется в виду крутизна спада АЧХ) КИХ-фильтр должен иметь в 10…20 раз более высокий порядок. Это вполне объяснимо, так как известно, что быстро изменяющиеся сигналы имеют широкий спектр, а благодаря двойственности (дуализму) времени и частоты отсюда следует, что круто изменяющейся функции частоты (АЧХ) должна соответствовать функция времени (импульсная характеристика) большой длительности. Но для КИХ-фильтра порядок – это количество отсчетов импульсной характеристики минус 1, в то время как БИХ-фильтр даже первого порядка имеет импульсную характеристику бесконечной длительности. Таким образом, в тех случаях, когда вид фазочастотной характеристики не играет определяющей роли для практического применения разрабатываемого фильтра, следует использовать БИХ-фильтр, так как при этом получается существенный выигрыш в быстродействии (или в аппаратурных затратах на реализацию) фильтра. То обстоятельство, что не всякий БИХ-фильтр оказывается устойчивым, не представляет такой заметной опасности, как может показаться на первый взгляд. Во-первых, устойчивость может быть проверена (и обеспечена) на этапе проектирования цифрового фильтра; во-вторых, характеристики цифровых фильтров не подвержены дрейфу с течением времени и при изменении внешних условий, следовательно, устойчивый фильтр останется устойчивым в течение всего времени работы (конечно, нужно учитывать возможность выхода аппаратуры из строя в результате катастрофического отказа; при этом может возникнуть неустойчивость). Следует также отметить, что в цифровых БИХ-фильтрах могут возникать незатухающие паразитные колебания (так называемые предельные циклы) вследствие своеобразного нарушения устойчивости при округлении дробных чисел; подробнее см. [7].

Наиболее широко применяются методы синтеза цифровых БИХ-фильтров, основанные на так называемой аналого-цифровой трансформации, т.е. на преобразовании аналогового фильтра с требуемыми характеристиками в цифровой (дискретный) фильтр.

Это объясняется, во-первых, трудностью решения задачи прямой аппроксимации желаемых характеристик дробно-рациональными передаточными функциями и, во-вторых, наличием развитой теории синтеза аналоговых фильтров и простотой преобразования аналоговых фильтров-прототипов в дискретные фильтры.

В качестве фильтров-прототипов наиболее часто применяются аналоговые фильтры Баттерворта, Чебышева, Золотарева-Кауэра (эллиптические) и Бесселя. Фильтры Баттерворта имеют при заданном порядке максимально гладкую АЧХ. Фильтры Чебышева имеют АЧХ, пульсирующую в полосе пропускания (фильтры I рода) или в полосе заграждения (фильтры II рода). АЧХ эллиптического фильтра пульсирует как в полосе пропускания, так и в полосе заграждения и поэтому имеет максимальную крутизну спада.

Все перечисленные фильтры характеризуются заметной нелинейностью фазочастотной характеристики. Фильтр Бесселя имеет ФЧХ, близкую к линейной в полосе пропускания.

Аналоговые фильтры принято описывать передаточными функциями, которые связаны с импульсными характеристиками преобразованием Лапласа [8]. Преобразование Лапласа связывает аналоговый сигнал x(t) с его образом (изображением) в виде функции X(p) комплексного переменного p. Мнимая ось комплексной p-плоскости представляет собой ось частот в описании аналогового сигнала. Аналогичную роль в описании дискретных сигналов играет единичная окружность z-плоскости.

Аналого-цифровая трансформация состоит в установлении связи комплексных переменных p и z. Выразив p в виде функции p = f(z) и подставив в выражение передаточной функции H_a(p) аналогового фильтра-прототипа, мы получили бы функцию комплексного переменного z, имеющую смысл передаточной функции H(z) дискретного фильтра. Трудность состоит в том, что, во-первых, мнимая ось p-плоскости имеет бесконечную, а единичная окружность z-плоскости – конечную длину 2π. Во-вторых, реализуемы только ЛИС-цепи конечного порядка, поэтому подстановка p = f(z) в дробно-рациональную функцию H_a(p) должна давать также дробно-рациональную функцию.

Поскольку на единичной окружности z = e^jω, а при дискретизации должно обеспечиваться равенство ω = ΩT_d, связь комплексных переменных p и z, обусловленная дискретизацией аналоговых сигналов, описывается выражениями

z = exp(pT_d) (13.4)

и

p = ln z / T_d , (13.5)

которые не являются дробно-рациональными. Различные способы преодоления этой трудности лежат в основе двух рассмотренных ниже методов аналого-цифровой трансформации.

Метод инвариантности импульсной характеристики.

Передаточная функция произвольного аналогового фильтра (с сосредоточенными параметрами) имеет вид дробно-рациональной функции комплексного переменного p. Такая функция может быть представлена в виде суммы дробей

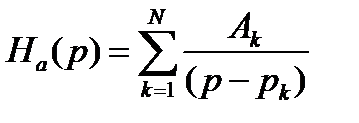
где p_k, 1 ≤ k ≤ N – полюсы передаточной функции, а коэффициенты A_k определяются из условия равенства числителя передаточной функции H_a(p) и числителя правой части после приведения ее к общему знаменателю. (Здесь мы рассматриваем лишь практически важный случай, когда степень числителя H_a(p) меньше степени знаменателя, а все корни знаменателя некратные.)

Ввиду линейности преобразования Лапласа импульсная характеристика такого фильтра имеет вид суммы экспоненциальных функций непрерывного времени 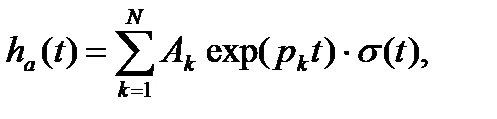σ(t) – функция Хевисайда.

Очевидно, для того чтобы импульсная характеристика затухала со временем (т. е. фильтр был устойчивым), необходимо и достаточно, чтобы все полюсы были расположены в p-плоскости слева от мнимой оси.

Метод аналого-цифровой трансформации, известный под названием метода инвариантности импульсной характеристики, основан на прямом применении теоремы отсчетов (теоремы Котельникова). Рассматривая импульсную характеристику аналогового фильтра-прототипа как функцию времени (сигнал), можно заменить ее последовательностью отсчетов, выбранных с достаточно малым шагом дискретизации T_d.

Результатом дискретизации импульсной характеристики аналогового фильтра будет последовательность

,

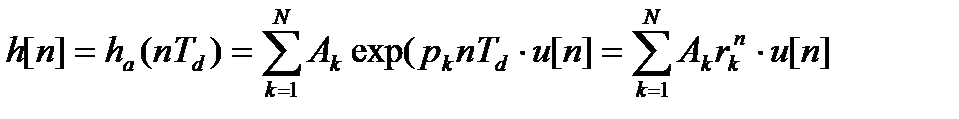где r_k = exp(p_kT_d) – полюсы передаточной функции цифрового фильтра, u[n] который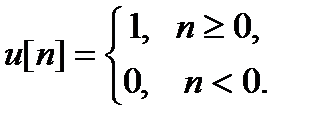

Из полученного выражения видно, что при дискретизации импульсной характеристики каузального аналогового фильтра с дробно-рациональной передаточной функцией получается сумма каузальных экспоненциальных последовательностей, следовательно, реализуемому аналоговому фильтру соответствует реализуемый цифровой фильтр. Кроме того, полюсы цифрового фильтра связаны с полюсами фильтра-прототипа соотношением r_k = exp(p_kT_d), 1 ≤ k ≤ N, поэтому устойчивому аналоговому фильтру (Re{p_k} < 0) соответствует устойчивый цифровой фильтр того же порядка N (так как |r_k| = |exp(p_kT_d)|< 1). Зная полюсы цифрового фильтра, можно сразу записать его передаточную функцию

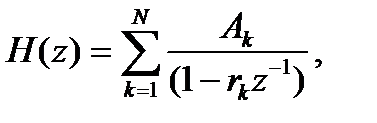
и на этом аналого-цифровая трансформация заканчивается, так как, зная передаточную функцию, легко составить структурную схему и разностное уравнение цифрового фильтра.

Поскольку импульсная характеристика цифрового фильтра есть продукт дискретизации импульсной характеристики аналогового фильтра, КЧХ цифрового фильтра связана с КЧХ аналогового фильтра соотношением

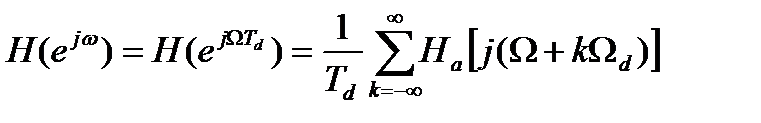, (13.6)

где Ω_d = 2π/T_d – частота дискретизации. Очевидно, если КЧХ прототипа не финитна, а это всегда так для фильтров конечного порядка, то неизбежно наложение (суммирование) «хвостов» сдвинутых копий H_a(•), и, как следствие, искажение формы получаемой КЧХ дискретного фильтра по отношению к КЧХ фильтра-прототипа. Этот эффект ограничивает практическое применение метода инвариантности импульсной характеристики в основном задачами синтеза цифровых фильтров нижних частот.

Метод билинейного преобразования основан на аппроксимации выражения (13.5), позволяющей сохранить дробную рациональность передаточной функции. Подставив разложение функции логарифма в ряд, ограниченное первым слагаемым, получим

,

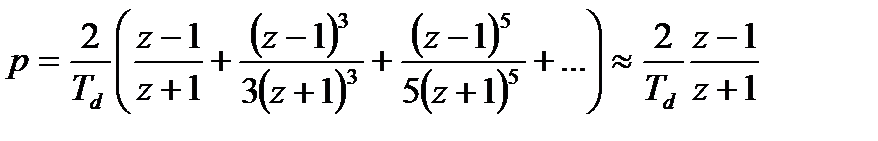или

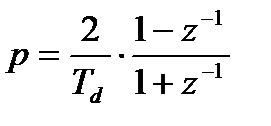. (13.7)

Это выражение дробно-рационально относительно z^-1 поэтому после его подстановки в дробно-рациональную передаточную функцию H_a(p) аналогового прототипа получается снова дробно-рациональная, а следовательно, реализуемая передаточная функция H(z) цифрового фильтра.

Выясним, как располагаются в z-плоскости полюсы передаточной функции H(z), если полюсы передаточной функции прототипа H_a(p) находятся в левой части комплексной плоскости (иными словами, является ли устойчивым цифровой фильтр, если устойчив фильтр-прототип).

Выразим на основе (13.7) комплексное переменное z через p:

z^-1pT_d + pT_d = 2 - 2 z^-1;

отсюда

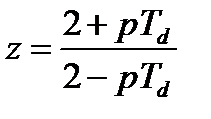. (13.8)

Чтобы выяснить, в какое множество z-плоскости отображается мнимая ось p-плоскости (ось частоты), подставим в это выражение jΩ вместо p, тогда получим выражение для образа мнимой оси p-плоскости при отображении, описываемом выражением (13.8):

.

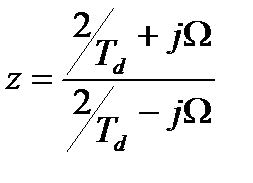Числитель и знаменатель этой дроби суть комплексно-сопряженные числа, поэтому модуль дроби равен единице при всех Ω. Это означает, что мнимая ось p-плоскости отображается преобразованием (13.8) на единичную окружность z-плоскости. Но переменная Ω – это частота, соответствующая описанию аналогового фильтра; роль частотной оси для цифровых цепей играет единичная окружность на z -плоскости (множество точек e^jω при значениях ω, принимающих значения из интервала от -π до π). Заменяя z на e^jω, получим

.

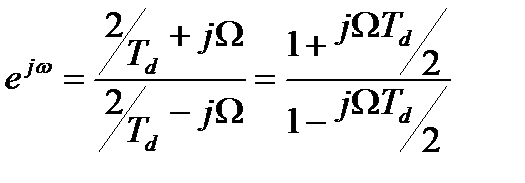Тогда

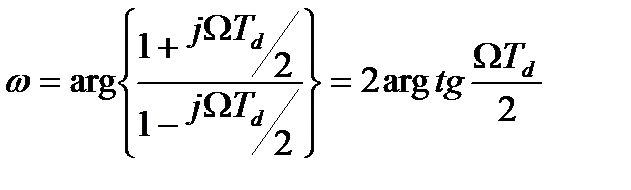
следовательно, связь «аналоговой» и «цифровой» частот при билинейном преобразовании описывается выражениями

ω/2 = argtg(ΩT_d/2),

ΩT_d/2 = tg ω/2. (13.9)

Поскольку π ≤ ω ≤ -π, а -∞ < Ω < ∞, нетрудно видеть, что вся аналоговая частотная ось (бесконечной длины) отображается на единичную окружность (длины 2π), причем это отображение однократно в отличие от (13.6), и вследствие этого различные участки оси Ω испытывают различное «сжатие» при отображении на ось ω (единичную окружность). Это необходимо учитывать при проектировании цифровых фильтров на этапе определения требований к частотам среза фильтров-прототипов.

Заслуживает внимания вопрос, насколько вредна нелинейная трансформация частотной оси с точки зрения задачи синтеза цифровых фильтров. Очевидно, что при проектировании фильтров с желаемыми АЧХ кусочно-постоянного вида указанная нелинейность трансформации частотной оси не влияет на качество цифрового фильтра, так как приводит лишь к необходимости на этапе построения аналогового фильтра-прототипа учитывать последующее изменение характерных частот фильтра (граничных частот) при билинейном преобразовании. Если же требуется построить фильтр, не являющийся типовым (ФНЧ, ФВЧ, полосовым или режекторным), то в общем случае нелинейность отображения частотной оси приводит к искажению формы АЧХ. Например, интегрирующий аналоговый фильтр имеет амплитудно-частотную характеристику гиперболического вида ~1/ Ω и при билинейном преобразовании не приводит к интегрирующему цифровому фильтру.

Для того чтобы устойчивый аналоговый фильтр трансформировался в устойчивый же цифровой фильтр, требуется, чтобы при билинейном преобразовании левая полуплоскость p-плоскости отображалась внутрь единичной окружности. Разлагая p на мнимую и вещественную части, получим для билинейного преобразования (13.8)

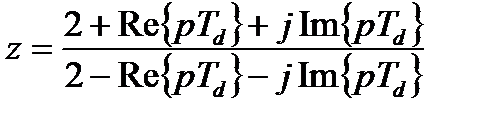
Поскольку мнимые части числителя и знаменателя одинаковы, модуль дроби будет меньше 1, если Re(pT_d) < 0. Тогда любой полюс функции H_a(p), лежащий слева от мнимой оси, отображается в полюс функции H(z), расположенный внутри единичной окружности. Это означает, что устойчивый аналоговый фильтр трансформируется преобразованием (13.7) в устойчивый дискретный фильтр.

Итак, установлено, что билинейное преобразование трансформирует устойчивый реализуемый аналоговый фильтр в устойчивый реализуемый цифровой фильтр. При этом вследствие однократности отображения частотной оси на единичной окружность отсутствует наложение «хвостов» КЧХ, что является достоинством билинейного преобразования. К недостаткам следует отнести то, что не сохраняются ни импульсная, ни фазочастотная характеристики фильтра (точнее говоря, импульсная и фазочастотная характеристики дискретного фильтра могут сильно отличаться по форме от соответствующих характеристик прототипа).

Порядок расчета цифрового фильтра методом билинейного преобразования состоит в следующем:

1) определение характерных частот ЦФ и пересчет их в частоты аналогового фильтра в соответствии с (13.9);

2) синтез аналогового фильтра, удовлетворяющего заданным условиям;

3) подстановка формулы (13.7) билинейного преобразования в выражение H_a(p) передаточной функции фильтра-прототипа.

Реализация цифровых фильтров (и других алгоритмов цифровой обработки сигналов) возможна на различной элементной базе.

Выбор конкретного воплощения алгоритма ЦОС производится разработчиком с учетом различных показателей, к которым относятся стоимость, массогабаритные характеристики, энергопотребление, быстродействие и т.п. В каждом конкретном случае один или несколько показателей играют наиболее важную роль в выборе способа реализации. Например, в системах подвижной радиосвязи главными показателями являются быстродействие (обработка должна выполняться в реальном времени) и массогабаритные характеристики, при этом желательно обеспечить малое энергопотребление и умеренную цену мобильной станции. Устройство обработки сигналов в таких системах работает по жестким алгоритмам, которые не изменяются в течение всего срока эксплуатации изделия; точность представления данных (разрядность) должна быть достаточна для обеспечения комфортности восприятия речи (разборчивости и возможности узнавания собеседника) и является поэтому сравнительно невысокой. В системах обработки геофизической информации, напротив, обработка в реальном времени не требуется, массогабаритные характеристики не играют доминирующей роли, однако на передний план выступают точность представления данных и гибкость реализуемых алгоритмов.

Поэтому в таких системах обработка сигналов реализуется обычно на универсальных цифровых вычислительных машинах. В системах реального времени (например, в подвижной радиосвязи), когда на обработку отсчета сигнала отводится временной интервал, равный шагу дискретизации, как правило, используются специализированные цифровые устройства, называемые цифровыми сигнальными процессорами (ЦСП). Следует отметить, что в последнее время в устройствах цифровой обработки сигналов широкое распространение получили программируемые логические интегральные схемы (ПЛИС). ПЛИС представляет собой интегральную схему сверхвысокой степени интеграции, содержащую на кристалле порядка 1 миллиона логических вентилей, которые могут быть программным путем соединены в логическую структуру, реализующую заданный алгоритм цифровой обработки сигналов аппаратным способом. Таким образом, ПЛИС сочетают в себе преимущества аппаратной реализации алгоритмов (главное из которых – быстродействие) с достоинствами программируемых устройств.

КАНАЛЫ СВЯЗИ

КАНАЛЫ ЭЛЕКТРИЧЕСКОЙ СВЯЗИ

14.1. Основные определения

В общем случае под каналом связи понимают всю совокупность технических средств, обеспечивающих передачу электрических сигналов от источника сообщений к потребителю.

Каналы связи классифицируют по различным признакам:

- по назначению;

- по характеру линий связи;

- по диапазону частот;

- по характеру сигналов на входе и выходе каналов и т. п.

В теории передачи сигналов каналы классифицируют по характеру сигналов на входе и выходе и различают:

- непрерывные;

- дискретные;

- дискретно-непрерывные каналы.

В непрерывных каналах сигналы на входе и выходе непрерывны по уровням;

в дискретных каналах – они соответственно дискретны;

а в дискретно-непрерывных – сигналы на входе дискретны, а на выходе непрерывны, и наоборот.

Возможна также классификация каналов по

- назначению: телеграфные, телефонные, телевизионные, телеметрические и др.;

- виду физической среды распространения: проводные, кабельные, волноводные и др.;

- и диапазону используемых ими частот (таблицы 14.1, 14.2).

К радиодиапазону относят частоты в пределах 30 ... 30·10¹² Гц, что соответствует длинам волн от 10⁸ м до 0,1 мм.

Кроме радиодиапазона, в настоящее время широкое распространение нашел и оптический диапазон волн.

В силу дискретного характера электромагнитного излучения в оптическом диапазоне волн такие каналы принято называть квантовыми.

Таблица 14.1

Частотные диапазоны проводных каналов связи

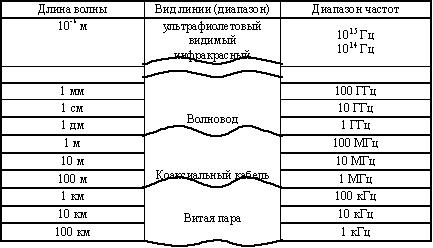
Таблица 14.2

Частотные диапазоны радиоволн

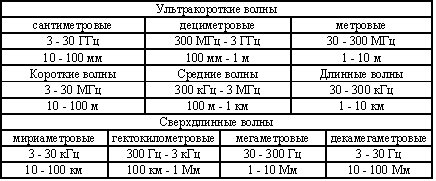
По способу распространения радиоволн различают каналы: с открытым и с закрытым распространением.

В каналах с закрытым распространением электромагнитная энергия распространяется по направляющим линиям (кабельные, проводные, волноводные СВЧ тракты и др.): для них характерны малый уровень помех и постоянство параметров сигнала, что позволяет передавать информацию с высокой скоростью и достоверностью.

Особенности использования радиоволн различных диапазонов в каналах с открытым распространением состоят в следующем. В диапазонах инфранизких (ИНЧ), очень низких (ОНЧ) и низких (НЧ) частот на небольших расстояниях поле в месте приема создается за счет дифракционного огибания волнами выпуклой поверхности Земли. На больших расстояниях радиоволны распространяются в своеобразном сферическом волноводе, внутренняя стенка которого образуется поверхностью Земли, а внешняя – ионосферой. Особенностью этих диапазонов является также способность волн проникать в толщу Земли и воды на глубину в десятки метров.

Принципиальным недостатком таких каналов являются: ограниченная полоса частот (единицы герц) и очень большие линейные размеры антенных устройств, соизмеримых с длиной волны, составляющей километры.

Сверхдлинные волны применяются для навигации и передачи информации на подводные объекты.

В распространении волн диапазона высоких частот (ВЧ) принимает участие ионосфера: если волны длиннее 1 км отражаются от нижнего ее слоя практически зеркально, то декаметровые волны достаточно глубоко проникают в ионосферу, что приводит к эффекту многолучевости, когда в точку приема приходят одновременно несколько сигналов с различным временем запаздывания.

Декаметровые волны широко применяются для глобальной связи и радиовещания. С их помощью можно передавать информацию сравнительно большого объема в пределах всего земного шара при ограниченной мощности передатчика и небольших по размеру антеннах. Полоса частот передаваемых сигналов в декаметровом канале не превышает десяти килогерц.

До появления спутниковых систем связи этот диапазон был единственным пригодным для организации связи между двумя любыми пунктами на Земле без промежуточной ретрансляции.

Гектометровые волны днем распространяются как земные, а ночью – как ионосферные. Дальность распространения земной волны над сушей не превышает 500 км, а над морем – 1000 км. Диапазон средних частот широко используется в радиовещании, связи и радионавигации.

Волны диапазона частот от 30 МГц и выше слабо дифрагируют и поэтому распространяются в пределах прямой видимости. Некоторого увеличения дальности можно достичь, применив поднятые антенны, а для организации связи на расстояния, превышающие прямую видимость, ретрансляцию сигналов. Системы с ретрансляцией сигналов называются радиорелейными линиями.

Одним из основных достоинств высокочастотных диапазонов является большой частотный ресурс, что позволяет создавать радиосистемы передачи информации с высокой скоростью передачи и радиосети с большим числом одновременно работающих радиостанций.

Диапазон миллиметровых волн. Его особенностью является сильное поглощение радиоволн в дожде и тумане, что ограничивает их применение в наземных системах большой дальности. Однако в космических и спутниковых системах они весьма перспективны.

Диапазон рабочих частот 40 МГц ... 40 ГГц (спутниковая связь). В настоящее время наибольшее использование находит диапазон 1 ... 12 ГГц.

Обычно ИСЗ находятся на высоте от 500 до 40 000 км от поверхности Земли и поэтому обеспечивают радиосвязь между земными станциями, удаленными на расстояния до 10 ... 17 тыс. км.

Длина волн 0,5 ... 10,6 мкм, диапазон оптической связи (видимый 0,5 ... 0,76 мкм и инфракрасный 0,76 ... 10,6 мкм участки спектра электромагнитных колебаний).

Широкая полоса частот оптических каналов связи позволяет создавать каналы и сети связи с огромной пропускной способностью.

Представляет интерес классификация каналов телекоммуникаций по характеру сигналов на входе и выходе. Обычно различают:

- непрерывные каналы, на входе и выходе которых сигналы аналоговые (непрерывные по уровням);

- дискретные каналы, на выход которых поступают дискретные по уровням сигналы, и с выхода также снимаются дискретные сигналы;

- дискретно-непрерывные или полунепрерывные, т. е. дискретные каналы со стороны входа и непрерывные со стороны выхода или наоборот.

Совокупность технических средств, включенных между модулятором и демодулятором (рис. 14.1), т.е. выходные каскады передатчика, передающая антенна, среда распространения, приемная антенна и линейная часть приемника, образуют непрерывный канал, так как входные и выходные радиосигналы непрерывны по своей природе.

Рассматривая часть системы между выходом кодера и входом декодера, получим дискретный канал.

Наконец, часть системы между выходом кодера и входом демодулятора образует дискретно-непрерывный канал.

Таким образом, дискретный канал содержит дискретно-непрерывный, который в свою очередь включает в себя непрерывный канал.

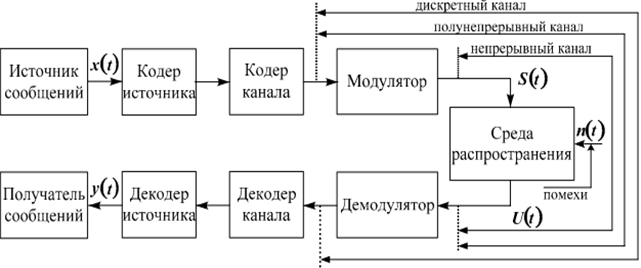
Рис. 14.1. Структурная схема системы электрической связи

Модели непрерывных каналов

Непрерывными называются каналы, входные и выходные сигналы которых принимают произвольные значения из некоторого интервала.

Непрерывные каналы можно классифицировать по виду помех и характеру преобразования входного сигнала S_p(t,λ₀) в полезный принятый S_p(t,λ). Если ограничиться предположением, что в канале действует аддитивный нормальный белый шум n(t), то непрерывные каналы подразделяются по виду преобразования S_p(t,λ₀) в S_p(t,λ), т.е. по виду искажений сигнала. В большинстве радиотехнических систем излученные сигналы являются узкополосными:

S_p(t,λ₀) = A(t) cos[ω₀t + φ(t)],

где A(t) и φ(t) – функции, отображающие законы амплитудной и угловой модуляции; ω₀ – несущая частота сигнала.

Искажения излученного сигнала S_p(t,λ₀) принято рассматривать отдельно для однолучевых и многолучевых каналов. В однолучевых каналах электромагнитные колебания распространяются по одному пути. Однолучевыми каналами являются линии связи на расстояниях прямой видимости: линии ближней радиосвязи на коротких и ультракоротких волнах, линии связи Земля-воздух, воздух-Земля, воздух-воздух и т. п.

Принятый полезный сигнал по отношению к излученному характеризуется дополнительными параметрами: случайным ослаблением α(t), средним временем запаздывания τ_з, доплеровским смещением частоты Ω и случайной начальной фазой θ и может быть записан в виде

S_p(t,λ) = α(t) A(t - τ_з) cos[(ω₀ + Ω)t + φ(t - τ_з) - θ].

Таким образом, совокупность параметров принятого сигнала λ = {A(t), φ(t), ω₀, α(t), τ_з, Ω, θ}. Зная значения дополнительных параметров α(t), τ_з, Ω, θ на приемной стороне, можно выделить несколько моделей непрерывных каналов [2, 9].

Гауссовским каналом называется канал, в котором действует аддитивный нормальный белый шум, а искажения полезного сигнала несущественны и могут быть скомпенсированы. Компенсация искажений возможна, если на приемной стороне дополнительные параметры полностью известны или могут быть измерены достаточно точно. Поэтому можно считать, что S_p(t,λ₀) = S_p(t,λ). Выходной сигнал гауссовского канала

Y_p(t) = S_p(t,λ₀) + n(t).

Представление выходного сигнала в виде суммы полезного сигнала и нормального белого шума n(t) позволяет указать правило принятия решения о переданном сигнале.

Гауссовский канал с неизвестной фазой сигнала определяется параметрами τ_з, Ω, α(t) = α, которые постоянны и известны. Фаза θ считается равномерно распределенной величиной в интервале 0 ÷ 2π. Такая модель хорошо описывает процессы в линиях радиосвязи на расстояниях прямой видимости.

Канал с амплитудными замираниями является дальнейшим усложнением канала с неизвестной фазой в предположении, что α(t) – случайная функция времени. Выходной полезный сигнал канала с замираниями

S_p(t,λ) = α(t) A(t) cos[(ω₀ + Ω)t + φ(t) - θ].

Случайная функция α(t) перемножается с сигналом и поэтому называется мультипликативной помехой, которую можно рассматривать как функцию, модулирующую по амплитуде излученный сигнал. Модуляция приводит к расширению спектра принятого сигнала относительно спектра излученного сигнала. Поэтому такой канал называют каналом с рассеянием энергии по частоте.

По времени корреляции мультипликативные помехи разделяются на медленные и быстрые [10]. О медленных замираниях говорят в случае, если время корреляции α(t) значительно превышает интервал наблюдения сигнала. Причинами медленных замираний являются изменения свойств среды распространения радиоволн в зависимости от метеорологических условий, времени суток и года, от солнечной активности и т. п. Быстрая мультипликативная помеха имеет время корреляции меньшее, чем интервал наблюдения сигнала. Основной причиной быстрых замираний является наличие многих путей, по которым распространяются электромагнитные волны. Многолучевое распространение возникает при передаче информации на дальние расстояния при отражении радиоволн от протяженных поверхностей суши и моря, при отражении от ионосферы и тропосферы. Из-за разных путей распространения время запаздывания отдельных принимаемых сигналов различно. Поэтому многолучевые каналы называют также каналами с рассеянием энергии во времени.

Результирующий сигнал на выходе многолучевого канала

,

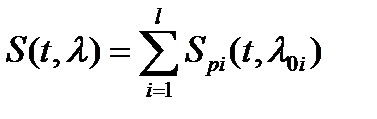где S_pi(t,λ_0i) = α_i(t) A(t) cos[(ω₀ + Ω)t + φ(t) - θ].

При большом числе путей можно считать, что S_p(t,λ) является реализацией нормального СП. Обычно среднее значение процесса равно нулю, тогда модели многолучевых каналов различаются по виду КФ [11].

Таким образом, непрерывный канал считается заданным, если указаны мощность сигналов, полоса частот, дано описание моделей помех и искажений сигналов.

Модели дискретных каналов

Дискретными называются каналы, входные и выходные сигналы которых принимают конечное число мгновенных значений. Понятие дискретного канала естественно возникает при передаче дискретных сообщений и определяется как совокупность технических средств, включенных между кодером и декодером канала (рис. 14.1).

Переход от дискретных сигналов к непрерывным осуществляется на передающей стороне при манипуляции параметрами непрерывной несущей. На приемной стороне дискретные сигналы появляются на выходе первой решающей схемы (демодулятора).

Свойства дискретного канала определяются непрерывным каналом и структурой модема. Дискретный канал задается множеством входных {s_i}, 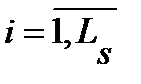и выходных {y_j}, 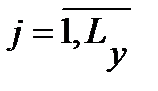символов (сигналов), длительностью символов τ и условными вероятностями P(y_j/s_i) преобразования входных символов в выходные. Обычно длительности всех входных и выходных символов одинаковы. Объемы алфавитов входных L_s и выходных L_y сигналов в общем случае могут быть разными, причем L_y ≥ L_s. Однако в большинстве случаев L_y = L_s. Для дискретных каналов широко используется представление принятой последовательности символов Y = (y₁, y₂,..., y_n) в виде суммы переданной последовательности S = (s₁, s₂,..., s_n) и комбинации помехи (вектора ошибки) E = (e₁, e₂,..., e_n)

,

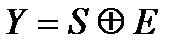где – понимается как поразрядное сложение S и E по модулю L_s. В случае двоичных последовательностей (L_s = 2) нулевой символ вектора ошибки e_i = 0 означает, что i-й символ принят правильно (y_i = s_i), а e_i = 1 указывает на ошибку в приёме (y_i ≠ s_i).

Классификацию дискретных каналов удобно вести по вектору ошибки Е. Разные модели каналов различаются распределением вероятностей вектора Е. Наиболее распространены следующие модели [2].

Канал без памяти – это канал, в котором символы e_i являются независимыми СВ. Прием каждого сигнального символа в таком канале не зависит от результата приема предыдущих символов. При наличии такой зависимости имеет место канал с памятью. Дискретный канал называется стационарным, если вероятность ошибочного приема символов не изменяется с течением времени.

В силу простоты технической реализации наибольшее применение находят каналы, сигналы в которых представляются двоичным кодом.
Такие каналы называются двоичными (бинарными) и задаются с помощью графа (рис. 14.2). Вероятности P(0/0) и P(1/1) характеризуют правильный прием символов 0 и 1 соответственно, a P(1/0) и P(0/1) – вероятности ошибок при приеме символов 0 и 1.

Симметричным двоичным называется канал, в котором вероятности ошибок при приеме 0 и 1 одинаковы, P(1/0) = P(0/1), а следовательно, равны и вероятности правильного приема символов P(0/0) = P(1/1) = 1 - p. Для симметричного стационарного канала без памяти вероятность искажения i-го символа P(e_i = 1) = p, а вероятность правильного приема P(e_i = 0) = 1 – p.

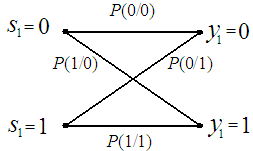
Рис. 14.2. Граф двоичного канала

Двоичный канал без памяти со стиранием отличается от рассмотренного тем, что выходной алфавит помимо 0 и 1 содержит третий символ «?» – символ стирания. Он появляется в тех случаях, когда демодулятор не может надежно опознать переданный символ. Такой канал часто используется в системах передачи информации с обратной связью, когда при приеме символа «?» производится повторение передачи. Это позволяет значительно снизить вероятность ошибочного приема за счет уменьшения скорости передачи.

Марковский канал является простейшей моделью дискретного канала с памятью. Он характеризуется вектором ошибки, символы которого образуют простую цепь Маркова [12]. Вероятность искажения символа в этом канале зависит от результата приема только предыдущего символа.

Марковская модель задается матрицей переходных вероятностей:

,

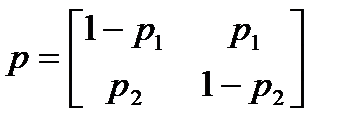где p₁ – условная вероятность принять (i + 1)-й символ ошибочно, если i-й принят правильно; 1- p₁ – условная вероятность принять (i + 1)-й символ правильно, если i-й принят правильно; p₂ – условная вероятность принять (i + 1)-й символ ошибочно, если i-й принят ошибочно; 1- p₂ – условная вероятность принять (i + 1)-й символ правильно, если i-й принят ошибочно.

Безусловная (средняя) вероятность ошибки в рассматриваемом канале должна удовлетворять уравнению:

p(x_i+1 / x_i) = p₂ ∙ p_ош(x_i) + p₁ ∙ p_прав(x_i)

или

p(x_i+1 / x_i) = p₁ / (1 + p₁ + p₂).

Данная модель имеет достоинство – простоту использования, но не всегда адекватно воспроизводит свойства реальных каналов. Большую точность позволяет получить модель Гильберта для дискретного канала с памятью. В такой модели канал может находиться в двух состояниях S₁ и S₂. В состоянии S₁ ошибок не происходит; в состоянии S₂ ошибки возникают с вероятностью p₂.

Также считаются известными вероятности перехода p(S₁ / S₂) из состояния S₁ в S₂ и вероятности перехода p(S₂ / S₁) из состояния S₂ в состояние S₁. В этом случае простую марковскую цепь образует не последовательность ошибок, а последовательность переходов:

,

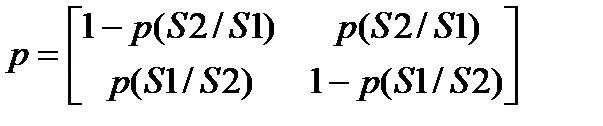При этом достаточно легко выразить безусловные вероятности нахождения канала в состояниях S₁ и S₂:

, ,

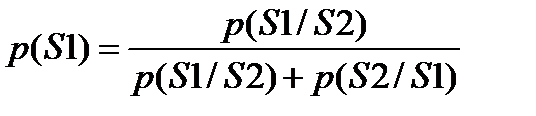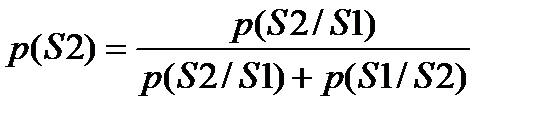Безусловная вероятность ошибки в этом случае может быть определена по формуле:

.

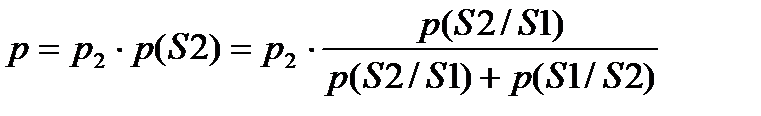Наиболее часто при использовании модели Гильберта для двоичного канала полагают p₂ = 1/2, т.е. состояние S₂ рассматривается как полный обрыв связи. Это согласуется с представлением о канале, в котором действуют коммутационные помехи.

Из других моделей симметричных двоичных каналов следует отметить канал с пакетами ошибок, который характеризуется тем, что искажающие символы (единицы) вектора ошибки группируются в пакеты. Такое группирование происходит, если в непрерывном канале, входящем в дискретный, действуют сильные замирания сигналов на время длительности нескольких символов или присутствуют импульсные помехи большой длительности. Подобные каналы задаются вероятностями искажений серий из q символов подряд.