Цепи с конечной импульсной характеристикой (КИХ-цепи)

Предположим, что импульсная характеристика некоторой цепи h[n] имеет конечную длину N, т.е. h[n] ≠ 0, 0 ≤ n ≤ N - 1. Тогда свертка (12.10) принимает вид конечной суммы

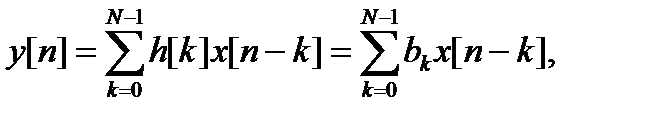
и может быть записана в виде разностного уравнения

y[n] = b₀x[n] + b₁x[n - 1] + b₂x[n - 2] + … + b_{N -1}x[n - N + 1]. (12.12)

Вычисление каждого значения выходного сигнала требует учета текущего и N - 1 предшествующих отсчетов входного сигнала и может быть выполнено цепью, структурная схема которой показана на рис. 12.3. Такие цепи называются трансверсальными, или цепями с конечной импульсной характеристикой (КИХ-цепями).

Комплексная частотная характеристика КИХ-цепи имеет вид полинома порядка N - 1 относительно e^-jω:

.

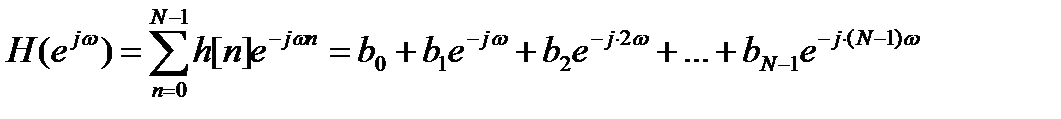Таким образом, КИХ-цепь умножает спектральную плотность входной последовательности на полином.

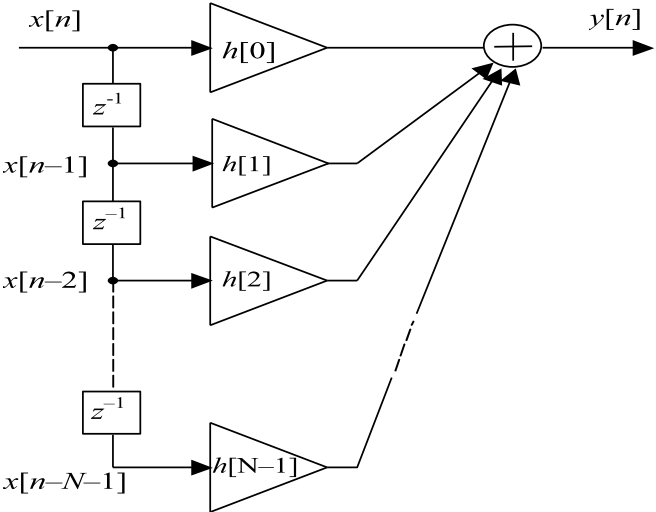
Рис. 12.3. Структура цепи с конечной импульсной характеристикой

Рекурсивные цепи

Другой важный для практики класс дискретных ЛИС-цепей составляют цепи, которые не умножают, а делят спектральную плотность входной последовательности на полином некоторого порядка M - 1 относительно e^-jω. Обозначим этот полином A(e^jω) = α₀ + α₁e^-jω + α₂e^-j∙2ω + … + α_M-1e^-j∙(M-1)ω, тогда спектральные плотности входной и выходной последовательностей связаны выражением Y(e^jω) = X(e^jω) / A(e^jω), следовательно, X(e^jω) = Y(e^jω) A(e^jω), откуда по аналогии с (12.3) можно записать

x[n] = α₀y[n] + α₁y[n - 1] + α₂y[n - 2] + … + α_M-1y[n - M + 1].

Решая это уравнение относительно выходного сигнала, получаем

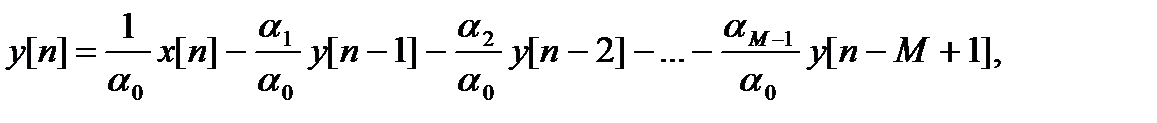
откуда, вводя обозначения b = 1/α₀, α_i = -α_i/α₀, находим окончательно разностное уравнение рекурсивной цепи

y[n] = bx[n] + α₁y[n - 1] + α₂y[n - 2] + … + α_M-1y[n - M + 1],

структура которой показана на рис. 12.4.

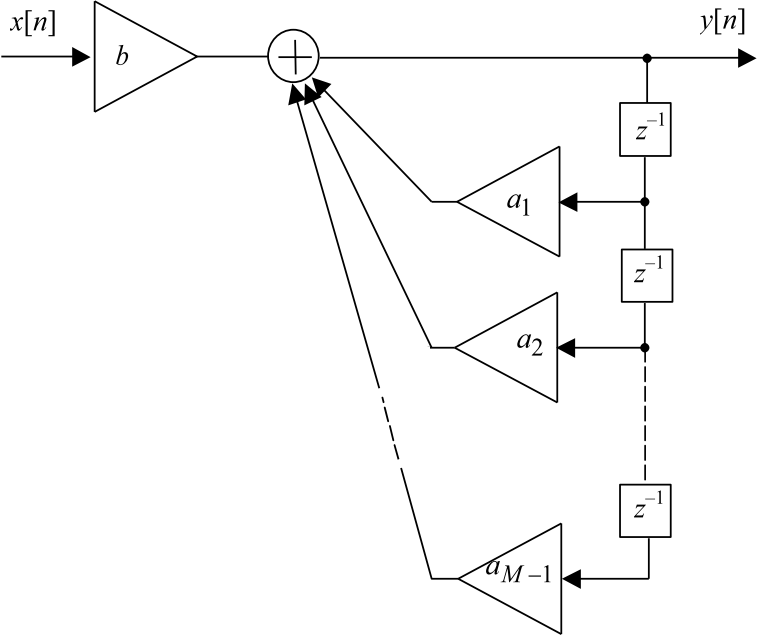
Рис. 12.4. Структура рекурсивной цепи

Устойчивость ЛИС-цепей

Обычно к ЛИС-цепям предъявляется требование устойчивости. Напомним, что линейная цепь называется устойчивой, если отклик на воздействие, ограниченное по модулю, также ограничен.

Для устойчивости ЛИС-цепи необходимо и достаточно, чтобы ее импульсная характеристика была абсолютно суммируемой, т.е. выполнялось условие [7]

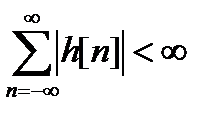. (12.13)

Очевидно, для импульсных характеристик конечной длины это условие выполняется всегда, поэтому КИХ-цепи всегда устойчивы.

Рекурсивные цепи могут быть неустойчивыми из-за наличия обратных связей. Анализ устойчивости ЛИС-цепей основан на использовании z-преобразования, которое формально может быть получено из преобразования Фурье заменой величины e^jω на комплексное переменное z:

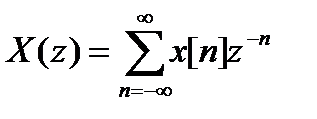. (12.14)

z-преобразование может сходиться для одних значений комплексного переменного z и расходиться для других. Множество точек комплексной z-плоскости, в которых z-преобразование сходится, называется областью сходимости. Для абсолютно суммируемой импульсной характеристики область сходимости ее z-преобразования содержит единичную окружность. Если цепь является физически реализуемой (каузальной), то она устойчива в том и только в том случае, если все полюсы ее передаточной функции

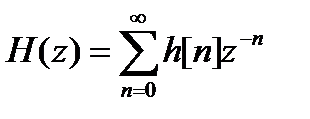
по модулю меньше единицы, т.е. находятся внутри единичной окружности.

Самый широкий класс ЛИС-цепей конечного порядка образуют цепи, структура которых может быть сведена к каскадному соединению трансверсальной и рекурсивной частей, что соответствует разностному уравнению вида

y[n] = b₀x[n] + b₁x[n - 1] + b₂x[n - 2] + … + b_N-1x[n - N + 1] +

+ α₁y[n - 1] + α₂y[n - 2] + … + α_M-1x[n - M + 1] =

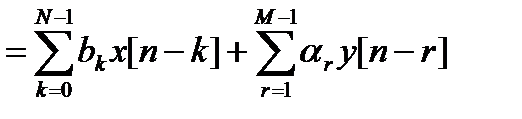, (12.15)

откуда следует выражение для КЧХ дробно-рационального вида

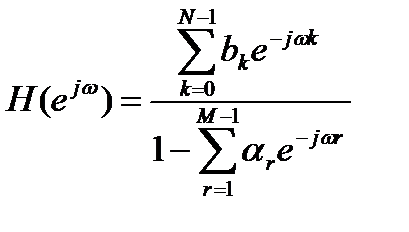. (12.16)

В общем случае ЛИС-цепь конечного порядка с КЧХ вида (12.16) имеет бесконечно длинную импульсную характеристику (БИХ), но если полином-числитель делится на знаменатель без остатка, то результатом деления оказывается полином и импульсная характеристика имеет конечную длину (таковы, например, КИХ-фильтры на основе частотной выборки, см. далее).

ЦИФРОВЫЕ ФИЛЬТРЫ

Дискретное преобразование Фурье представляет собой не только инструмент анализа, но и алгоритм ЦОС. На его основе фильтрация сигналов в частотной области может быть реализована следующим образом: для входного сигнала вычисляется ДПФ, полученные спектральные отсчеты умножаются на КЧХ фильтра, а результат умножения подвергается обратному ДПФ. Этот метод фильтрации более экономичный, чем вычисление свертки входного сигнала с импульсной характеристикой фильтра, благодаря существованию очень эффективных (быстрых) алгоритмов, которые получили название быстрого преобразования Фурье (БПФ).

Основное назначение дискретных ЛИС-цепей заключается в фильтрации дискретных сигналов, т.е. в избирательном воздействии на амплитуды и начальные фазы гармонических составляющих различных частот. Это фактически означает, что любая ЛИС-цепь представляет собой фильтр. Однако интерес представляет построение фильтров с заданными частотно-избирательными и фазовыми свойствами. Построить (синтезировать) фильтр – значит найти его разностное уравнение (т.е. алгоритм вычисления выходного сигнала по известному входному) и/или структурную схему.

Таким образом, под синтезом цифрового фильтра (ЦФ) обычно понимается построение дискретной ЛИС-цепи с КЧХ заданной формы. При решении задачи синтеза обычно не делают различия между дискретными и цифровым цепями, хотя, строго говоря, дискретная ЛИС-цепь становится цифровой в результате квантования коэффициентов ее разностного уравнения.

Ранее было показано, что ЛИС-цепь конечного порядка имеет в общем случае КЧХ дробно-рационального вида (12.7), поэтому, очевидно, задача синтеза ЦФ сводится к аппроксимации желаемой КЧХ функцией дробно-рационального вида, так как, зная эту функцию, легко составить структурную схему цепи или записать разностное уравнение вида (12.6). Указанная аппроксимация сравнительно легко выполняется для КИХ-цепей, когда дробнорациональная функция вырождается в полином, и представляет собой непростую задачу для общего случая. Поэтому методы синтеза ЦФ с конечными и бесконечными импульсными характеристиками различаются.

Методы синтеза КИХ-фильтров

Фильтры с конечной импульсной характеристикой имеют перед БИХ-фильтрами ряд преимуществ. Во-первых, КИХ-фильтры всегда устойчивы. Во-вторых, только КИХ-фильтр может иметь строго линейную фазочастотную характеристику [7] (фильтр с линейной ФЧХ не искажает форму сигнала, если его спектр лежит в полосе частот, где амплитудно-частотная характеристика постоянна; при этом сигнал лишь задерживается на время, пропорциональное крутизне ФЧХ). Наконец, для КИХ-фильтров наиболее просто решается задача аппроксимации КЧХ желаемого вида реализуемой функцией (тригонометрическим полиномом). Однако КИХ-фильтры имеют существенный недостаток по сравнению с БИХ-фильтрами: для обеспечения сравнимых частотно-избирательных свойств, в частности крутизны АЧХ в переходной полосе частот, требуется КИХ-фильтр в десятки раз более высокого порядка, чем БИХ-фильтр. На практике в зависимости от конкретных обстоятельств применяются фильтры обоих типов. Ниже вкратце рассматриваются методы синтеза КИХ-фильтров.

Метод взвешивания (метод функций окна)

КЧХ трансверсального дискретного фильтра представляет собой тригонометрический полином, т.е. функцию вида

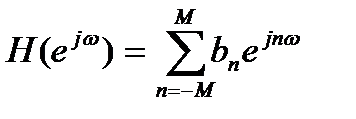. (13.1)

Здесь не предполагается каузальность фильтра; если каузальность необходима, ее легко можно обеспечить умножением (13.1) на фазовый множитель e^-jMω. Если желаемая КЧХ имеет вид H_ж(e^jω), то синтез КИХ-фильтра состоит в нахождении тригонометрического полинома, близкого в каком-то смысле к H_ж(e^jω). Обычно в качестве критерия близости выбирается среднеквадратическая ошибка аппроксимации

,

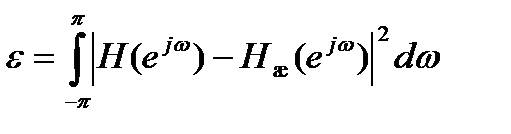тогда наилучшая аппроксимация обеспечивается, если коэффициентами полинома (13.1) являются коэффициенты разложения желаемой КЧХ в ряд Фурье

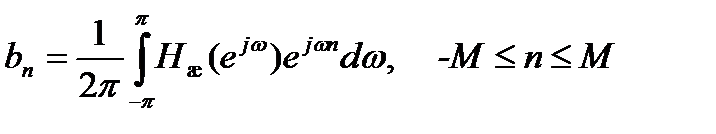. (13.2)

Эти коэффициенты представляют собой отсчеты импульсной характеристики КИХ-фильтра, в общем случае некаузального. После соответствующей задержки получается импульсная характеристика каузального фильтра h[n] = b_n-M, 0 ≤ n ≤ N – 1, где N = 2M + 1. Поскольку всякая ЛИС-цепь однозначно определяется своей импульсной характеристикой, на этом синтез КИХ-фильтра можно было бы считать законченным. Однако если желаемая КЧХ разрывна (например, как часто бывает на практике, требуется АЧХ прямоугольной формы), получаемая КЧХ, как сумма усеченного ряда Фурье (13.1), содержит гиббсовские осцилляции. Поэтому применяют дополнительное умножение импульсной характеристики на весовую последовательность («окно») подходящей формы.

Причина явления Гиббса заключается в слишком медленном убывании коэффициентов Фурье-разложения разрывной функции, поэтому все применяемые окна убывают от середины к краям [7]. Для достижения приемлемых избирательных свойств длина импульсной характеристики, определяющая объем вычислений, на практике составляет обычно несколько сотен.

Кроме метода взвешивания, иногда применяют другой способ борьбы с гиббсовскими осцилляциями. На этапе формулирования требований к фильтру вводят переходную полосу, в которой задают закон непрерывного изменения АЧХ (например, линейный закон) [7]. Тогда ряд Фурье сходится равномерно и явление Гиббса отсутствует. Это не означает, что исчезает неравномерность АЧХ, просто осцилляции теперь убывают по амплитуде с увеличением порядка фильтра.

Следует также упомянуть машинные методы синтеза КИХ-фильтров на основе численной оптимизации. При этом подбором коэффициентов КИХ-фильтра минимизируется взвешенная среднеквадратическая ошибка

,

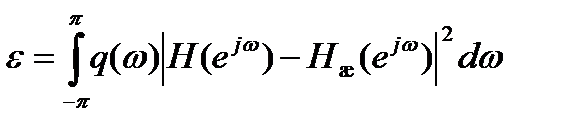где q(ω) – весовая функция, позволяющая управлять относительной значимостью ошибок на разных участках частотной оси, или максимальная взвешенная погрешность

.

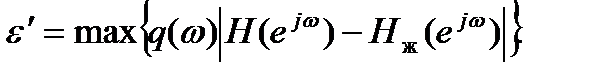Эти методы позволяют получить меньшие погрешности аппроксимации по сравнению с описанным выше методом оконного взвешивания, но их анализ значительно сложнее [7].

Метод частотной выборки

Метод синтеза фильтров с конечной импульсной характеристикой, получивший название метода частотной выборки, основан на задании значений желаемой КЧХ в точках, расположенных равномерно на единичной-окружности и соответствующих точкам частотной оси (отсюда название метода) и аппроксимации КЧХ интерполяционным полиномом Лагранжа [7]. Этот метод приводит к построению структуры, содержащей трансверсальную и рекурсивную части, которой, тем не менее, соответствует конечная импульсная характеристика. Благодаря наличию рекурсии такие фильтры при реализации требуют меньшего числа операций по сравнению с рассмотренными выше КИХ-фильтрами и оказываются предпочтительными.

Метод быстрой свертки

Фильтрация сигналов может быть выполнена в частотной области путем вычисления спектральной плотности входного сигнала, умножения ее на КЧХ фильтра и выполнения обратного преобразования Фурье (на практике для входного сигнала, который представляет собой реализацию случайного процесса, можно вычислить только дискретное преобразование Фурье). Этот на первый взгляд сложный способ нахождения выходного сигнала оказывается на практике более эффективным в вычислительном отношении, чем прямое вычисление свертки, благодаря существованию алгоритмов быстрого преобразования Фурье. Метод КИХ-фильтрации на основе БПФ получил название метода быстрой свертки.

При его реализации необходимо учитывать следующие два обстоятельства. Первое состоит в том, что дискретное преобразование Фурье обладает двойственностью – оно соответствует как последовательностям конечной длины, так и периодическим последовательностям. По этой причине перемножение коэффициентов ДПФ двух последовательностей (входного сигнала и импульсной характеристики) соответствует не обычной (апериодической), а так называемой циклической (круговой) свертке.

Убедимся, что это действительно так.

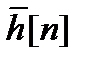Пусть и – периодические последовательности с периодом N. Их циклическая свертка определяется выражением

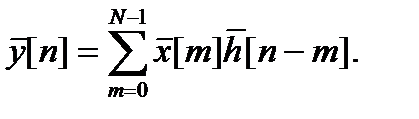
ДПФ результирующей последовательности

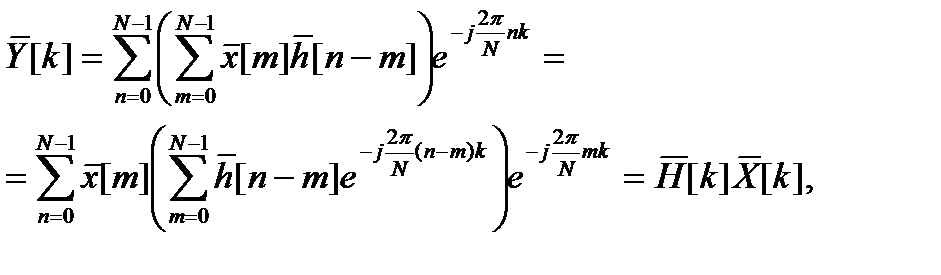(13.3)

,

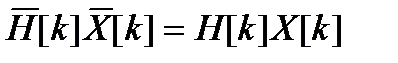где 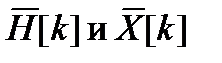находятся как ДПФ N-периодических последовательносте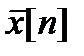й и 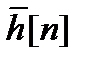, а H[k] и X[k] – как ДПФ их конечных фрагментов длины.

При выводе (13.3) учтен тот факт, что сумма в круглых скобках во второй строке равна 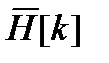независимо от m в силу периодичности суммируемых членов: при различных m суммируются одни и те же N слагаемых в разном порядке. Таким образом, видно, что циклическая свертка (или свертка периодических последовательностей) соответствует поточечному произведению ДПФ-спектров последовательностей. При фильтрации же должна выполняться обычная апериодическая свертка, определяемая выражением (13.2).

Преодолеть эту трудность можно следующим образом. Преобразование Фурье последовательности длины N дает полином (относительно e^-jω) степени N - 1. Полагая, что x[n] и h[n] – последовательности длины N, видим, что произведение их фурье-образов есть полином степени 2(N – 1). Но при поточечном перемножении ДПФ-спектров, имеющих по N отсчетов, получается всего N результирующих отсчетов, что соответствует полиному всего лишь (N – 1)-й степени. Единственный способ получения правильного результата умножения двух полиномов состоит в том, чтобы точек вычисления ДПФ «хватило» для представления результата. Иначе говоря, если используется N-точечное ДПФ, то степень результирующего полинома должна быть не выше (N – 1). Это, в свою очередь, означает, что сумма длин последовательностей x[n] и h[n] (обозначим их M и L) должна удовлетворять очевидному соотношению M - 1 + L - 1 ≤ N - 1 (или M + L - 1 ≤ N). Для того чтобы можно было для последовательности x[n] длины M < N получить N отсчетов ДПФ, следует перед вычислением ДПФ последовательность x[n] дополнить N - M нулевыми отсчетами (и то же проделать с другой последовательностью). Тогда результат их циклической свертки, полученный применением БПФ, совпадает с результатом апериодической свертки.

Второе обстоятельство, которое должно учитываться при реализации КИХ-фильтрации методом быстрой свертки, относится к фильтрации последовательностей большой (в частности, бесконечной) длины. Если длина входной последовательности велика (сотни тысяч отсчетов и более), что типично для обработки сигналов, применяемых в радиотехнике и связи, то необходимое основание БПФ (число вычисляемых отсчетов) оказывается слишком большим. Это влечет за собой высокие требования к объему оперативной памяти вычислителя БПФ, а также приводит к большой задержке результирующего сигнала (результат может быть получен не ранее чем поступит последний отсчет входной последовательности плюс время, необходимое для вычисления прямого БПФ, умножения и обратного БПФ). Для того чтобы снизить требования к памяти и уменьшить задержку, применяют секционирование свертки [7].

Пусть h[n] – импульсная характеристика фильтра, имеющая длину M, а x[n] – сигнальная последовательность бесконечной длины. Представим x[n] в виде

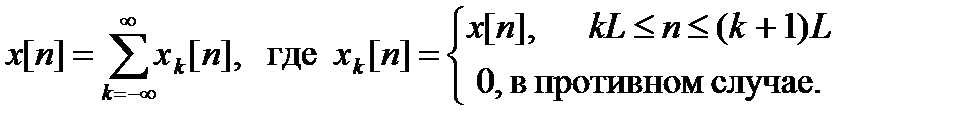
Нетрудно видеть, что таким образом входная последовательность разбивается (секционируется) на совокупность неперекрывающихся примыкающих друг к другу сегментов длиной L отсчетов каждый.

В силу билинейности свертки (линейности по каждому из операндов)

.

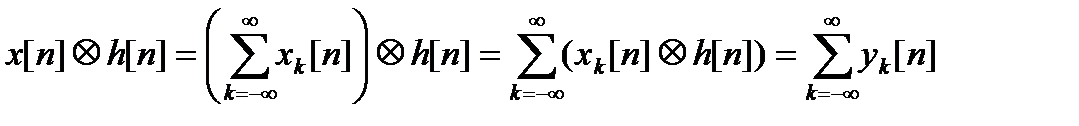Как видно из полученного выражения, свертка последовательности бесконечной длины с конечной импульсной характеристикой может быть точно заменена бесконечной суммой сверток сегментов фиксированной длины с этой же импульсной характеристикой. Каждая частичная свертка требует для своего вычисления (L + M – 1)-точечного БПФ. Поскольку L выбирается произвольно, секционирование позволяет реализовать КИХ-фильтрацию длинных (потенциально – бесконечно длинных) последовательностей; при этом результат y_k[n] фильтрации сегмента x_k[n] появляется с задержкой, определяемой временем прямого и обратного БПФ и умножения, но эта задержка теперь отсчитывается от момента окончания сегмента, а не всей последовательности.

Результат каждой частичной свертки имеет длину (L + M - 1), а следуют секции с относительным сдвигом L. Таким образом, результаты частичных сверток y_k[n] суммируются с перекрытием носителей kL ≤ n ≤ (k + 1) L + M - 1. Этот метод секционирования свертки известен как метод перекрытия с суммированием (overlap-add method) [7].

Альтернативный метод перекрытия с накоплением (overlap-save method) заключается в том, что перекрываются сегменты входной последовательности. Последовательность x[n] разбивается на секции x_k[n] длиной (L + M – 1), причем последние (M - 1) отсчетов каждой секции перекрываются с таким же количеством первых отсчетов следующей секции (M – по-прежнему длина импульсной характеристики, L выбирается произвольно). Каждая секция подвергается БПФ с основанием (L + M – 1). Импульсная характеристика длиной M дополняется нулями до основания БПФ. Результат фильтрации (циклической свертки) содержит всего (L + M – 1) отсчетов, из которых последние (M - 1) отсчетов – «ошибочные», не совпадающие с результатом апериодической свертки, а остальные L отсчетов являются «правильными». Суммируются результаты циклических частичных сверток после отбрасывания «ошибочных» отсчетов, т. е. секции выходной последовательности длиной L следуют друг за другом без перекрытия.