Расчет на прочность и жесткость при деформации растяжения
С помощью математического пакета ANSYS Mechanical была создана модель стержня, закрепленного с одной стороны и подверженного силам растяжения с другой.
Рис.2.1. Схема деформирования
стержня (Beam188)
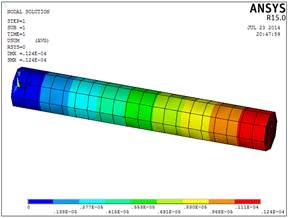
Рис.2.2.Абсолютное удлинение
стержня (м)(Beam188)
Внутренние продольные силы и нормальные напряжения распределяются равномерно по всей длине стержня.
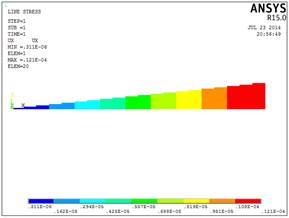
Рис.2.3. Эпюра абсолютных деформаций (м)
Как показано на рисунке 2.3 абсолютные деформации возрастают от места закрепления к свободному концу стержня.
Мы сравнили полученные аналитическое решение и компьютерные расчеты. Графическое представление результатов показано на рисунке 2.4.
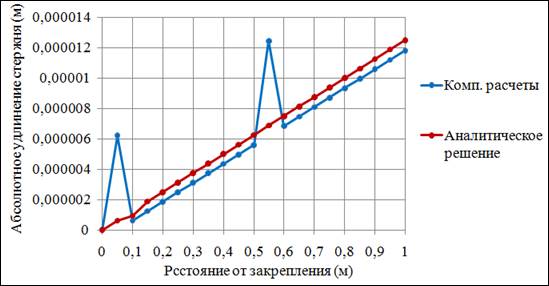
Рис.2.4. График зависимости абсолютного удлинения
стержня от расположения точки
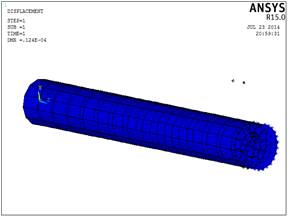
Рис.2.5. Схема деформирования
стержня(Solid186)
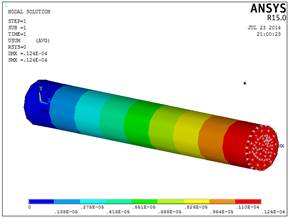
Рис.2.6. Абсолютное удлинение
стержня (м)(Solid186)
Расчеты, полученные при нагрузке стержня, имеющего тип элемента Solid186, сравнили с аналитическим решением по максимальному значению. Результаты совпадают до шести знаков после запятой.
Расчет на прочность и жесткость при деформации кручения
Для расчета напряженно-деформированного состояния стержня при кручении была создана модель стержневой конструкции, имеющей жесткое закрепление с одной стороны. С другой стороны стержня задается крутящий момент вдоль оси OZ.
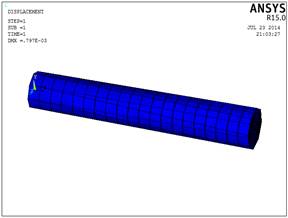
Рис.2.7. Схема деформирования
стержня(Beam188)
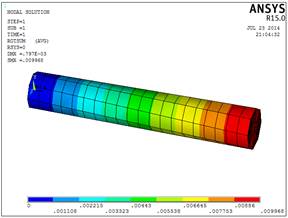
Рис.2.8.Распределение углов закручивания (рад)(Beam188)
Внутренние крутящие моменты распределены равномерно по всей длине стержня. Значения углов закручивания стержня увеличиваются в направлении от места закрепления к свободному концу конструкции, как это показано на рисунке 2.9.
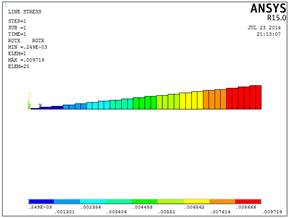
Рис.2.9. Эпюра углов
закручивания (рад)
Сравнение результатов, полученных аналитическим путем и с помощью компьютерных расчетов, приведено на рисунке 2.10.
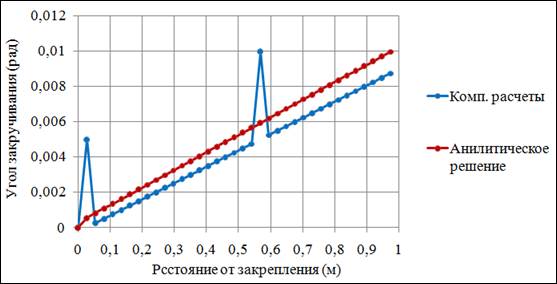
Рис.2.10. График зависимости угла закручивания
стержня от расположения точки
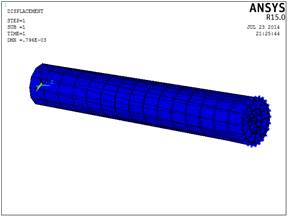
Рис.2.11. Схема деформирования
стержня (Solid186)
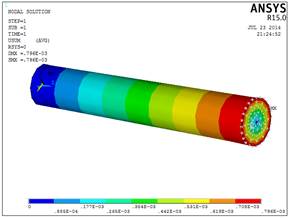
Рис.2.12. Вектор перемещения (м) (Solid186)
Расчеты, полученные при нагрузке стержня, имеющего тип элемента Solid186, также сравнили с аналитическим решением по максимальному значению. Результаты совпадают до шести знаков после запятой.
Расчет на прочность и жесткость при чистом изгибе
Для расчета напряжения и деформации при чистом изгибе была построена модель стержня постоянного сечения, шарнирно закрепленного с двух сторон и подверженного нагрузке, приходящейся на середину конструкции. Визуальное представление полученных данных приведено ниже.
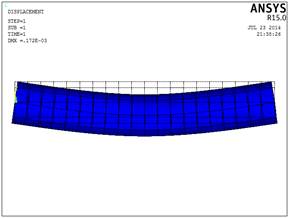
Рис.2.13. Схема деформирования
стержня(Beam188)
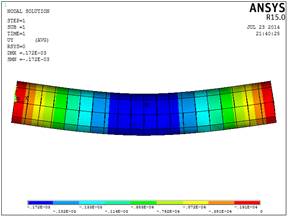
Рис.2.14. Прогибыпо оси OY(м)
(Beam188)
По приведенным выше рисункам видно, что наибольшие прогибы наблюдаются непосредственно в месте приложения силы.
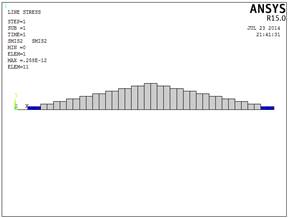
Рис.2.15. Эпюра внутренних
поперечных сил (Н)
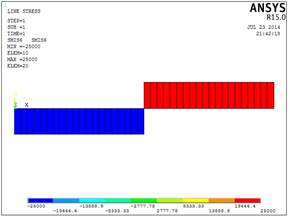
Рис.2.16. Эпюра изгибающих
моментов (Н×м)
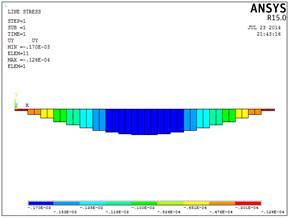
Рис.2.17. Эпюра прогибов (м)
