Показательная функция (20 ч.)

Процессы показательного роста и показательного убывания. Показательная функция. Свойства показательной функции. Решение задач на применение свойств показательной функции.

Показательные уравнения. Решение показательных уравнений на основании свойств показательной функции. Решение показательных уравнений с помощью разложения на множители, заменой переменной, решение однородных показательных уравнений.

Решение систем, содержащих показательные уравнения.

Решение показательных неравенств и систем, содержащих показательные неравенства. Решение нестандартных уравнений и неравенств, задач интегрированного характера.

Основные Требования

к результатам учебной деятельности учащихся

Учащийся д о л ж е н:

знать:

определение и свойства показательной функции; методы решения показательных уравнений и неравенств;

иметь представлениео показательной функции как математической модели, которая находит широкое применение при изучении процессов и явлений окружающего мира (радиоактивный распад вещества, рост колонии бактерий);

уметь:

строить графики показательной функции с различными основаниями; применять свойства и графики показательной функции с различными основаниями для сравнения значений показательной функции, для определения множества значений, наибольшего и наименьшего значений выражений;

решать показательные уравнения на основании свойств показательной функции, с помощью разложения на множители, заменой переменной, решать однородные показательные уравнения;

решать показательные неравенства на основании свойств показательной функции с помощью разложения на множители, заменой переменной, решать однородные показательные неравенства;

решать системы показательных уравнений;

решать системы показательных неравенств;

использовать приемы поиска и решения нестандартных уравнений и неравенств.

применять полученные знания при решении задач практической направленности.

Логарифмическая функция (35 ч.)

Свойства логарифмов: логарифм произведения, частного, степени. Формула перехода от логарифма с одним основаниемк логарифму с другим основанием. Десятичный логарифм.

Логарифмическая функция. Свойства логарифмической функции. Решение задач на применение свойств логарифмической функции.

Решение логарифмических уравнений на основании свойств логарифмической функции и свойств логарифмов. Решение логарифмических уравнений заменой переменных.

Решение логарифмических неравенств.

Решение систем логарифмических уравнений и логарифмических неравенств. Решение нестандартных уравнений и неравенств, задач интегрированного характера.

Основные Требования

к результатам учебной деятельности учащихся

Учащийся д о л ж е н:

знать:

свойства логарифмов: логарифм произведения, частного, степени; формулу перехода от логарифма с одним основанием к логарифму с другим основанием; определение десятичного логарифма; определение и свойства логарифмической функции, как функции, обратной показательной; методы решения логарифмических уравнений и неравенств;

уметь:

строить графики логарифмической функции с различными основаниями;

применять свойства и графики логарифмической функции с различными основаниями для сравнения значений логарифмической функции, для нахождения области определения и множества значений, наибольшего и наименьшего значений выражений;

решать логарифмические уравнения на основании свойств логарифмической функции, с помощью разложения на множители, заменой переменной, решать системы логарифмических уравнений;

решать логарифмические неравенства и их системы;

использовать приемы поиска и решения нестандартных уравнений и неравенств;

применять полученные знания при решении задач практической направленности.

Производная (26 ч.)

Производная, физический смысл производной, геометрический смысл производной. Производные функций:

y = c, y = ax + b, y = ax² + bx + c,

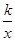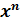y = ,y = , n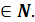

Правила нахождения производных: (cf)¢ = cf¢, (f + g)¢ = f ¢ + g¢, (fg)¢ = f ¢g + fg¢, = .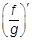

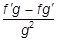Связь между знаком производной функции и её возрастанием или убыванием.

Уравнение касательной к графику функции.

Нахождение наибольшего и наименьшего значений функции на промежутке.

Применение производной к исследованию функций, решению уравнений и неравенств.

Основные Требования

к результатам учебной деятельности учащихся

Учащийся д о л ж е н:

знать:

физический и геометрический смысл производной; правила нахождения производной суммы, разности, произведения, частного функций; связь между возрастанием (убыванием) функции и знаком ее производной;

уметь:

находить производную функции по правилам нахождения производных;

находить значения производной в точке;

определять промежутки монотонности, точки экстремума, экстремумы функции;

решать задачи на нахождение наибольшего и наименьшего значений функции на промежутке;

составлять уравнение касательной к графику функции;

уметь использовать производную при исследовании функций и построении графиков;

применять полученные знания при решении задач практической направленности.