Техническое обслуживание систем по состоянию

Техническое обслуживание систем по состоянию с периодическим контролем.

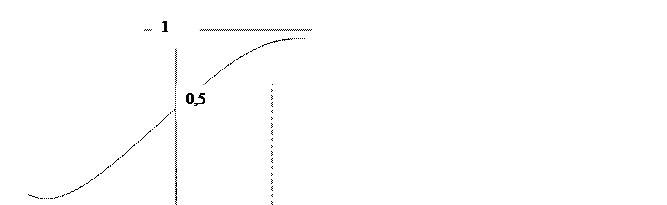
При решении задачи будем предполагать, что техническое состояние изделия определяется численными значениями специально выбранных контролируе­мых параметров. Пусть далее η(t)—монотонная случайная функция времени t, соответствующая контролируемому параметру изделия, η**—предельно допустимое значение параметра, пересечение которого реализациями случайного процесса приводит к отказам изделия, а η* — наименьшее предотказовое значение параметра, такое, что интер­вал Δη = η** - η* определяет упреждающий допуск (рис.5.4). Область 0, η* изменения случайной функции будем называть исправ­ным состоянием изделия (состояние 1), область (η*, η**) изменения η(t) будем называть состоянием профилактических замен (состояние 2), а область( η **,∞)— неработоспособным (состояние 3).

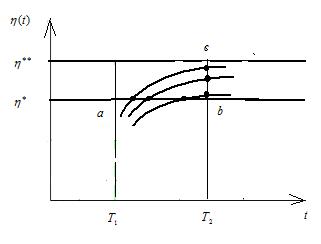
Рис.5.4 Связь периодичности проверок (τ = Т₂-Т₁) с упреждающим допуском

Δη = η **- η *на диагностиче­ский параметр (модель экранов).

Предполагается, что при замене устанавливается новое изделие или отремонтированное, причем последнее по своему техническому состоянию эквивалентно новому. В дальнейшем рассмотрим вопросы оценки момента первой проверки Т₁ и упреждающего допуска Δη

Оценка момента первой проверки.

Очевидно надежность системы равна

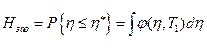
или

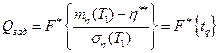
Отсюда

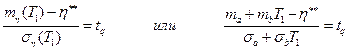
Таким образом

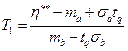
Оценка упреждающего допуска.

Условие безотказности системы на интервале обслуживания определяется равенством

где 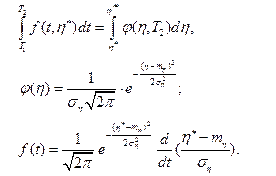(5.15)

Выполнение условия (5.15) обеспечивает такое расположение 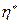, при котором все траектории процесса, прошедшие через горизонтальный участок (a , b ) попадают на вертикальный участок ( b , c )(см. рис. 5.4 ).

В дальнейшем оценим первый интеграл соотношения (1)

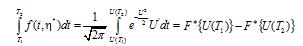
Производя линеаризацию F^*{U} в окрестности нуля (см. рис.5.5), приближенно получим

F^*(U)

U(T₂) 0 U(T₁) U

Рис.5.5 Функция нормированного нормального распределения

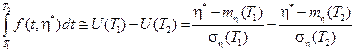
Соответственно для второго интеграла найдем

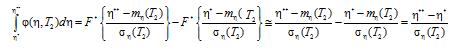
Приравнивая интегралы между собой, получим

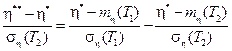
После преобразований имеем

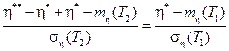
Отсюда

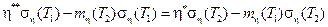
Таким образом

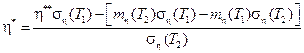(5.16)

В случае линейной зависимости

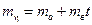
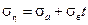
выражение в квадратных скобках в соотношении (5.16) будет равно

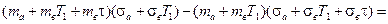
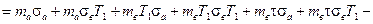
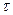
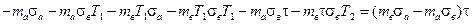
Таким образом, выражение для η^* примет вид

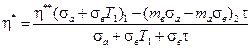(5.17)

Соответственно

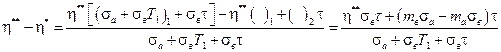(5.18)

Соотношения (5.17) и (5.18) позволяют оценивать периодичность обслуживания 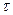в зависимости от величины упреждающего допуска .

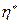Техническое обслуживание систем по состоянию с непрерывным контролем.

Перспективным направлением организации технического обслуживания является эксплуатация систем по состоянию, которая предполагает периодический контроль и измерение параметров, определяющих техническое состояние изделий. При этом решение о замене или восстановлении работоспособности изделия принимается тогда, когда значение параметров работоспособности достигают критического уровня соответствующего отказу.

Для анализа предлагаемого подхода проанализируем возможные реализации монотонно возрастающего случайного процесса. Очевидно, достижение допустимого уровня приводит к отказу устройства. Следовательно останавливать наблюдение и проводить замену необходимо до достижения критического уровня. В дальнейшем решим задачу отыскания оптимального момента замены системы по информации о поведении конкретной реализации процесса. Допустим, что после проведения «i» наблюдений известно, что изделие находится в работоспособном состоянии. Для решения вопроса о целесообразности его замены нужно оценить работоспособность системы на (i + 1) – ом шаге ее функционирования.

Таким образом возникает задача прогнозирования поведения случайного процесса y(t) на (i +1) – ом шаге по результатам измерений в предшествующие моменты времени. Существуют различные методы прогнозирования случайных процессов .

В дальнейшем остановимся на методе наименьших квадратов, нашедшем широкое применение в инженерной практике.

При решении задачи будем предполагать, что случайная функция может быть представлена в виде

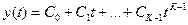
или в матричной форме

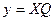(5.19)

где 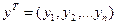- вектор значений функции;

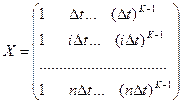- матрица известных координат;

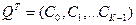- вектор неизвестных параметров;

n – число измерений;

K – число неизвестных параметров.

С учетом случайных воздействий уравнение (5.19) примет вид

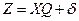
где 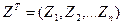- вектор измерений;

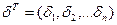- вектор случайных воздействий.

Согласно методу наименьших квадратов оценки неизвестных параметров 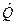удовлетворяют соотношению

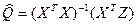
Точность оценок определяется дисперсионной матрицей

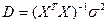
где 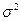- дисперсия случайных воздействий .

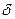При отсутствии априорной информации о статистических свойствах случайных воздействий, неизвестную дисперсию 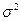можно оценить по соотношению

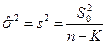
где 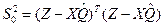- остаточная сумма квадратов.

Очевидно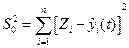

Полученные результаты могут быть применены для получения доверительного интервала, содержащего последующее (n+1) – ое значение 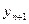величины y. Если 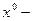заданные значения регрессоров, соответствующие значению 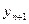, то несмещенная оценка математического ожидания 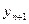будет равна

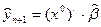, где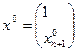

Поскольку 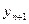имеет дисперсию 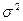, то дисперсия 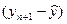увеличивается на эту величину, то-есть

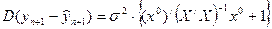
Подставляя 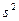вместо 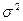приходим к статистике Стьюдента

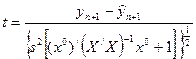
Очевидно верхняя граница доверительного интервала для значения 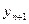удовлетворяет условию

,

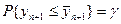где 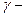уровень доверительной вероятности.

Вычитая из обоих частей неравенства значение 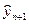и деля на среднее квадратическое отклонение разности 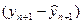, получим

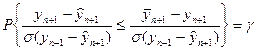
Разность 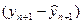подчиняется нормальному распределению с нулевым математическим ожиданием. Поэтому левая часть неравенства подчиняется распределению Стьюдента. Таким образом соотношение примет вид

,

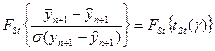где 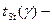аргумент функции распределения Стьюдента, соответствующий уровню доверительной вероятности .

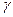Приравнивая аргументы , входящие в левую и правую часть равенства, получим

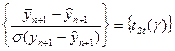
Разрешая соотношение относительно искомого параметра 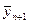, окончательно получим

,

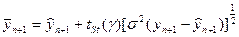где .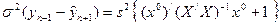

Параметр t оценивается по таблице квантилей распределения Стьюдента (см. табл. 5.1 ) . Для заданного 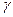величина 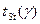определялась для числа степеней свободы f= n-2, где n –текущий объем выборки

Квантили распределения Стьюдента Таблица5.1

f		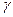f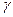
0,8	0,9	0,95	0,98	0,8	0,9	0,95	0,98
	3,07	6,31	12,70	31,82		1,345	1,761	2,145	2,624
	1,88	2,92	4,30	6,69		1,341	1,753	2,131	2,602
	1,63	2,35	3.18	4,54		1,337	1,746	2,120	2,583
	1,53	2,13	2,77	3,74		1,333	1,740	2,110	2,567
	1,47	2,01	2,57	3,36		1,330	1,734	2,101	2,552
	1,44	1,94	2,44	3,14		1,328	1,729	2,093	2,539
	1,41	1,89	2,36	2,99		1,325	1,725	2,086	2,528
	1,39	1,86	2,30	2,89		1,323	1,721	2,080	2,518
	1,38	1,83	2,26	2,82		1,321	1,717	2,074	2,508
	1,37	1,81	2,22	2,76		1,319	1,714	2,069	2,500
	1,36	1,79	2,20	2,71		1,318	1,711	2,064	2,492
	1,356	1,78	2,17	2,68		1,316	1,708	2,059	2,485
	1,35	1,77	2,16	2,65		1,315	1,706	2,056	2,479

Лекция №17