Методы прогнозирования и обеспечения надежности КА
МАИ
А.А. Золотов,
Методы прогнозирования и обеспечения надежности КА
Методическое пособие по курсу
« Надежность и отработка КА »
( специальность160400)
Утверждено на заседании каф.601
-------------------------------------------------------
Оглавление
Введение
Теории надежности.
1.1 Основные понятия и термины.
1.2 Формальная теория надежности.
1.3 Общая теория надежности.
Обеспечение надежности на этапе проектной разработки.
2.1 Расчет надежности элемента системы.
2.2 Расчет надежности систем с последовательным
соединением элементов.
2.3 Расчет надежности резервированных систем.
2.4 Расчет надежности систем произвольной структуры.
2.5 Нормирование надежности систем .
Обеспечение надежности на этапе экспериментальной отработки.
3.1 Оценка надежности по результатам испытаний.
3.2 Планирование автономной отработки элементов систем.
3.3 Согласование результатов испытаний на различных этапах ЭО.
Обеспечение надежности на этапе производства.
4.1 Оценка стабильности технологического процесса.
4.2 Статистический приемочный контроль продукции ( метод Неймана-
-Пирсона ).
4.3 Статистический приемочный контроль продукции ( метод
последовательного анализа ).
Обеспечение надежности на этапе эксплуатации.
5.1 Стратегия аварийных замен.
5.2 Стратегия технического обслуживания по гарантированному ресурсу.
5.3 Техническое обслуживание систем по состоянию.
5.4Стратегия минимального аварийного восстановления.
5.5 Стратегия строго-периодического восстановления.
5.6 Стратегия восстановления с зонами бездействия.
Литература.
Приложение.
Введение
Современный этап освоения космического пространства характеризуется ростом масштабности научных и народно-хозяйственных задач, решаемых с помощью различных космических аппаратов.
Реализация перспективных космических программ требует дальнейшего совершенствования методических и организационно-технических основ обеспечения эффективности и надежности ракетно-космических систем(РКС).Решение задачи обеспечения высоких уровней надежности РКС связано с большими затратами материальных средств на их экспериментальную отработку(ЭО) и эксплуатацию. Снижение затрат на ЭО достигается путем повышения информативности испытаний, использования ускоренных испытаний, обеспечения высоких уровней имитации при проведении испытаний, а также введением различных видов избыточности.
Очевидно высокие уровни надежности на начальном этапе эксплуатации еще не гарантируют безотказности функционирования объектов РКС , так как при их эксплуатации происходит снижение работоспособности, связанное с процессами износа, коррозии, усталости и др. Это обуславливает необходимость технического обслуживания (ТО) объектов РКС с целью предупреждения неисправностей и устранения возникающих отказов. При решении этой задачи определяющее значение приобретают вопросы прогнозирования технического состояния РКС. Их решение позволяет обосновывать оптимальные стратегии технического обслуживания , обеспечивающие удовлетворение заданных требований к надежности объектов РКС в течении всего периода их эксплуатации при минимальных затратах средств.
В дальнейшем, в предлагаемой пособии, излагаются методы решения рассмотренных выше задач.
Лекция №1
Теории надежности.
1.1. Основные понятия и термины.
Надежностью объекта называется свойство объекта выполнять заданные функции, сохранять во времени значения установленных эксплуатационных показателей в заданных приделах, соответствующих заданным режимам и условиям использования, технического обслуживания, ремонтов, хранения и транспортирования.
Надежность является комплексным свойством, которое в зависимости от назначения объекта и условий его эксплуатации может включать безотказность, долговечность, ремонтопригодность и сохраняемость в отдельности или определенное сочетание этих свойств, как для объекта, так и для его частей.
Безотказность – свойство объекта сохранять работоспособность непрерывно в течение некоторого времени или некоторой наработки. Свойство безотказности проявляется в зависимости от назначения объекта, как в режиме его работы, так и в режиме ожидания работы.
Долговечность – свойство объекта сохранять работоспособность до перехода в предельное состояние с возможными перерывами для технического обслуживания и ремонтов.В отличие от свойства безотказности долговечность характеризует продолжительность работы объекта по суммарной наработке, перерываемой периодами для восстановления его работоспособности в плановых и неплановых ремонтах и техническом обслуживании.
Ремонтопригодность – свойство объекта, заключающегося в его приспособленности к предупреждению и обнаружению отказов и повреждений, к восстановлению работоспособности и исправности путем проведения технического обслуживания и ремонта. Свойство ремонтопригодности количественно характеризует компоновочные решение МС (машин, агрегатов, сборочных единиц и деталей), а также их доступность и легкосъемность.
Сохраняемость – свойство объекта непрерывно сохранять исправное и (или) Работоспособное состояние после режима ожидания, хранения и (или) транспортирования. Свойство сохраняемости характеризует способность объекта противостоять отрицательному влиянию факторов длительного его хранения или транспортирования и обеспечивать его применение после режима ожидания с заданными показателями функционирования с сохранением показателей безотказности и долговечности как объекта в целом, так и его элементов.
Проведенный анализ показывает, что конкретный уровень носителей должен назначаться с учетом особенностей его целевого назначения, а так же возможных последствий отказа ЛА.Для большинства существующих носителей уровни надежности не достигают значения 0.99.Для иллюстрации в табл. 1.1 представлены статистические данные по результатам пуска зарубежных ракет-носителей.
Таблица 1.1.
| ЛА | Число успешных пусков | Общее число пусков | НЛА |
| Титан 3С/34 | 0,83 | ||
| Атлас Центавр | 0,85 | ||
| Дельта | 0,93 | ||
| Скаут | 0,87 | ||
| Ариан | 0,79 | ||
| Сатурн – 1 | |||
| Сатурн – 1, В | |||
| Сатурн – V | 0,92 | ||
| Тор-Анджена | 0,92 | ||
| Тор-Дельта | 0,95 | ||
| Титан-Центавр | 0,88 | ||
| Атлас-Анджена | 0,75 |
Уровни надежности, приведенные в последнем столбце таблицы, характеризуют точечную оценку надежности, рассчитанную по соотношению
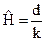 ,
,
где k - общее число испытаний; d - число безотказных испытаний.
При ограниченных объемах испытаний эта оценка не дает гарантированный результат. В частности при проведении безотказных испытаний ( k = d ) точечная оценка будет равна 1 для всех К, в том числе и для К = 1. Очевидно, доверие к этой оценке мало. Поэтому для получения гарантированного результата необходимо переходить к интервальным оценкам.Границы доверительного интервала для некоторых ракет-носителей представлены на рисунке 1.1

Рис.1.1 Оценки надежности ракет-носителей.
Методы расчета границ доверительного интервала будут рассмотрены в третьей главе пособия.
Общая теория надежности.
Общая теория надежности позволяет прогнозировать надежность различных изделий уже на этапе их проектирования, то есть до изготовления готовых образцов. Она основывается на анализе функционирования изделия и выявление условий его отказа. Согласно этой теории в рассмотрение водится функция работоспособности изделия ρ(t) с помощью которой записывается условие работоспособности, выполнение которого гарантирует безотказность изделия.
Например, при оценке вероятности не разрушения элемента конструкции в качестве функции работоспособности можно рассмотреть разность между действующими (σд) и допустимыми (σдоп) напряжениями
ρ(t) = σд(t) - σдоп(t) (1.11)
При этом условие работоспособности примет вид
ρ(t) < 0 ; 0 < t < T (1.12)
где Т – время функционирования изделия.
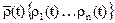 Условие работоспособности должно выполняться для каждого момента времени t. В данном случае предполагается, что ρ(t) является случайной функцией времени. В некоторых случаях ρ может не зависеть от времени, то есть является случайной величиной. Однако в наиболее общих ситуациях функция работоспособности надо предполагать векторной функцией . При этом под условием работоспособности понимаются принадлежность этой функции некоторой области допустимых значений Д .
Условие работоспособности должно выполняться для каждого момента времени t. В данном случае предполагается, что ρ(t) является случайной функцией времени. В некоторых случаях ρ может не зависеть от времени, то есть является случайной величиной. Однако в наиболее общих ситуациях функция работоспособности надо предполагать векторной функцией . При этом под условием работоспособности понимаются принадлежность этой функции некоторой области допустимых значений Д .
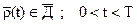 |

(1.13)
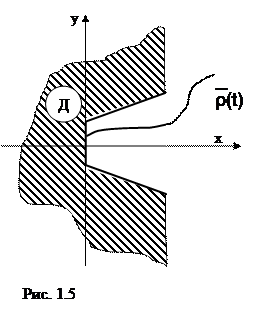
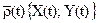 В частности, такие ситуации возникают при оценке вероятности безударного движения разделяемых объектов.Для определенности рассмотрим разделение 2х блоков, представленных на рис 1.4. Из анализа процесса разделения было выяснено, что элемент конструкции блока Б не должны достигать опасной зоны блока В, заштрихованной на рисунке. Допустим наибольшую опасность с точки зрения соударения представляют элементы конструкции блока Б, соответствующие т. А и А ́ (см. рис. 1.4). В дальнейшем будем рассматривать относительное движение точки А в системе координат ХУ с началом в т.О, совпадающей в начальный момент с т.А (рис. 1.5). При этом траектория движения т.А не должна пересекать границу области Д , представленных на рисунке. При построении области Д было учтено, что при движении т. А появляется опасность соударения с ней т. А . Таким образом, траектория движения точки А ограничена не только с верху, но и снизу. В данном случае областью допустимых траекторий т.А является область Д (незаштрихованная на рис. 1.5). Поэтому условия работоспособности, с точки зрения безударности разделения, можно представить в виде
В частности, такие ситуации возникают при оценке вероятности безударного движения разделяемых объектов.Для определенности рассмотрим разделение 2х блоков, представленных на рис 1.4. Из анализа процесса разделения было выяснено, что элемент конструкции блока Б не должны достигать опасной зоны блока В, заштрихованной на рисунке. Допустим наибольшую опасность с точки зрения соударения представляют элементы конструкции блока Б, соответствующие т. А и А ́ (см. рис. 1.4). В дальнейшем будем рассматривать относительное движение точки А в системе координат ХУ с началом в т.О, совпадающей в начальный момент с т.А (рис. 1.5). При этом траектория движения т.А не должна пересекать границу области Д , представленных на рисунке. При построении области Д было учтено, что при движении т. А появляется опасность соударения с ней т. А . Таким образом, траектория движения точки А ограничена не только с верху, но и снизу. В данном случае областью допустимых траекторий т.А является область Д (незаштрихованная на рис. 1.5). Поэтому условия работоспособности, с точки зрения безударности разделения, можно представить в виде
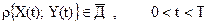 (1.14)
(1.14)
Здесь функция работоспособности есть вектор. После определения условия работоспособности надежность изделия оценивается по соотношению
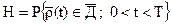
(1.15)
 Как показывают результаты исследований произвести оценку вероятности наиболее просто удается только в тех случаях, когда функция работоспособности является случайной величиной. Для случайных функций (даже одномерных) расчет можно произвести только для узких классов случайных процессов. В частности, даже для стационарных, нормальных процессов определить эту вероятность не удается. Поэтому для практических приложений используется приближенное соотношение, дающая достаточно хорошую точность для высоконадежных систем
Как показывают результаты исследований произвести оценку вероятности наиболее просто удается только в тех случаях, когда функция работоспособности является случайной величиной. Для случайных функций (даже одномерных) расчет можно произвести только для узких классов случайных процессов. В частности, даже для стационарных, нормальных процессов определить эту вероятность не удается. Поэтому для практических приложений используется приближенное соотношение, дающая достаточно хорошую точность для высоконадежных систем
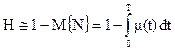 |
(1.16)
где M{N} – среднее число пересечений допустимой области;
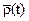 μ(t) – среднее число пересечений допустимой области в единицу времени.
μ(t) – среднее число пересечений допустимой области в единицу времени.
Величина μ(t) может быть найдена, если известны характеристики случайного процесса В заключении заметим, что для высоконадежных систем величина μ(t) может быть использована для оценки λ(t). Действительно, согласно формальной теории надежности
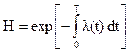 |
(1.17)
Разлагая экспоненту в ряд Тейлора и ограничиваясь линейным членом, получим
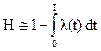 |
(1..18)
Сравнение соотношений (1.17; 1.18) показывает, что можно приближено принять
λ(t) ≈ μ(t) (1.19)
При этом надо помнить, что физический смысл этих параметров совершено различный.
Сложность аналитического представления для μ(t) ограничивает возможность использования этого подхода.
Существенное упрощение расчетов, как в одномерном, так и в многомерном случае дает переход от случайных процессов к случайным величинам. Это оказывается возможным, когда будут найдены моменты времени, соответствующие наиболее тяжелым условиям работы изделия. При этом функция работоспособности анализируется не для всего периода функционирования изделия, а в определенные известные моменты времени. Таким образом, условия работоспособности пишутся в виде
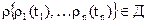 (1.20)
(1.20)
где ρi(ti) – некоторые случайные величины.
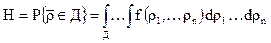 Тогда надежность изделия, оцениваемая вероятность выполнения условия (2.20) будет равна
Тогда надежность изделия, оцениваемая вероятность выполнения условия (2.20) будет равна
(1.21)
где f(ρ1… ρn) – совместная плотность распределения случайных величин ρ1, ρ2,…ρn. Для одномерного случая соотношение упроститься:
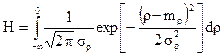 |
(1.22)
Элементов.
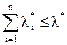 При использовании метода предполагается, что подсистемы соединены последовательно и имеют постоянную интенсивность отказов, что отказ любой подсистемы вызывает отказ всей системы и что заданная наработка подсистем равна заданной наработке системы. При использовании этого метода необходимо выразить требуемую надежность через интенсивности отказов. Задача состоит в том, чтобы выбрать такие λ*i, что
При использовании метода предполагается, что подсистемы соединены последовательно и имеют постоянную интенсивность отказов, что отказ любой подсистемы вызывает отказ всей системы и что заданная наработка подсистем равна заданной наработке системы. При использовании этого метода необходимо выразить требуемую надежность через интенсивности отказов. Задача состоит в том, чтобы выбрать такие λ*i, что
где λ*i – заданная интенсивность отказов i-ой подсистемы, а λ*– требуемая интенсивность отказов системы.
Метод включает следующие этапы:
1. Определение интенсивности отказов подсистем λi по результатам наблюдений или на основе оценок по данным за прошлое время.
2. Задание весового множителя ωi для каждой подсистемы в соответствии с интенсивностями отказов, определенными на этапе 1; ωi определяется по формуле
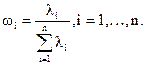 |
3. Вычисление требуемой интенсивности отказов подсистемы с помощью соотношения
λ*i = ωiλ* , i = 1, …, n.
Ясно, что этот метод позволяет задать новые значения интенсивности отказов на основе весовых множителей, которые являются функциями интенсивностей отказов подсистем за прошлое время.
Нормирование надежности при структурном резервировании
элементов системы.
При использовании уже существующих элементов, задача обеспечения заданных уровней надежности системы может быть решена использованием структурного резервирования.
При решении поставленной задачи примем, что вероятность безотказной работы нерезервированного i-ого элемента 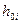 за период Tr оценивается по произвольному закону распределения F(x) h 0i = 1 – F(Tr)
за период Tr оценивается по произвольному закону распределения F(x) h 0i = 1 – F(Tr)
Соответственно вероятность отказа i-ого нерезервированного элемента будет равна
q0i = 1 – h0i.
При структурном резервировании вероятность отказа i-го элемента 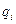 , может быть замещением отказавшего элемента («холодный» резерв)
, может быть замещением отказавшего элемента («холодный» резерв)
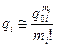 ,
,
где 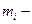 общее число элементов в резервной группе ( кратность резерва ).
общее число элементов в резервной группе ( кратность резерва ).
Производя логарифмирование, получим
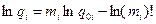 .
.
В дальнейшем соотношение представим в виде
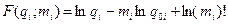
Затраты на производство и эксплуатацию i-ого элемента системы будут равны
СЭi = C0imi,
где СЭi – стоимость i-ой системы.
Полученные результаты позволяют перейти к решению задачи нормирования надежности элементов, то-есть оптимального распределения уровней надежности между отдельными элементами системы, обеспечивающих удовлетворение заданных требований к надежности системы в целом при минимальном расходе средств на реализацию целевой программы. Очевидно, затраты на производство и эксплуатацию системы, состоящей из n элементов, будут равны
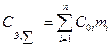 .
.
Соответственно надежность системы, состоящей из n
последовательно соединенных элементов, будет равна
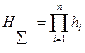 .
.
Для высоконадежных систем вероятность отказа можно оценить по приближенному соотношению
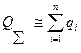 ,
,
где qi = 1 – hi.
Очевидно заданные требования к надежности системы могут быть обеспечены при различных комбинациях значений слагаемых qi. Среди множества значений qi целесообразно выбрать такие, которые обеспечивают минимум затрат на реализацию целевой программы. Поставленную задачу будем решать методом Лагранжа.
В рассматриваемом случае функция Лагранжа примет вид
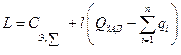 ,
,
где l – множитель Лагранжа.
При этом оптимальные уровни qi, должны удовлетворять условию 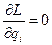 .
.
Раскрывая выражение производной, получим 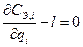 ,
,
Производная от затрат по qi оценивается по соотношению
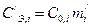 ,
,
где 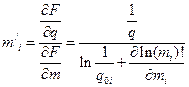 .
.
Для нахождения производной воспользуемся приближенной оценкой функционала m!.
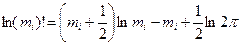
Предполагая, что дискретная функция 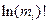 может быть аппроксимирована непрерывной зависимостью, проведем формальное дифференцирование
может быть аппроксимирована непрерывной зависимостью, проведем формальное дифференцирование
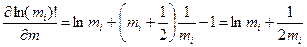 .
.
Таким образом, окончательно получим
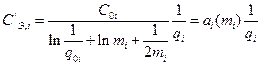 ,
,
где 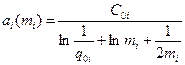 .
.
После подстановки 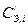 в условие оптимальности найдем
в условие оптимальности найдем 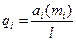 .
.
С учетом выражения для 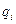 дисциплинирующее условие примет вид
дисциплинирующее условие примет вид
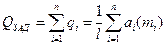 . .
. .
Разрешая это соотношение относительно неопределенного множителя Лагранжа , найдем
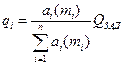 .
.
Окончательный результат можно получить методом последовательных приближений. В качестве нулевого приближения можно принять равномерное распределение надежности
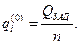 .
.
Значение 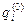 позволяет найти оценку
позволяет найти оценку 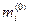 из соотношения
из соотношения 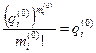 .
.
Итерационный процесс заканчивается по достижении требуемой точности вычислений.
В случае «горячего» резерва, при проведении расчетов, следует принять
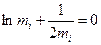 .
.
Отсюда 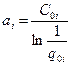 .
.
При этом кратность резерва рассчитывается по соотношению
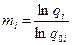 ,
,
где 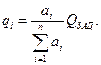
Лекция № 7
Планирование автономной отработки элементов систем.
При использовании оригинальных, то-есть вновь разрабатываемых элементов систем, поставленная задача сводится к обоснованию уровней параметрической избыточности, закладываемых на этапе проектной разработки отдельных элементов, а так же объемов их экспериментальной отработки. В дальнейшем рассмотрим решение этой задачи для случая нормального закона распределения параметров работоспособности устройства .
При решении поставленной задачи будем предполагать, что РН может быть представлена в виде системы с последовательно соединенными элементами. В этом случае надежность системы H равна
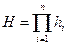 , где hi – надежность i-го элемента.
, где hi – надежность i-го элемента.
Для высоконадежных систем имеем
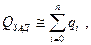 где qi =1- hi.- вероятность отказа i- го элемента.
где qi =1- hi.- вероятность отказа i- го элемента.
Соответственно точечная оценка вероятности отказа будет равна
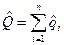 , где
, где 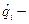 точечная оценка вероятности отказа i-го элемента.
точечная оценка вероятности отказа i-го элемента.
Для расчета верхней границы вероятности отказа системы 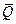 можно воспользоваться интервальной оценкой
можно воспользоваться интервальной оценкой
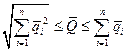 , (3.18)
, (3.18)
где  ;
; 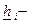 нижняя граница надежности i-го элемента системы.
нижняя граница надежности i-го элемента системы.
Нижняя граница надежности элемента 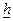 , прогнозируемая после проведении k испытаний , в случае нормального распределения параметров работоспособности, может быть оценена по соотношению
, прогнозируемая после проведении k испытаний , в случае нормального распределения параметров работоспособности, может быть оценена по соотношению
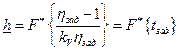 ,
,
где 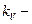 коэффициент вариации коэффициента параметрического запаса
коэффициент вариации коэффициента параметрического запаса 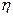 ;
;
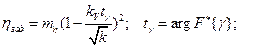
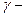 уровень доверительной вероятности;
уровень доверительной вероятности;
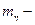 математическое ожидание коэффициента запаса; k- число испытаний;
математическое ожидание коэффициента запаса; k- число испытаний;
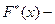 функция нормированного нормального распределения .
функция нормированного нормального распределения .
Таким образом потребный уровень математического ожидания коэффициента запаса удовлетворяет соотношению
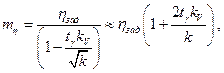
После преобразований будем иметь
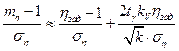 ,
,
Введя обозначения 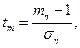
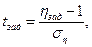
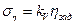 ,
,
получим 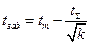 .
.
Таким образом 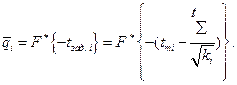 , где
, где 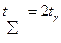 .
.
Следовательно, требуемый уровень надежности может быть подтвержден при различных комбинациях параметров tmi и 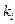 . Среди многообразия этих значений целесообразно выбрать те, которые обеспечивают заданный уровень вероятности отказа при минимальных затратах средств.
. Среди многообразия этих значений целесообразно выбрать те, которые обеспечивают заданный уровень вероятности отказа при минимальных затратах средств.
Очевидно, уровень избыточности элементов системы tmi будет определять производственные и эксплуатационные расходы на выполнение программы:
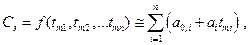
где 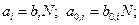 N – объем выпускаемой продукции;
N – объем выпускаемой продукции;
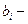 коэффициент чувствительности, характеризующий удельные затраты
коэффициент чувствительности, характеризующий удельные затраты
на обеспечение единицы надежности, выраженной в гауссах.
Параметр 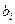 определяется уровнем избыточности элемента. В частности, при использовании «горячего» резерва вероятность отказа резервной группы
определяется уровнем избыточности элемента. В частности, при использовании «горячего» резерва вероятность отказа резервной группы 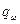 оценивается по соотношению
оценивается по соотношению
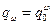 ,
,
где 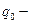 вероятность отказа нерезервированного элемента;
вероятность отказа нерезервированного элемента; 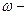 условная кратность резерва.
условная кратность резерва.
Отсюда 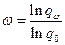 .
.
Очевидно стоимость резервированного элемента будет равна
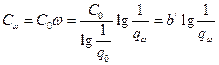 ,
,
где 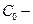 стоимость нерезервированного элемента;
стоимость нерезервированного элемента;
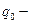 вероятность отказа нерезервированного элемента;
вероятность отказа нерезервированного элемента;
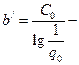 затраты на единицу надежности, выраженной в беллах.
затраты на единицу надежности, выраженной в беллах.
Переходя к оценке надежности в гауссах, получим
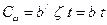 , где
, где 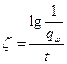 ;
; 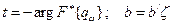 .
.
Очевидно параметр b характеризует удельные затраты на единицу надежности, выраженной в гауссах.
Зависимость стоимости от кратности резерва можно представить в виде
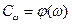
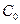 .
.
Вид функции 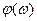 зависит от типа резервирования .Очевидно, в случае «горячего» резерва , имеем
зависит от типа резервирования .Очевидно, в случае «горячего» резерва , имеем 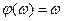 .
.
. Для «холодного» резерва стоимость резервной группы представим в виде
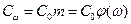 ,
,
где m – общее число элементов в резервной группе.
Отсюда 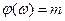 .
.
Для нахождения m воспользуемся приближенной оценкой 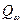
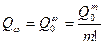 .
.
.
После логарифмирования, получим
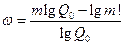 .
.
При решении задачи дискретную функцию 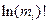 аппроксимируем непрерывной зависимостью. В дальнейшем проанализируем характер изменения
аппроксимируем непрерывной зависимостью. В дальнейшем проанализируем характер изменения  по
по 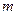 для
для 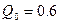 . .Расчеты проводились по программе Mathcad. При написании программы были приняты следующие обозначения:
. .Расчеты проводились по программе Mathcad. При написании программы были приняты следующие обозначения: 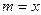 ,
, 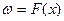 . Функция F(x) рассчитывалась по соотношению
. Функция F(x) рассчитывалась по соотношению

При проведении практических расчетов зависимость F(x), в окрестности оптимального решения, можно аппроксимировать прямой
. 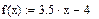
Таким образом, для рассматриваемого случая, можно принять
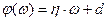 , где
, где 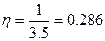 .
.
Функции F(x) и f(x) представлены на рис. 3.4.
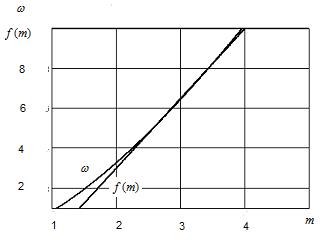
Рис. 3.4. Зависимость кратности резерва  и аппроксимирующей прямой
и аппроксимирующей прямой 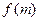
от общего числа элементов в резервной группе 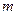 .
.
В дальнейшем найдем аналогичные соотношения для элементов с параметрической избыточностью. При решении поставленной задачи, вероятность отказа элементов с параметрической избыточностью условно представим в виде
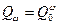
где 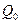 - вероятность отказа элемента, соответствующая коэффициенту запаса
- вероятность отказа элемента, соответствующая коэффициенту запаса 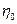 ;
; 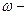 условная кратность резерва.
условная кратность резерва.
Согласно результатам, полученным в работе [ 7 ], надежность элемента 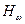 ,прогнозируемая после проведении k испытаний , может быть оценена по соотношению
,прогнозируемая после проведении k испытаний , может быть оценена по соотношению
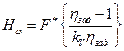 ,
,
где 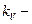 коэффициент вариации коэффициента запаса;
коэффициент вариации коэффициента запаса;
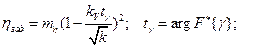
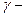 уровень доверительной вероятности;
уровень доверительной вероятности;
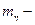 математическое ожидание коэффициента запаса.
математическое ожидание коэффициента запаса.
Знание 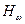 , позволяет оценить условную кратность резерва
, позволяет оценить условную кратность резерва
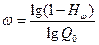 ,
,
В дальнейшем будем считать, что стоимость резервированного элемента пропорциональна коэффициенту запаса 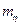 . Тогда функцию
. Тогда функцию 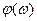 можно оценить по соотношению
можно оценить по соотношению 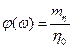 .
.
Характер изменения функции 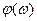 представлен на рис. 3.5
представлен на рис. 3.5
.
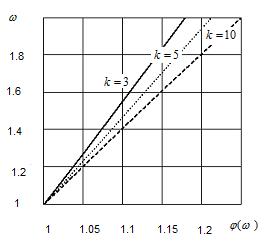
Рис.3.5 Характер зависимости кратности резерва  для различных
для различных 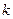 от функции
от функции
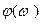 для элементов с параметрической избыточностью.
для элементов с параметрической избыточностью.
При построении графика были приняты следующие исходные данные:
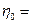 1.3 ;
1.3 ; 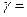 0,95 ;
0,95 ; 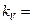 0,1 ;
0,1 ; 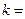 3, 5, 10.
3, 5, 10.
Как видно из графика функция 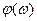 слабо зависит от объема испытаний k . Приближенно для функции
слабо зависит от объема испытаний k . Приближенно для функции 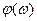 =
= 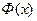 может быть принята линейная аппроксимационная зависимость
может быть принята линейная аппроксимационная зависимость
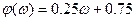 (
( 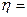 0.25).
0.25).
.
С учетом полученных результатов, выражение для стоимости примет вид
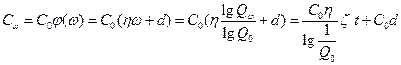 ,
,
где 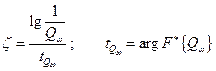
Отсюда
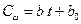 , где
, где 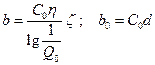 .
.
Для рассмотренного в примере случая : 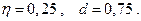
Соответственно затраты на экспериментальную отработку будут определяться объёмами испытаний элементов
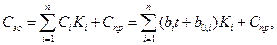
где Ci - затраты на проведение одного испытания i-го элемента,
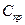 – затраты, не зависящие от варьирующихся параметров.
– затраты, не зависящие от варьирующихся параметров.
Таким образом, решение задачи сводится к минимизации функции суммарных затрат
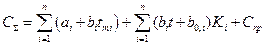 (3.19)
(3.19)
В качестве дисциплинирующего условия рассмотрим правую границу неравенства (3.18)
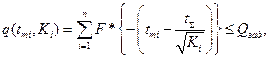
В дальнейшем для нахождения оптимального решения задачи рассмотрим функцию Лагранжа
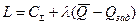
Оптимальные параметры будут удовлетворять системе алгебраических уравнений:
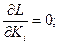
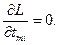
При нахождении производной 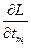 , предполагая, что число испытаний
, предполагая, что число испытаний 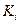 существенно меньше объема транспортной программы N, вторым слагаемым в выражении (2.36) можно пренебречь. Поэтому в дальнейшем удельные затраты на проведение одного испытания
существенно меньше объема транспортной программы N, вторым слагаемым в выражении (2.36) можно пренебречь. Поэтому в дальнейшем удельные затраты на проведение одного испытания 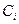 будем считать постоянными для каждого i-го элемента системы.
будем считать постоянными для каждого i-го элемента системы.
Производя дифференцирование, получим:
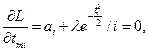
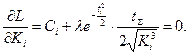 (3.20)
(3.20)
Разрешая систему уравнений относительно Ki, найдем
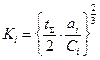 (3.21)
(3.21)
Соотношение (3.21) позволяет оценить оптимальный объем испытаний с точностью до целых. Таким образом оптимальные объемы испытаний отдельных элементов не зависят от требований, предъявляемых к надежности систем и определяются соотношением удельных затрат на обеспечение единицы надежности, закладываемой на этапе проектирования, 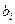 и затрат на проведение одного испытания
и затрат на проведение одного испытания 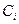 .
.
Соответственно, из первого уравнения системы (3.20) получим:
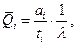
где 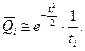
Подставляя 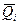 в граничное условие , приходим к соотношению:
в граничное условие , приходим к соотношению: 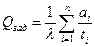 . Отсюда
. Отсюда 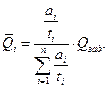 (3.22)
(3.22)
Таким образом, оптимальные уровни вероятности отказа пропорциональны удельным затратам 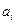 и заданным требованиям к вероятности отказа системы
и заданным требованиям к вероятности отказа системы 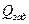 .
.
Заметим, что предположение о постоянстве 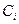 , принятое выше, может не выполняться при создании единичных КА, затраты на разработку и экспериментальную отработку которых, существенно превышают затраты на изготовление и применение этих комплексов. Они могут составлять до 70% от общих затрат на всю программу. В этом случае решение должно быть уточнено.
, принятое выше, может не выполняться при создании единичных КА, затраты на разработку и экспериментальную отработку которых, существенно превышают затраты на изготовление и применение этих комплексов. Они могут составлять до 70% от общих затрат на всю программу. В этом случае решение должно быть уточнено.
Лекция №11
В случае экспоненциального распределения наработки на отказ нижняя граница надежности элемента равна
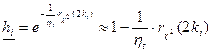 ,
,
где 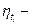 коэффициент временного запаса.
коэффициент временного запаса.
Характер изменения функции 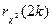 представлен на рис. 3.6 При построении графика были приняты следующие обозначения:
представлен на рис. 3.6 При построении графика были приняты следующие обозначения: 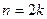 ,
, 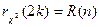 ,
, 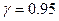 .
.
Расчеты проводились по соотношению [8]:
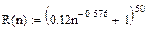 (3.23)
(3.23)
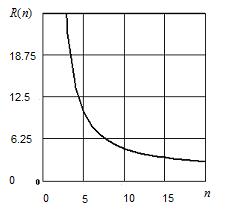
Рис. 3.6 Зависимость функции 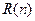 от параметра
от параметра 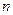 .
.
Очевидно, что 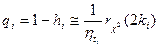
В общем случае надежность технической системы будет определяться уровнями надежности отдельных элементов, входящих в ее состав и типом их соединения. При последовательно соединении элементов вероятность отказа технической системы приближенно можно оценить по соотношению
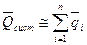 где
где 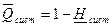 .
.
Отсюда получим
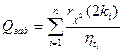 (3.24)
(3.24)
где 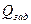 - заданная вероятность отказа системы.
- заданная вероятность отказа системы.
Следовательно, требуемый уровень надежности системы может подтвержден при различных комбинациях параметров 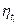 и
и 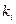 . Среди многообразия значений
. Среди многообразия значений 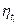 и
и 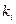 целесообразно выбрать те, которые обеспечивают заданный уровень надежности при минимальных затратах.
целесообразно выбрать те, которые обеспечивают заданный уровень надежности при минимальных затратах.
Очевидно, уровни избыточности элементов системы mti будут определять эксплуатационные расходы на выполнение программы
