Алгоритм Евклида для целых чисел
Укажем процедуру нахождения наибольшего общего делителя, которая в геометрической форме описана еще в «Началах». Даны числа 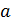 и
и 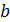 ,
, 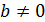 . Делим
. Делим 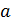 на
на 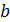 и получаем остаток
и получаем остаток 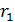 ,
, 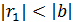 . Далее делим
. Далее делим 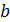 на
на 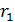 , и получаем остаток
, и получаем остаток 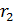 ,
, 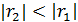 . Продолжаем далее до тех пор, пока не получим нулевой остаток. Утверждается, что последний ненулевой остаток есть НОД(
. Продолжаем далее до тех пор, пока не получим нулевой остаток. Утверждается, что последний ненулевой остаток есть НОД( 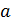 ,
, 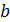 ). Для доказательства рассмотрим цепочку равенств:
). Для доказательства рассмотрим цепочку равенств:
1 ) 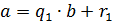 ,
,
2 ) 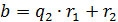 ,
,
3) 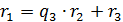 ,
,
4) 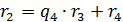 ,
,
5) 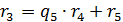 ,
,
6) 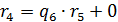 ,
,
в которой для определенности шестой остаток равен нулю, а пятый отличен от нуля. Проверим, что 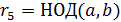 . Сначала убедимся, что
. Сначала убедимся, что 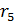 есть общий делитель чисел
есть общий делитель чисел 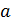 и
и 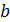 . Из формулы (6) видно, что
. Из формулы (6) видно, что 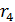 делится на
делится на 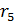 . Тогда из (5) заключаем, что
. Тогда из (5) заключаем, что 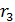 делится на. Поднимаясь по цепочке, видим, что
делится на. Поднимаясь по цепочке, видим, что 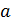 и
и 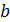 делятся на
делятся на 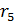 . Далее пусть δ – какой-нибудь общий делитель чисел
. Далее пусть δ – какой-нибудь общий делитель чисел 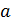 и
и 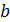 . Равенство (1) показывает, что остаток
. Равенство (1) показывает, что остаток 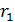 тоже делится на δ. Тогда из (2) заключаем, что и
тоже делится на δ. Тогда из (2) заключаем, что и 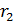 делится на δ. Спускаясь по цепочке, находим, что и
делится на δ. Спускаясь по цепочке, находим, что и 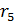 делится на δ, что и требовалось.
делится на δ, что и требовалось.
С помощью алгоритма Евклида легко установить линейное представление  через
через 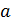 и
и 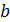 . Действительно, равенство (5) показывает, что
. Действительно, равенство (5) показывает, что 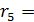
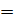
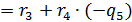 , то есть
, то есть 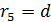 можно линейно выразить через
можно линейно выразить через 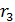 и
и 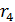 . Но из (4) видно, что
. Но из (4) видно, что 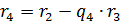 , а тогда
, а тогда 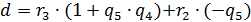 , то есть
, то есть 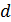 можно линейно выразить через
можно линейно выразить через 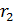 и
и 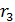 . Поднимаясь по цепочке вверх, находим, что окончательно
. Поднимаясь по цепочке вверх, находим, что окончательно 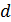 выражается через
выражается через 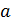 и
и 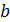 . Иными словами, найдутся такие целые числа
. Иными словами, найдутся такие целые числа 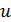 и
и 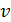 , что
, что 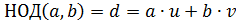 .
.
Это представление наибольшего общего делителя двух чисел называется соотношением Безу, а числа 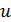 и
и 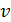 – коэффициентами Безу. Соотношение Безу было ключевым в доказательстве теоремы Евклида и основной теоремы арифметики.
– коэффициентами Безу. Соотношение Безу было ключевым в доказательстве теоремы Евклида и основной теоремы арифметики.
Пример
Для иллюстрации, алгоритм Евклида будет использован, чтобы найти  , для a = 1071 и b = 462. Сначала от 1071 нужно отнимать 462 до тех пор, пока не получим число, меньшее 462. В данном случае эту операцию нужно проделать дважды, следовательно, q1 = 2, остаток
, для a = 1071 и b = 462. Сначала от 1071 нужно отнимать 462 до тех пор, пока не получим число, меньшее 462. В данном случае эту операцию нужно проделать дважды, следовательно, q1 = 2, остаток  .
.
1071 = 2 ∙ 462 + 147.
Затем от 462 отнимем число кратное 147 так, чтобы разность была меньше чем 147. q2 = 3, остаток 21.
462 = 3 147 + 21.
Далее 147 = 7 ∙ 21 + 0.
Так как последний остаток равен нулю, алгоритм заканчивается и НОД(1071, 462) = 21.
Подобные слагаемые
Для любых чисел а, b и с верны равенства:
 | (1) |
 | (2) |
 | (3) |
 | (4) |
 | (5) |
 | (6) |
 | (7) |
 | (8) |
 | (9) |
 | (10) |
 | (11) |
С помощью этих равенств можно упрощать буквенные выражения. Например,  .
.
Слагаемые  содержат одинаковые буквенные множители. Такие слагаемые называют подобными. Числовой множитель в произведении вида 7х называют коэффициентом.
содержат одинаковые буквенные множители. Такие слагаемые называют подобными. Числовой множитель в произведении вида 7х называют коэффициентом.
Пользуясь распределительным законом, можно упрощать выражения, содержащие подобные слагаемые. Например, упростим выражения:




Такое упрощение выражений называют приведением подобных слагаемых. Чтобы привести подобные слагаемые, надо сложить их коэффициенты и полученное число умножить на общий буквенный множитель.
В простых случаях промежуточные вычисления опускают, например, пишут:  .
.
Если слагаемых больше двух, то при приведении подобных слагаемых бывает полезно группировать отдельно слагаемые с коэффициентами разных знаков.
Например, 

[1] Здесь представлен краткий конспект соответствующих разделов учебника: Арифметика, 5 / С. М. Никольский, М. К. Потапов, Н. Н. Решетников, А. В. Шевкин. – М.: Просвещение, 1999. – 255 с. Нумерация разделов такая же, как и в учебнике.
[2] Краткий конспект по данной теме составлен на основании соответствующих разделов учебника: Арифметика, 6 / С. М. Никольский, М. К. Потапов, Н. Н. Решетников, А. В. Шевкин. – М.: Просвещение, 2000. – 270 с.
