Расчетная модель к теореме Кастильяно.

При переходе от состояния 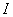балки к состоянию 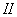все нагрузки Р опустятся, значит, их потенциальная энергия уменьшится. Так как равновесие не нарушалось, то уменьшение, энергии нагрузок 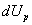целиком преобразовалось в увеличение потенциальной энергии деформаций балки dU. Величина 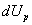измеряется работой внешних сил при переходе балки из положения 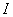в положение II:

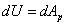
Изменение dU потенциальной энергии деформации, являющейся функцией сил , , ,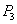..., произошло за счет очень малого приращения одной из этих независимых переменных , поэтому дифференциал такой сложной функции равен:

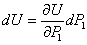
Что касается величины 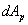, то эта работа в свою очередь является разностью работы нагрузок Р для положени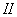й и :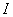

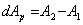
Работа при одновременном и постепенном возрастании сил Р равна:

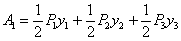
При вычислении работы 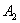учтем, что ее величина всецело определяется окончательной формой деформированной балки и не зависит от порядка, в котором производилась нагрузка.

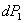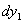
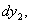
Предположим, что мы сначала нагрузили нашу балку грузом ; балка очень немного прогнется (Рис.2, положение III), и прогибы ее в точках 1, 2, 3 будут 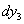. Работа статически приложенной нагрузки 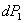будет равна 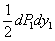. После этого начнем постепенно нагружать балку одновременно возрастающими грузами , , .

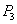Рис.2. Расчетная модель к теореме Кастильяно.

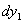
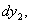
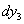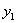
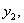
К первоначальным прогибам добавятся прогибы 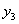(Рис.2). При этой стадии нагружения силы , , 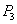произведут работу 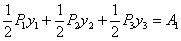, кроме этого, произведет работу уже находившийся на балке груз 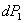; он пройдет путь 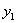, и так как при втором этапе нагружения он оставался постоянным, то его работа равна 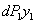Балка займет положение 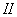, показанное на Рис.2 пунктиром.

Таким образом, полная работа, проделанная внешними нагрузками при переходе балки из недеформированного состояния в положение 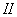, будет равна.

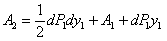
Теперь вычислим

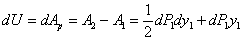
Пренебрегая слагаемым второго порядка малости, получаем:

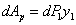
Подставляя полученные значения dU и 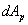в исходное уравнение, находим

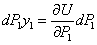
или

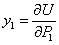
Таким образом, в рассмотренном случае прогиб точки приложения сосредоточенной силы , равен частной производной потенциальной энергии деформации по этой силе.

Полученный результат можно обобщить. Пусть на балку помимо сосредоточенных сил Р действуют в разных сечениях еще пары сил М (Рис.3). Мы можем повторить предыдущие рассуждения, считая, что балка переводится из положения 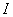в положение 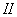путем добавки 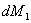к паре 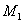. Весь ход рассуждений остается без изменений, надо будет лишь при вычислении работы моментов 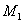, 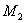... умножать их не на прогибы, а на углы поворота 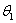, ,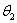... тех сечений, где эти пары приложены. Тогда dU будет равно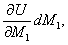 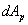станет 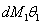, и в итоге получим:

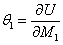
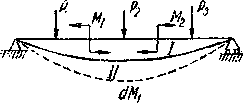
Рис.3. Обобщенная расчетная модель к теореме Кастильяно.

Так как 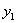— это перемещение, соответствующее силе , a 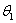— перемещение, соответствующее силе 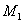то полученные нами результаты можно формулировать так: производная потенциальной энергии деформации по одной из независимых внешних сил равна перемещению, соответствующему этой силе. Это и есть так называемая теорема Кастильяно, опубликованная в 1875 г.

Заметим, что присутствие на балке сплошной нагрузки не меняет предыдущих выводов, так как всякую сплошную нагрузку можно рассматривать как состоящую из большого числа сосредоточенных сил.

Предыдущий вывод был сделан для балки, но совершенно ясно, что его можно повторить для любой конструкции, деформации которой следуют закону Гука.

Для случая изгиба нами была получена формула, связывающая величину потенциальной энергии U с изгибающими моментами:

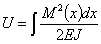
Изгибающий момент является линейной функцией нагрузок , …, , 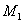,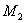..., q, приложенных к балке:

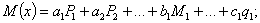
в этом легко убедиться, просмотрев формулы для вычисления изгибающих моментов при построении эпюр. Следовательно, потенциальная энергия является функцией второй степени от независимых внешних нагрузок.

Вычислим частную производную от U по одной из внешних сил, например . Получаем:

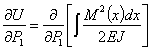
Здесь мы имеем дело с так называемым дифференцированием определенного интеграла по параметру, так как М(х)— функция и и х, интегрирование производится по х, а дифференцирование по параметру . Как известно, если пределы интеграла постоянны, то следует просто дифференцировать подинтегральную функцию.

Таким образом, прогиб в точке приложения сосредоточенной силы равен:

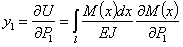
а угол поворота сечения с парой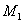

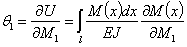
Напомним, что знак предела l условно показывает, что интеграл должен охватить всю балку.

Примеры приложения теоремы Кастильяно.

Определим (Рис.4) прогиб свободного конца В балки, защемленной другим концом А. Балка нагружена сосредоточенной силой, приложенной в точке В. В данном случае возможно непосредственное применение теоремы Кастильяно, так как отыскивается прогиб сечения, где приложена сосредоточенная сила Р

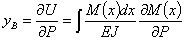
Рис.4. Пример расчетной схемы для расчета перемещений.

Начало отсчета абсциссы х сечения можно выбирать произвольно, лишь бы формула для М (х) была возможно проще. Отсчитывая х от точки В, получаем для момента в любом сечении балк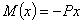и

и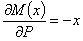

Подставляя эти значения в формулу для 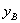и интегрируя, чтобы охватить всю длину балки от 0 до l, получаем:

Лекция № 34. Теоремы о взаимности работ и Максвелла — Мора.

Пользуясь понятием о потенциальной энергии, можно установить следующую зависимость между деформациями в различных сечениях балки.

Если к балке, нагруженной силой приложить затем статически силу в сечении 2, то к прогибу точки приложения силы от этой же силы 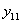прибавится (Рис.1) прогиб от силы , равный 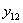; первый значок у буквы у указывает точку, для которой вычисляется прогиб; второй — обозначает силу, вызывающую этот прогиб.

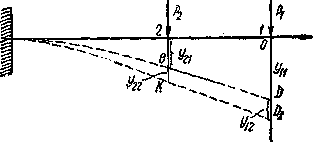
Рис.1. Расчетная схема к теореме о взаимности работ

Полная работа внешних сил составится из трех частей: работы силы на вызванном ею прогибе 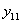, т. е. 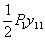, работы силы на вызванном ею прогибе ее точки приложения 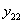, т. е. 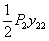, наконец, работы силы на прогибе ее точки приложения от силы , т. е. .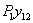

Таким образом, накопленная в стержне при действии обеих сил энергия будет равна:

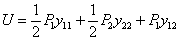
Это количество энергии деформации зависит лишь от конечных значений сил и прогибов и не зависит от порядка нагружения.

Если к балке, загруженной силой , приложить затем силу то, повторив цепь вычислений, получим:

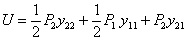
Сравнивая оба значения U, получаем:

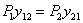
т. е. работа силы (или первой группы сил) на перемещениях, вызванных силой (второй группой сил), равна работе силы на перемещениях, вызванных силой .

Это и есть теорема о взаимности работ. Ее можно сформулировать и иначе: работа первой силы ( ) при действии второй ( ) равна работе второй силы при действии первой.

Теорема Максвелла—Мора.

Прогиб балки в точке приложения сосредоточенной силы Р равен:

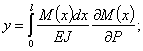
аналогичное выражение мы имеем и для угла поворота с заменой производной 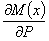на 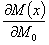. Выясним, что представляют собой эти производные.

Если на балке расположена какая угодно нагрузка из сосредоточенных сил , , ,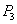..., моментов 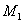, ,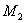..., сплошных нагрузок 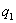, 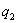..... то момент М(х) в любом сечении такой балки выражается линейной функцией от нагрузок:

Рис.2. Частная расчетная модель метода Максвелла — Мора.

Коэффициенты 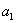, ,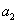..., , 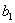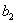…, , 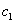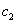... являются функциями пролета балки, расстояний точек приложения сил и моментов от опор и абсциссы х взятого сечения. Пусть мы отыскиваем прогиб точки приложения силы ; тогда

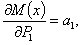
так как , ,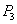..., , 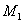,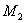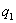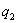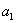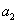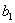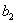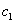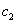..., , ..., , ,..., , …, , ... при этом дифференцировании постоянны. Но 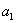можно рассматривать как численную величину момента М в любом сечении балки от действия так называемой единичной нагрузки, т. е. силы 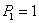; действительно, подставляя в формулу вместо его частное значение, единицу, и приравнивая все остальные нагрузки нулю, получаем .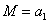

Например, для балки, изображенной на Рис2, а, изгибающий момент равен:

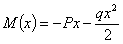
Производная 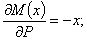; но это как раз и будет выражение изгибающего момента нашей балки, если мы ее нагрузим силой 1, приложенной в той же точке В, где расположена сила Р (Рис.2, б), и направленной в ту же сторону.

Аналогично, производная изгибающего момента М (х) по паре сил 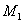численно представляет собой изгибающий момент от пары с моментом, равным единице, приложенной в том же сечении, где имеется пара 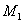, и направленной в ту же сторону. Таким образом, вычисление производных изгибающего момента можно заменить вычислением изгибающих моментов от единичной нагрузки. Эти моменты мы будем обозначать буквой .

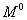Таким образом, для отыскания перемещения 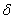(прогиба или угла поворота) любого сечения балки, вне зависимости от того, приложена или не приложена в этом сечении соответствующая сила, необходимо найти выражение для изгибающего момента М от заданной нагрузки и момента 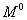от соответствующей единичной нагрузки, приложенной в сечении, где ищем перемещение 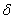; тогда это перемещение выразится формулой

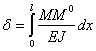
Эта формула была предложена Максвеллом в 1864 г. и введена в практику расчета О. Мором в 1874 г. Если мы в полученном выражении под 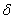подразумеваем прогиб, то момент 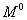надо вычислять от сосредоточенной единичной силы, приложенной в той точке, где мы отыскиваем прогиб; при вычислении же угла поворота в качестве единичной нагрузки прикладывается пара сил с моментом, равным единице.

Для примера рис.2 имеем:

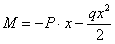	(рис.2,а)
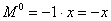	(рис.2, б)

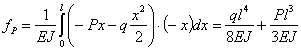
Знак плюс означает, что направление перемещения совпадает с направлением единичной нагрузки, знак минус — наоборот.

Если при определении изгибающих моментов придется делить балку на участки, то соответственно и интеграл в формуле распадется на сумму интегралов.

Сравнивая формулу Кастильяно с формулой Мора, нетрудно заметить, что они отличаются лишь одним множителем. В теореме Кастильяно 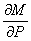или 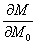, в теореме Мора .

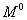Следовательно, производная от изгибающего момента по обобщенной силе — это то же самое, что изгибающий момент от силы .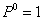

Метод Верещагина.

Способ Максвелла — Мора в значительной степени вытеснил на практике непосредственное применение теоремы Кастильяно. В справочниках обычно приводятся таблицы интегралов 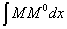для наиболее часто встречающихся типов нагрузки.

Наш соотечественник А. Н. Верещагин в 1924 г. предложил упрощение вычислений. Так как единичной нагрузкой бывает обычно либо сосредоточенная сила, либо пара сил, то эпюра 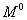оказывается ограниченной прямыми линиями. Тогда вычисление 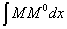при любом очертании эпюры М можно произвести следующим образом. Пусть эпюра М (Рис.3) имеет криволинейное очертание, а эпюра 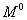— прямолинейное. Произведение Mdx можно рассматривать, как элемент 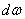площади эпюры М, заштрихованный на чертеже.

Так как ординат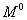а равна 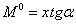, то произведение 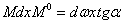, а весь интеграл 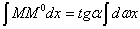представляет собой статический момент площади эпюры М относительно точки А, умноженный на .

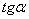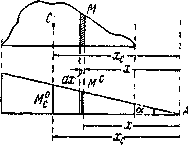
Рис.3. Расчетная модель метода Верещагина.

Но этот статический момент равен всей площади 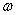эпюры М, умноженной на расстояние от ее центра тяжести 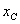до точки А. Таким образом,

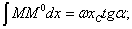
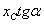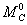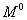но величина равна ординате эпюры под центром тяжести эпюры М. Отсюда

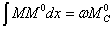
и искомое перемещение равно

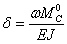
Таким образом, для определения перемещения 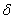надо вычислить 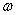— площадь эпюры М, умножить ее на ординату 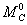эпюры от единичной нагрузки под центром тяжести площади 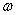и разделить на жесткость балки.

Определим этим способом угол поворота сечения D балки, изображенной на Рис.4, а; Балка загружена моментом М, приложенным в сечении В к консоли АВ. Эпюра М показана на Рис.4, б. Прикладываем в сечении D единичную пару, выбирая ее направление произвольно (Рис.4, в). Эпюра моментов от единичной нагрузки показана на рис.4, г. Так как М на участках DC и СВ равен нулю, то остается лишь один интеграл для участка АВ.

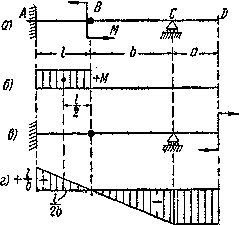
а) расчетная схема б)грузовая эпюра в)фиктивное состояние г) эпюра моментов от единичного момента

Рис.4. Иллюстрация метода Верещагина:

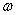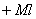Площадь равна ; ордината эпюры 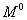под центром тяжести площади 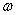равна 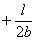отсюда искомый угол поворота 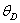равен

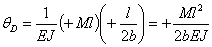
Знак плюс показывает, что вращение происходит по направлению единичной пары, т. е. по часовой стрелке.

Лекция № 35. Расчет статически неопределимых балок. Способ сравнения деформаций.