МАТЕМАТИЧЕСКИЙ РЕДАКТОР MathCad
МАТЕМАТИЧЕСКИЙ РЕДАКТОР MathCad
Методические указания
для выполнения лабораторных работ
Дисц.: Информатика
Киров 2011
Математический редактор MathCad
Основные сведения о MathCad
В состав Mathcad входят несколько интегрированных между собой компонентов:
· мощный текстовый редактор, позволяющий вводить, редактировать и форматировать как текст, так и математические выражения;
· вычислительный процессор, умеющий проводить расчеты по введенным формулам, используя встроенные численные методы;
· символьный процессор, позволяющий проводить аналитические вычисления и являющийся, фактически, системой искусственного интеллекта;
· огромное хранилище справочной информации, как математической, так и инженерной, оформленной в качестве интерактивной электронной книги.
Эта математическая программа удобна и практична в использовании, достаточно просто вводить математические выражения с помощью встроенного редактора формул, причем в виде, максимально приближенном к общепринятому, и тут же получать результат. Кроме того, можно изготовить на принтере печатную копию документа или создать страницу в Интернете именно в том виде, который этот документ имеет на экране компьютера при работе с Mathcad, либо можно включить документ в структуру электронной книги Mathcad.
Интерфейс Mathcad достаточно просто и понятен благодаря тому, что он сходен с интерфейсами других приложений Windows (рис. 1).
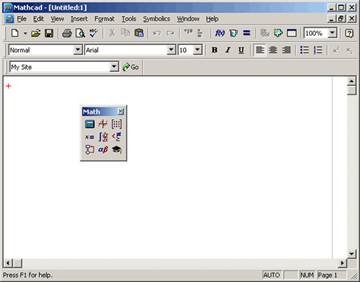
Рисунок 1 – Окно приложения MathCad с пустым документом
Помимо элементов управления, характерных для типичного текстового редактора, Mathcad снабжен дополнительными средствами для ввода и редактирования математических символов, одним из которых является панель инструментов Math (Математика) (рис. 1). С помощью этой, а также ряда вспомогательных наборных панелей удобно осуществлять ввод уравнений.
Панели инструментов служат для быстрого (в один щелчок мыши) выполнения наиболее часто применяемых команд. Все действия, которые можно выполнить с помощью панелей инструментов, доступны и через верхнее меню. На рис. 2 изображено окно Mathcad с основными панелями инструментов (три из них расположены непосредственно под строкой меню), а также дополнительными математическими (или наборными) панелями, о которых речь пойдет ниже. Основные панели:
Standard (Стандартная) — служит для выполнения большинства операций, таких как действия с файлами, редакторская правка, вставка объектов и доступ к справочным системам;
Formatting (Форматирование) — для форматирования (изменения типа и размера шрифта, выравнивания и т. п.) текста и формул;
Math (Математика) — для вставки математических символов и операторов в документы;
Resources (Ресурсы) — для быстрого вызова ресурсов Mathcad (примеров, учебников, электронных книг и т. п.);
Controls (Элементы управления) — для вставки в документы стандартных элементов управления интерфейса пользователя (флажков проверки, полей ввода и т. п.)- Эта панель на рис. 1 и 2 не показана.
Панель Math (Математика) предназначена для вызова на экран еще девяти панелей (рис. 2), с помощью которых, собственно, и происходит вставка математических операций в документы. Чтобы вызвать какую-либо из них, нужно нажать соответствующую кнопку на панели Math. Назначение математических панелей:
· Calculator (Калькулятор) — служит для вставки основных математических операций, получила свое название из-за схожести набора кнопок с кнопками типичного калькулятора;
· Graph (График) — для вставки графиков;
· Matrix (Матрица) — для вставки матриц и матричных операторов;
· Evaluation (Выражения) — для вставки операторов управления вычислениями;
· Calculus (Вычисления) — для вставки операторов интегрирования, дифференцирования, суммирования;
· Boolean (Булевы операторы) — для вставки логических (булевых) операторов;
· Programming (Программирование) — для программирования средствами Mathcad;
· Greek (Греческие символы) — для вставки греческих символов;
· Symbolic (Символика) — для вставки символьных операторов.
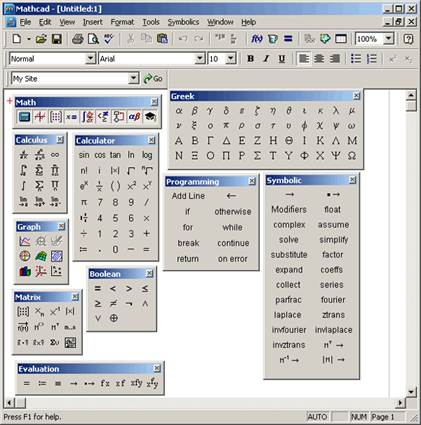
Рисунок 2 – Основные и математические панели инструментов
Вычисления в MathCad
Функции. Графики функций.
Х-У график двух векторов.
Нарисовать график функции можно двумя способами: первый, рассмотренный в предыдущем пункте, заключается во введении функции в один из местозаполнителей, а имени аргумента в местозаполнитель у другой оси. Второй заключается в дискретизации значений функции, присвоении этих значений вектору и прорисовке графика вектора.
Практическое задание!
Постройте синусоиду, сформировав два вектора данных. Данные разместите на рабочем листе в соответствии с рисунком 5. Диапазон значений i задайте при помощи команды Range Variable инструментальной панели Matrix. Индексы векторов х и у – при помощи команды Subscript этой же инструментальной панели.(для окончательного построения введите около осей имена векторов).
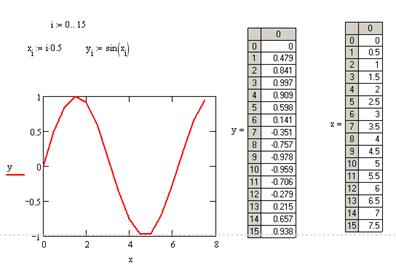
Рисунок 5 – Х-У график двух вектoров
Форматирование графиков
Возможности форматирования координатных осей графиков включают в себя управление их внешним видом/диапазоном, шкалой, нумерацией и отображением некоторых значений на осях при помощи маркеров.
Когда график создается впервые, Mathcad выбирает представленный диапазон для обеих координатных осей автоматически. Чтобы изменить этот диапазон:
1. Перейдите к редактированию графика, щелкнув в его пределах мышью.
2. График будет выделен, а вблизи каждой из осей появятся два поля с числами, обозначающими границы диапазона. Щелкните мышью в области одного из полей, чтобы редактировать соответствующую границу оси.
3. Пользуясь клавишами управления курсором и клавишами <BackSpace> и <Del>, удалите содержимое поля.
4. Введите новое значение диапазона.
5. Щелкните за пределами поля, и график будет автоматически перерисован в новых пределах.
Чтобы вернуть автоматический выбор какого-либо диапазона, удалите число из соответствующего поля и щелкните вне его. Граница шкалы будет выбрана Mathcad, исходя из значений данных, представляемых на графике.
Изменение внешнего вида шкалы, нанесенной на координатную ось, производится с помощью диалогового окна Formatting Currently Selected X-Y Plot (Форматирование выбранного графика), в котором следует перейти на вкладку X-YAxes (Оси X-Y). Вызвать диалог можно двойным щелчком мыши в области графика или выполнением команды Format / Graph / X-Y Plot (Формат / График / X-Y График) или выбором в контекстном меню команды Format (Формат).
С помощью флажков и переключателей легко поменять внешний вид каждой из осей. Перечислим доступные опции и поясним их действие:
· Log scale (Логарифмический масштаб) — график по данной оси будет нарисован в логарифмическом масштабе. Это полезно, если данные разнятся на несколько порядков;
· Grid lines (Линии сетки) — показать линии сетки;
· Numbered (Нумерация) — показать нумерацию шкалы. Если убрать этот флажок, то числа, размечающие шкалу, пропадут;
· Auto scale (Автоматический масштаб) — выбор диапазона оси производится автоматически процессором Mathcad;
· Show markers (Показать маркеры) — выделение значений на осях (см. разд. "Маркеры" далее в этой главе);
· AutoGrid (Автоматическая шкала) — разбиение шкалы производится автоматически процессором Mathcad. Если этот флажок снят, в поле ввода рядом с ним следует указать желаемое количество меток шкалы;
· Equal scales (Одинаковый масштаб) — оси х и у принудительно рисуются в одинаковом масштабе;
· Axis Style (Вид оси) — можно выбрать один из трех видов системы координат:
· Boxed (Прямоугольник) — как показано на рис. 1.25, 1.26;
· Crossed (Пересечение) — координатные оси в виде двух пересекающихся прямых;
· None (Нет) — координатные оси не показываются на графике.
Чтобы отформатировать стиль построения кривых, представляющих ряды данных, следует перейти к вкладке Trace (Кривые) диалогового окна Formatting Currently Selected X-Y Plot (Форматирование выбранного графика). На данной вкладке можно выбрать тип кривых (точки и/или линии), форму и размер маркеров точек, тип и толщину линий, а также задать цвет и легенду для каждой из кривых.
Практическое задание!
Скопируйте построенный в предыдущем упражнении график и поместите его ниже под заголовком форматирование графиков. Установите для него нумерацию шкалы и отобразите линии сетки. толщину линии сделайте 3, а цвет – любой из оттенков синего.
Трехмерные графики
Чтобы создать трехмерный график, требуется нажать кнопку с изображением любого из типов трехмерных графиков на панели инструментов Graph (График). В результате появится пустая область графика с тремя осями и единственным местозаполнителем в нижнем левом углу. В этот местозаполнитель следует ввести либо имя функции двух переменных для быстрого построения трехмерного графика, либо имя матричной переменной, которая задаст распределение данных на плоскости XY. Для получения графиков не требуется никакого текста, кроме соответствующего листинга и введения имени соответствующей функции или матрицы в местозаполнитель.
Практическое задание!
Постройте трехмерную поверхность функции 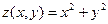 (для этого воспользуйтесь командой Surface Plot). Введите следующую матричную переменную
(для этого воспользуйтесь командой Surface Plot). Введите следующую матричную переменную  и постройте при помощи команды 3D Bar Plot трехмерную гистограмму.
и постройте при помощи команды 3D Bar Plot трехмерную гистограмму.
Алгебраические вычисления
Операторы
Арифметические операторы
Операторы, обозначающие основные арифметические действия, вводятся с панели Calculator (Калькулятор):
· сложение и вычитание: + / —;
· умножение и деление: • / * ;
· факториал: !;
· модуль числа: |х|;
· квадратный корень;
· корень n-й степени: ,
· возведение х в степень у: ху ;
· изменение приоритета: скобки;
· численный вывод: = .
Логические операторы
Результатом действия логических, или булевых, операторов являются только числа 1 (если логическое выражение, записанное с их помощью, истинно) или 0 (если логическое выражение ложно). Чтобы вычислить значение логического выражения, например 1=1 :
1. Вставьте с панели Boolean (Булевы операторы) соответствующий оператор =.
2. В появившиеся местозаполнители вставьте операнды (две единицы).
3. Нажмите клавишу <=>, чтобы получить ответ.
Логические операторы:
· больше (Greater Than) x>y;
· меньше (Less Than) x<y;
· больше или равно (Greater Than or Equal) x>_y;
· меньше или равно (Less Than or Equal) x_<y;
· равно (Equal) x=y;
· не равно (Not Equal to);
· и (And) х^у;
· или (Or) xvy;
· исключающее или (Exclusive or) x®y;
· отрицание (Not).
Практическое задание!
Выполните следующие операции сравнения: 4=5; 5=5; 6>1; 3<15; 4≤4
Матричные операторы
Матричные операторы предназначены для совершения различных действий над векторами и матрицами. Самый простой и наглядный способ создания вектора или матрицы заключается в следующем:
1. Нажмите кнопку Matrix or Vector (Матрица или вектор) на панели Matrix (Матрица), либо клавиши <Ctrl>+<M>, либо выберите пункт меню Insert / Matrix (Вставка / Матрица).
2. В диалоговом окне Insert Matrix (Вставка матрицы) задайте целое число столбцов и строк матрицы, которую хотите создать.
3. Нажмите кнопку ОК или Insert (Вставить) — в результате в документ будет вставлена заготовка матрицы с определенным числом строк и столбцов.
4. Введите значения в местозаполнители элементов матрицы. Переходить от одного элемента матрицы к другому можно с помощью указателя мыши либо клавиш со стрелками.
Добавление в уже созданную матрицу строк или столбцов производится точно так же:
1. Выделите линиями ввода элемент матрицы, правее и ниже которого будет осуществлена вставка столбцов и (или) строк.
2. Вставьте в него матрицу, как было описано выше. При этом допускается задание числа столбцов или строк равным нулю.
3. Заполните местозаполнители недостающих элементов матрицы.
Практическое задание!
Создайте матрицу А, в которой должно быть 3 строки и 2 столбца. Затем добавьте указанным выше способом еще 1 строку.
Операторы выражения
Вычислительные операторы сгруппированы на панели Evaluation:
· Численный вывод (Evaluate Numerically) = ;
· Символьный (аналитический) вывод (Evaluate Symbolically) -> ;
· Присваивание (Definition) := ;
· Глобальное присваивание (Global Definition).
3.2Алгебраические преобразования
Разложение выражений. Для этого:
1. Введите выражение cos (4х).
2. Выделите его целиком.
3. Выберите в главном меню пункты Symbolics / Expand (Символика / Разложить).
На экране появится результат разложения. При выделении части функции разложение будет производиться для выделенного фрагмента.
Упрощение выражений. Эту операцию можно произвести двумя способами. Первый аналогичен описанному выше способу разложения с той лишь разницей, что пользоваться нужно командой Symbolics/Simplify (Символика/Упростить). При втором способе нужно воспользоваться ключевым словом simplify (можно вводить его с клавиатуры или воспользоваться панелью Symbolic Keyword Toolbar.)
Разложение на множители. С помощью меню Symbolics также можно раскладывать выражения на простые множители. Для этого нужно воспользоваться командой Factor, либо ключевым словом factor панели Symbolic Keyword Toolbar.
Приведение подобных слагаемых. Эту операцию можно провести с помощью ключевого слова collect. В местозаполнителе после ключевого слова необходимо указать переменную, относительно которой требуется привести подобные слагаемые.
Разложение на простые дроби. Чтобы разложить сложную дробь на более простые дроби, следует либо выполнить команду Symbolics / Variable / Convert to Partial Fractions (Символика / Переменная / Разложить на элементарные дроби), либо указать ключевое слово parfrас. Применяя первый способ (меню), не забывайте перед выбором его команды выделить переменную, по которой будет производиться разложение, а если используется второй способ (с оператором символьного вывода), то имя переменной следует указать после ключевого слова parfrac.
Вычисление рядов и произведений. Чтобы вычислить аналитически конечную или бесконечную сумму или произведение:
1. Введите выражение, используя панель Calculus (Вычисления) для вставки соответствующих символов суммирования или произведения. При необходимости введите в качестве предела ряда символ бесконечности (клавиши <Ctrl>+<Shift>+<Z>).
2. В зависимости от желаемого стиля символьных вычислений выберите команду Symbolics / Simplify (Символика / Упростить) или введите оператор символьного вывода —>.
Вычисление пределов. Для выполнения этого действия необходимо воспользоваться панелью Calculus Toolbar, выбрав соответствующее обозначение предела.
Практическое задание! (выполняется во втором файле)
1.Разложите следующее выражение на сомножители: 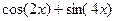 .
.
2.Упростите следующие выражения: 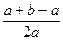 ,
, 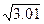 .
.
3.Разложите на простые множители следующие выражения: 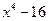 ; 28.
; 28.
4.Приведите подобные слагаемые для выражения по каждой из переменных в отдельности и одновременно для всех. 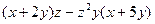 (всего должно быть проведено 4 преобразования).
(всего должно быть проведено 4 преобразования).
5.Разложите на простые дроби следующие выражения: 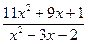 ;
; 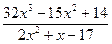 .
.
6.Вычислите следующие произведения: 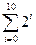 ;
; 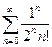 ;
; 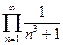 . Выражение 1 и символьно, и численно. Остальные только символьно.
. Выражение 1 и символьно, и численно. Остальные только символьно.
7. Вычислите следующие пределы: 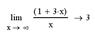 ,
, 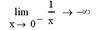 ,
, 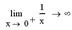 .
.
Дифференцирование
Численное дифференцирование
Для того чтобы численно продифференцировать функцию f (х) в некоторой точке, следует использовать оператор численного вывода (вместо символьного):
1. Определите точку х, в которой будет вычислена производная, например, х:=1.
2. Введите оператор дифференцирования и обычным образом введите имена функции и аргумента в местозаполнители.
3. Введите оператор = численного вывода результата.
Практическое задание!
Произведите численное дифференцирование функции 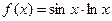 в точках х=0,1; 0,5.
в точках х=0,1; 0,5.
Производные высших порядков
Mathcad позволяет численно определять производные высших порядков, от 3-го до 5-го включительно. Чтобы вычислить производную функции f (х) N-го порядка, нужно проделать те же самые действия, что и при взятии первой производной, за тем исключением, что вместо оператора производной необходимо применить оператор м-й производной (Nth Derivative). Этот оператор вводится с той же панели Calculus (Вычисления), либо с клавиатуры нажатием клавиш <Ctrl>+<?>, и содержит еще два дополнительных местозаполнителя, в которые следует поместить число N.
Практическое задание!
Вычислите третью производную функции 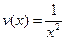 .
.
Интегрирование
Определенный интеграл
Интегрирование в Mathcad реализовано в виде вычислительного оператора. Допускается вычислять интегралы от скалярных функций в пределах интегрирования, которые также должны быть скалярными. Несмотря на то, что пределы интегрирования обязаны быть действительными, подынтегральная функция может иметь и комплексные значения, поэтому и значение интеграла может быть комплексным.
Интегрирование, как и дифференцирование, и множество других математических действий, устроено в Mathcad по принципу "как пишется, так и вводится". Чтобы вычислить определенный интеграл, следует напечатать его обычную математическую форму в документе. Делается это с помощью панели Calculus (Вычисления) нажатием кнопки со значком интеграла или вводом с клавиатуры сочетания клавиш <Shift>+<7> (или символа "&", что то же самое). Появится символ интеграла с несколькими местозаполнителями, в которые нужно ввести нижний и верхний интервалы интегрирования, подынтегральную функцию и переменную интегрирования.
Чтобы получить результат интегрирования, следует ввести знак равенства или символьного равенства. В первом случае интегрирование будет проведено численным методом, во втором — в случае успеха будет найдено точное значение интеграла с помощью символьного процессора Mathcad.
Можно вычислять интегралы с одним или обоими бесконечными пределами. Для этого на месте соответствующего предела введите символ бесконечности, воспользовавшись, например, той же самой панелью Calculus (Вычисления). Чтобы ввести (минус бесконечность), добавьте знак минус к символу бесконечности, как к обычному числу.
Подынтегральная функция может зависеть от любого количества переменных. Именно для того чтобы указать, по какой переменной Mathcad следует вычислять интеграл, и нужно вводить ее имя в соответствующий местозаполнитель. Помните, что для численного интегрирования по одной из переменных предварительно следует задать значение остальных переменных, от которых зависит подынтегральная функция и для которых вы намерены вычислить интеграл.
Практическое задание!
Вычислите определенный интеграл 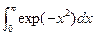 . Вычислите для этой же функции интеграл от -¥ до +¥. Вычислите интеграл
. Вычислите для этой же функции интеграл от -¥ до +¥. Вычислите интеграл 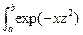 по переменным х и z.
по переменным х и z.
Неопределенный интеграл
Для того чтобы аналитически проинтегрировать некоторую функцию, следует ввести с панели Calculus (Вычисления) символ неопределенного интеграла, в появившемся в документе шаблоне заполнить местозаполнители и, наконец, ввести знак символьного равенства. В случае успеха по истечении некоторого времени расчетов справа от введенного выражения появится его аналитический результат. Если же функцию не удается проинтегрировать аналитически, введенное вами выражение будет просто продублировано.
Практическое задание!
Вычислите неопределенные интегралы: 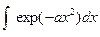 ;
; 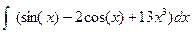
Содержание:
1 Основные сведения о MathCad. 2
2 Вычисления в MathCad. 4
2.1 Операторы численного и символьного ввода. Функции. 4
2.2 Переменные и оператор присваивания. 6
2.3 Функции. Графики функций. 7
2.3.1 Быстрое построение графика функции. Построение нескольких кривых в одной области. 7
2.3.2 Х-У график двух векторов. 8
2.3.3 Форматирование графиков. 9
2.3.4 Трехмерные графики. 11
3 Алгебраические вычисления. 11
3.1 Операторы.. 11
3.1.1 Арифметические операторы.. 11
3.1.2 Логические операторы.. 12
3.1.3 Матричные операторы.. 12
3.1.4 Операторы выражения. 13
3.2Алгебраические преобразования. 13
4 Дифференцирование. 15
4.1 Аналитическое дифференцирование. 15
4.2 Численное дифференцирование. 15
4.3 Производные высших порядков. 16
5 Интегрирование. 16
5.1 Определенный интеграл. 16
5.2 Неопределенный интеграл. 17
МАТЕМАТИЧЕСКИЙ РЕДАКТОР MathCad
Методические указания
для выполнения лабораторных работ
Дисц.: Информатика
Киров 2011
