Проверка равенства двух коэффициентов детерминации.
Другим важным направлением использования статистики Фишера является проверка гипотезы о равенстве нулю не всех коэффициентов регрессии одновременно, а только некоторой части этих коэффициентов. Данное использование статистики F позволяет оценить обоснованность исключения или добавления в уравнение регрессии некоторых наборов объясняющих переменных, что особенно ценно при совершенствовании линейной регрессионной модели.
Пусть первоначально построенное по п наблюдениям уравнение регрессии имеет вид
Y =b0+ b1X1 + b2X2 +… + bmXm
и коэффициент детерминации для этой модели равен R12. Исключим из рассмотрения k объясняющих переменных общности, положим, что это будут k последних переменных. По первоначальным n наблюдениям для оставшихся факторов построим другое уравнение регрессии:
Y =c0+ c1X1 + c2X2 +… + cm-kXm-k
для которого коэффициент детерминации равен R22. Очевидно, R22< R12, так как каждая дополнительная переменная объясняет часть (пусть незначительную) рассеивания зависимой переменной. Возникает вопрос: существенно ли ухудшилось качество описания поведения зависимой переменной Y? На него можно ответить, проверяя гипотезу H0 : R12- R22= 0 и используя статистику
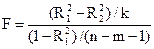
В случае справедливости H0 приведенная статистика F имеет распределение Фишера с числами степеней свободы ν1=k, ν2= n-m-1. Здесь 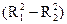 — потеря качества уравнения в результате отбрасывания k объясняющих переменных; k — число дополнительно появившихся степеней свободы;
— потеря качества уравнения в результате отбрасывания k объясняющих переменных; k — число дополнительно появившихся степеней свободы; 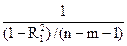 необъясненная дисперсия первоначального уравнения.
необъясненная дисперсия первоначального уравнения.
По таблицам критических точек распределения Фишера находят Fkp= Fα;k;n-m-l - требуемый уровень значимости.
Если рассчитанное значение -Fнабл статистики превосходит Fkp, то нулевая гипотеза о равенстве коэффициентов детерминации (фактически об одновременном равенстве нулю отброшенных k коэффициентов регрессии) должна быть отклонена. В этом случае одновременное исключение из рассмотрения k объясняющих переменных некорректно. Это означает, что общее качество первоначального уравнения регрессии существенно лучше качества уравнения регрессии с отброшенными переменными, так как первоначальное уравнение объясняет гораздо большую долю разброса зависимой переменной. Аналогичные рассуждения могут быть использованы и по поводу обоснованности включения новых k объясняющих переменных. В этом случае рассчитывается F-статистика:
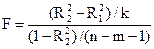
Если она превышает критическое значение, то включение новых переменных объясняет существенную часть не объясненной ранее дисперсии зависимой переменной. Поэтому такое добавление оправдано. Однако отметим, что добавлять переменные целесообразно, как правило, по одной.
Заметим, что для сравнения качества двух уравнений регрессии по коэффициенту детерминации R обязательным является требование, чтобы зависимая переменная была представлена в одной и той же форме, и число наблюдений n для обеих моделей было одинаковым.
