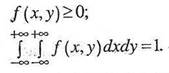Описание системы двух случайных величин.
До сих пор рассматривались случайные величины, каждое возможное значение которых определялось одним числом. Такие величины называются одномерными.
Часто результат опыта описывается не одной случайной величиной, а двумя или более случайными величинами, образующими систему. Случайные величины, возможные значения которых определяются двумя, тремя,…,пчислами, называются двумерными, трехмерными, п-мерными соответственно.
Свойства системы нескольких случайных величин не исчерпываются свойствами отдельных составляющих, они включают также взаимные связи между случайными величинами.
Рассмотрим систему двух случайных величин (X,Y), то есть двумерную случайную величину, возможные значения которой есть пары чисел (х,у).
Дискретнойназывают двумерную величину, составляющие которой дискретны.
Непрерывнойназывают двумерную величину, составляющие которой непрерывны.
Система двух случайных величин (X,Y) полностью описывается двумерным законом распределения, обычно задаваемым в одной из трех форм.
1. Ряд распределения.Для системы двух дискретных случайных величин закон распределения удобно задавать в виде прямоугольной таблицы, содержащей возможные значения и их вероятности (табл. 2.1).
Таблица 2.1
Ряд распределения системы двух дискретных величин
| X/Y | y1 | y2 | … | yj | … | yn |
| х1 | P11 | P12 | … | P1j | … | P1n |
| х2 | P21 | P22 | … | P2j | … | P2n |
| … | … | … | … | … | … | … |
| хi | Pi1 | Pi2 | … | Pij | … | Pin |
| … | … | … | … | … | … | … |
| хm | Pm1 | Pm2 | … | Pmj | … | Pmn |
Здесь Pij = P(X = хi , Y = yj) X = хi , Y = yj; i = 1,…,m; j = 1,…,n;
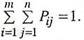
2. Функция распределения системы двух случайных величин (X,Y) – это функция F(x,y),определяющая вероятность совместного выполнения двух неравенств (X<x) и (Y<y):
F(x,y) = Р (X<x; Y<y).
Свойства функции F(x,y):
1) 0<F(x)<1.
2) Функция F(x,y) есть неубывающая функция по каждому своему аргументу:
при x2 > x1 F(x2,y) ≥ F(x1,y);
при y2 > y1 F(x,y2) ≥ F(x,y1).
3) F (x, - ∞) = F (- ∞, y) = F(- ∞, - ∞) = 0
4) F (x, + ∞) = F1(x), F ( + ∞, y) = F2(y), то есть, когда один из аргументов равен +∞,функция распределения системы превращается в функцию распределения одной случайной величины, соответствующей другому аргументу.
5)F (+ ∞, + ∞) = 1
6) Вероятность попадания случайной точки (X,Y) в прямоугольник R, ограниченный абсциссами a и b и ординатами c и d, определяется через F(x,y) по соотношению
P ( a < X < b; c < Y < d) = F(b,d) – F(b,c) – F(a,d) + F(a,c).
3. Плотность распределениясистемы двух непрерывных случайных величин есть смешанная частная производная второго порядка функции распределения:
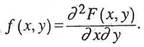
Вероятность попадания случайной точки в произвольную область Сопределяется формулой:
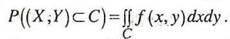
В частности, вероятность попадания случайной точки (X,Y) в прямоугольник R, ограниченный абсциссами a и b и ординатами c и d, выражается зависимостью:
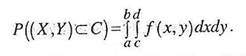
Функция распределения F(x,y) выражается через функцию плотности соотношением:
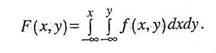
Основные свойства плотности распределения системы (X,Y):