Числовые характеристики случайных величин.

Закон распределения полностью характеризует случайную величину. Однако он часто неизвестен. В ряде случаев даже удобнее пользоваться числами, которые описывают случайную величину суммарно. Такие числа называют числовыми характеристиками случайней величины.

Рассмотрим основные числовые характеристики случайных величин.

1. Математическое ожидание случайной величины X - это ее среднее значение, которое вычисляется по формулам (для дискретной и непрерывной случайных величин соответственно):

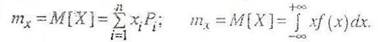
2. Модаслучайной величины (Мо) - ее наиболее вероятное значение для дискретной величины, а для непрерывной величины это то значение, при котором плотность распределения вероятностей максимальна.

3. Медиана случайной величины Х (Me) - такое ее значение Me, для которого Р(Х<Ме)=Р(Х >Me) = 0.5, то есть одинаково вероятно, окажется ли случайная величина меньше или больше Me.

3. Дисперсиейслучайной величины называется математическое ожидание квадрата разности между случайной величиной Х и ее математическим ожиданием:

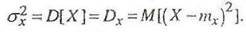
Дисперсия характеризует разброс значений случайной величины относительно ее математического ожидания. Для дискретной и непрерывной случайных величин соответственно имеем:

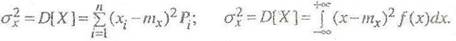
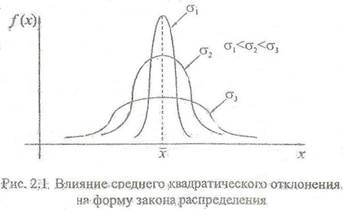
5. Средним квадратическим отклонениемслучайной величины Х называется корень из дисперсии σ_х = √D_х. Эта величинахарактеризует разброс значений случайной величины вокруг среднего значения (рис 2.1) и имеет ту же размерность, что и случайная величина.

6. Коэффициент вариации случайной величины Х характеризует относительную изменчивость величины:

K_v = σ_x / m_x

7. Начальным моментом k-го порядкаслучайной величины Х называется математическое ожидание k–й степени этой случайной величины:

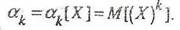
Для дискретной и непрерывной случайных величин этот момент вычисляется соответственно по формулам:

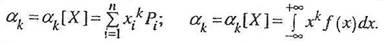
8. Центральным моментом k-го порядка случайной величины Х называется математическое ожидание k–й степени разности между случайной величиной Х и её математическим ожиданием:

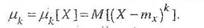
Этот момент вычисляется по следующим формулам для дискретной и непрерывной случайных величин соответственно:

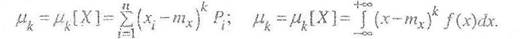
Математическое ожидание случайной величины Х есть первый начальный момент, а дисперсия – второй центральный.

Второй и третий центральные моменты выражаются через начальные моменты зависимостями:

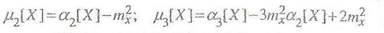
Третий центральный момент служит для характеристики асимметрии (или скошенности) распределения. Если распределение симметрично относительно математического ожидания, то все моменты нечетного порядка (если они существуют) равны нулю.

Коэффициент асимметрии (или просто асимметрия) определяется по формуле (рис 2.2):

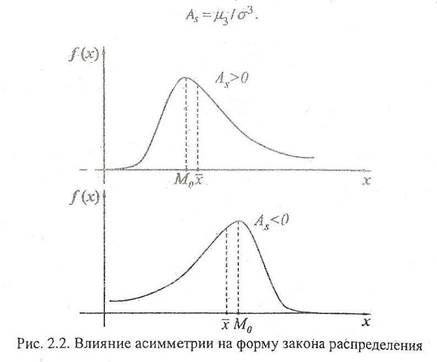
Четвертый центральный момент служит для характеристики «крутости», то есть островершинности или плосковершинности распределения.

Это свойство распределения описывается с помощью так называемого эксцесса:

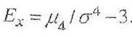
Пример. Вероятность того, что произвольный посетитель страхо­вой компании заключит с ней какой-либо договор, равна 0,4. Определить математическое, ожидание, дисперсию, среднее квадратическое отклоне­ние числа клиентов (из трех посетителей), заключивших договор со стра­ховой компанией.

Решение. Возможные значения случайной величины Х - числа клиентов (из трех посетителей), заключивших договор со страховой компанией, равны 0, 1, 2, З.

Используя формулу Бернулли, вычислим вероятности различного числа клиентов (из трех), заключивших договор со страховой компанией.

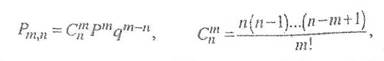
где Р = 0,4, q = 1 – P = 0,6, n = 3, m = 0,1,2,3.

Ряд распределения случайной величины Х имеет вид:

xi
Pi	0,216	0,432	0,288	0,064

Вычислим числовые характеристики величины Х.

Пример. Непрерывная случайная величина Х подчинена законy распределения с плотностью f(x) = ae^-/x/

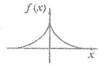
Определить математическое ожидание, дисперсию, среднее квадратическое отклонение, асимметрию, эксцесс величины X.

Решение. Определим коэффициент а.

Для этого воспользуемся свойством плотности распределения

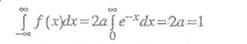
Отсюда а = 0,5.

Так как функция хe^-/x/ нечетная, то математическое ожидание величины Х равно нулю.

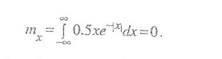
Дисперсия и среднее квадратическое отклонение, соответственно, равны:

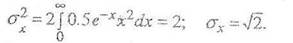
Так как распределение симметрично, то А_s = 0.

Для вычисления эксцесса находим

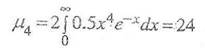
Отсюда

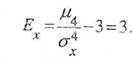
Вопросы для повторения

Что является полной количественной характеристикой описания экономического показателя как случайной величины?

Сравните различные формы законов распределения, их особенности использования.

Резюме по теме

Экономические показатели, как правило, являются случайными величинами.

Случайной величиной называется величина, которая в результате опыта (испытания) может принять одно и только одно возможное значение, заранее неизвестное и зависящее от случайных причин.

Случайные величины бывают дискретными и непрерывными.

Дискретной называют случайную величину, принимающую отдельные, изолированные друг от друга возможные значения, которые можно пронумеровать. Число возможных значений дискретной случайной величины может быть конечным или бесконечным.

Непрерывной называют случайную величину, которая может принимать все возможные значения из некоторого конечного или бесконечного промежутка.

Случайная величина полностью описывается своим законом распределения. Законом распределения случайной величины называется соотношение, устанавливающее связь между ее возможными значениями и соответствующими им вероятностями. Закон распределения может быть задан таблично (рядом распределения для дискретной величины), графически и аналитически (функцией распределения или функцией плотности распределения для непрерывной величины).