Уравнение бернулли для элементарной струйки невязкой жидкости

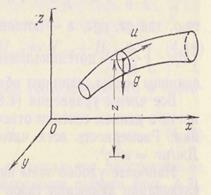Рассматривая элементарную струйку жидкости при установив­шемся движении, происходящем в поле потенциальных сил (тя­жести и давления), можно проинтегрировать уравнения (3.27) - (3.29).

В прямоугольной системе ко­ординат ориентируем плоскость хОу горизонтально, нормально к ускорению силы тяжести g (рис. 4.2). В этих условиях про­екции единичных массовых сил будут: X = 0; У = 0; Z = -g. Подставляя их значения в ура­внения (3.27)-(3.29) и учитывая, что во всех точках живого сечения элементарной струйки частицы двигаются одинаковой

скоро­стью и, получим:

Рис. 4.2. Схема к выводу

Уравнения Бернулли

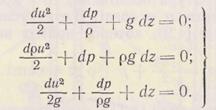(3.30)

Проинтегрируем эти выражения:

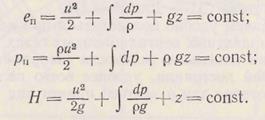(3.31)-(3.33)

Уравнения (3.31)—(3.33) являются основными при решении многих задач в гидравлике. Они представляют математическое выражение закона сохранения энергии вдоль элементарной струйки.

ЭНЕРГЕТИЧЕСКИЙ И ГИДРАВЛИЧЕСКИЙ

СМЫСЛ УРАВНЕНИЯ БЕРНУЛЛИ

Члены уравнения Бернулли выражают запас энергии, которой обладает единица массы (3.31), объема (3.32) или силы тяжести (3.33) относительно произвольно принятой горизонтальной пло­скости хОу (см. рис. 4.2). Плоскость, относительно которой со­ставляется уравнение Бернулли, называют плоскостью сравнения.

Сумма членов уравнения Бернулли дает полный запас энер­гии, которым обладает единица массы е_п, объема р_п или силы тяжести Н относительно принятой плоскости сравнения.

Члены 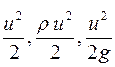выражают кинетическую энергию; суммы членов 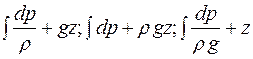- потенциальную энергию,

где gz, pgz, z - потенциальная энергия положения;

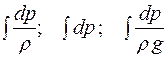I dp; - потенциальная энергия давления, соответственно единицы массы, единицы объема, единицы силы тяжести.

Все члены уравнения (3.27) выражают удельную энергию жид­кости в данном сечении относительно принятой плоскости сравнения. Размерность всех членов: L²T-², единица в системе СИ - Дж/кг = м²/с². Наиболее удобно этим видом уравнения пользоваться при ис­следовании движения газов с переменной плотностью, например в рудничных пневмосетях, компрессорах, пневмоприводах. Если при движении газа изменения давления незначительны p₂/p₁ £ 1,1 и температура постоянна, то с достаточной степенью точности можно считать r = const. В этих условиях удобно поль­зоваться уравнением (3.31), которое примет вид

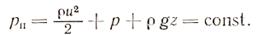(3.34)

Все члены уравнения (3.34) имеют размерность давления ML^-1 T^-2 и выражают энергию, отнесенную к единице объема. Единица р всистеме СИ — Дж/м³ = Па. Этим выражением удобно пользоваться при исследовании дви­жения воздуха в шахтных вентиляционных сетях и вентиляторах. При движении капельной жидкости (например, воды, нефти), плотность которой постоянна, удобнее всего пользоваться урав­нением (3.33), которое для р = const примет вид

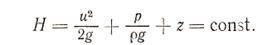(3.35)

В этом уравнении все члены имеют размерность длины L, единица Я в системе СИ — Дж/Н = м. Уравнением (3.35) широко пользуются при расчетах водопро­водов, водоотливных труб, насосов. Если взять три сечения вдоль элементарной струйки невяз­кой жидкости, то (3.35) можно записать в виде

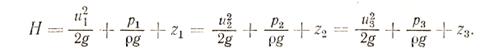(3.36)

Здесь 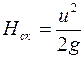- скоростной напор, определяющий кинетическую энергию;

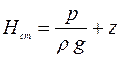- статический напор, определяющий по­тенциальную энергию.

Вводя понятие о скоростном и статическом напорах, уравне­ние (3.36) можно записать так

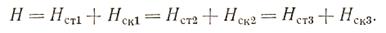(3.37)

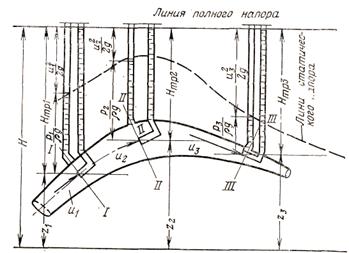
Статический напор является суммой геометрического и пьезо­метрического напоров

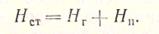(3.38)

Геометрический напор H_г = z — вертикальное расстояние от центра тяжести живого сечения до плоскости отсчета (рис. 4.3).

Рис. 4.3. Напоры в сечениях струйки невязкой жидкости

Пьезометрический напор измеряется пьезометром — трубкой, начальное сечение которой расположено нормально к вектору ско­рости.

Он определяется по формуле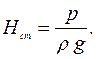

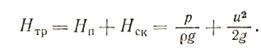
Высота подъема жидкости в трубке Пито соответствует сумме пьезометрического и скоростного напоров в точке измерения (рис. 4.3):

Зная, что 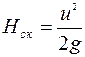, находим скорость

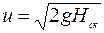(3.39)

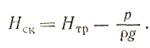
Скоростной напор измеряют как разность уровней в трубке Пито, начальный участок которой направлен против вектора скорости, и в пьезометре (рис.4.3):

Рассмотренные трубки широко применяются для определения скорости капельных жидкостей и газов. В первом случае их называют гидрометрическими, во втором пневмометрическими.

Поскольку отметка уровня жидкости в трубке Пито относительно плоскости сравнения равна полному напору Н, то во всех трубках Пито, установленных в разных сечениях вдоль струйки, уровень жидкости будет находиться на одной и той же отметке.

Линия, соединяющая уровни жидкости в скоростных трубках, называется линией полного напора, а уровни в пьезометрических трубках — линией статического или пьезометрического напора.

В этом заключается гидравлический (геометрический) смысл уравнений Бернулли. Из уравнений (3.36) и (3.37) и графиков напоров (рис.4.3) следует, что вдоль элементарной струйки невяз­кой жидкости статические и скоростные напоры могут быть раз­личными, но сумма их — полный напор Н — постоянна. Следо­вательно, линия полного напора при невязкой жидкости имеет вид прямой, параллельной плоскости сравнения.