Силы давления покоящейся жидкости на плоские стенки

Выделим на плоской боковой стенке сосуда (рис. 2.11), наклоненной в общем случае к горизонту под углом 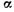, произвольную фигуру площадью F и опре­делим действующую на нее со стороны жидкости силу давления Р.

Для наглядности совместим рассматриваемую стенку с плоскостью чертежа (т. е. повернем ее на 90° вокруг оси у).

Так как давление жидкости в различных по высоте точках площади F разное, то выделим на этой площади элементарную площадку, находящуюся на расстоянии h от свободной поверхности жидкости или y=h/sina от оси х. Для такой бесконечно малой площади давление во всех ее точках одинаково и равно:

P = rgh = rgsina

следовательно, сила давления жидкости на элементарную площадку будет

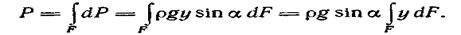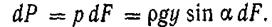
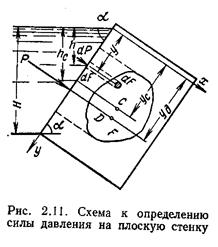
Сила давления на всю рассматриваемую площадь F

Выражение 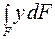представляет собой статический момент рассматриваемой площади относительно оси х, который равен произведению площади этой фигуры F на расстояние от ее центра тяжести до оси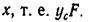

Таким образом, 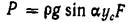или, заменяя 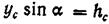,получим

Из уравнения (2.22) видно, что сила давления жидкости на плоскую стенку Р равна произведению смоченной жидкостью площади стенки F на гидростатическое давление в ее центре тя­жести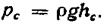

Если на свободную поверхность жидкости действует давление, отличное от атмосферного, силу давления на стенку можно найти по формулам:

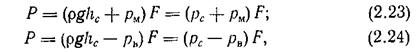
где 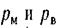- соответственно манометрическое давление и вакуум на свободной поверхности жидкости.

В ряде случаев, кроме значения силы давления жидкости на стенку, необходимо знать координаты Точки ее приложения — центра давления.

Предположим, что сила давления Р приложена в точке D, находящейся от оси х на расстоянии 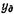. В соответствии с теоремой Вариньона о моменте равнодействующей (момент равнодействующей силы относительно какой-либо оси равен сумме моментов составляющих сил относительно той же оси)

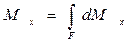или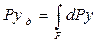

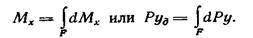Заменив в последнем выражении Р и 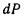их значениями, получим

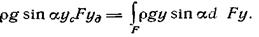Вынесем постоянные за знак интеграла и сократим их с аналогичными величинами в левой части уравнения

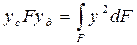
Выражение 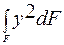представляет собой момент инерции площади фигуры относительно оси 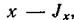который может быть выражен через момент инерции 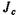относительно центральной оси, параллельной оси х, следующим образом

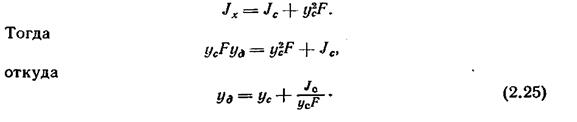
Из уравнения (2.25) видно, что центр давления для плоской стенки находится всегда ниже ее центра тяжести.

Горизонтальная координата центра давления 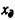находится на оси симметрии площади фигуры.

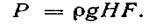
В частном случае, когда 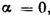, т. е. для горизонтального дна сосуда, расстояние от свободной поверхности до центра тяжести площади 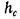будет равно высоте жидкости в сосуде Я, поэтому сила давления жидкости на дно сосуда

Из этого выражения видно, что различные по форме сосуды, имеющие одинаковые площади доньев и заполненные одинаковой жидкостью на одну и ту же высоту, будут иметь одинаковую силу давления на дно независимо от формы сосуда и количества находящейся в нем жидкости (гидростатический парадокс). Центр давления, для дна сосуда совпадает с центром тяжести площади.