Скорость и ускорение при колебательном движении

Пусть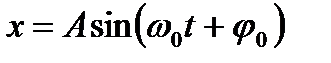

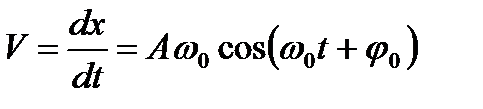-скорость, [м/с];

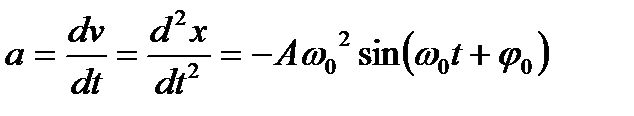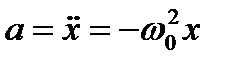или – ускорение, [м/с²].

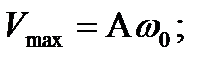
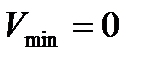
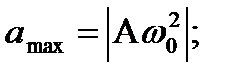
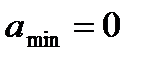
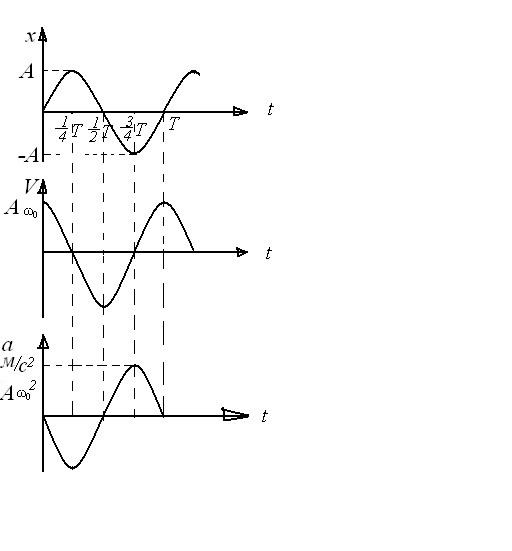
Амплитуды колебаний скорости и ускорения соответственно равны Аw₀ и Аw . Фаза колебаний скорости отличается от фазы колебаний величины отклонения на p/2, а фаза колебаний ускорения --на p. Следовательно, в моменты времени, когда х=0, dх/dt приобретает наибольшие значения; когда же s достигает максимального отрицательного значения, то d²х/dt² приобретает наибольшее положительное значение :

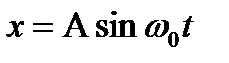
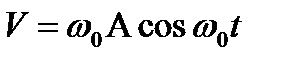
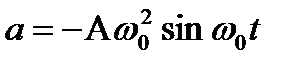
Уравнение гармонического колебания в дифференциальной форме

-

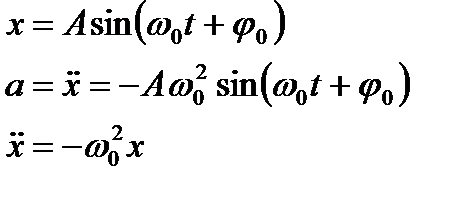Отсюда дифференциальное уравнение гармонического колебания:

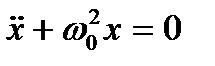или .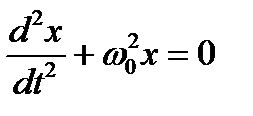

Уравнение 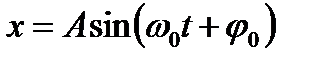является решением дифференциального уравнения.

Гармоническим колебанием называется колебание, у которого ускорение прямопропорционально смещению.

Динамика колебаний

1.Сила, действующая на колеблющуюся точку

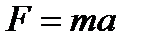
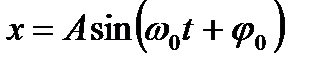,тогда

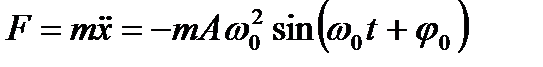или

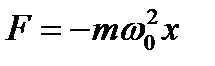- II закон Ньютона

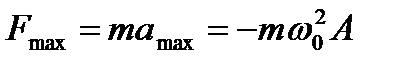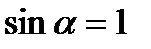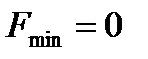(при )

(при )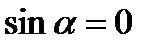

2.Кинетическая энергия

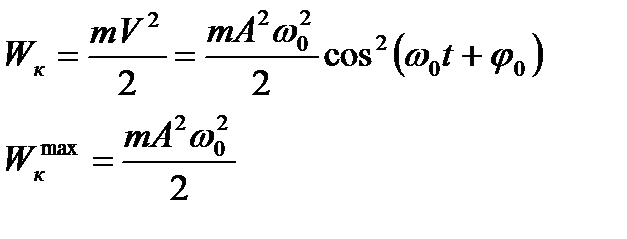
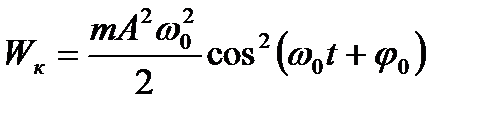
3.Полная или суммарная энергия

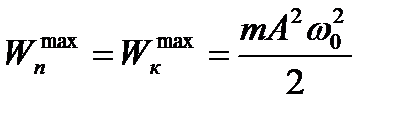
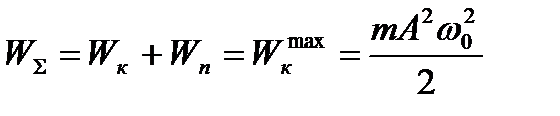
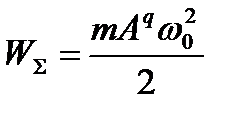
4.Потенциальная энергия

;

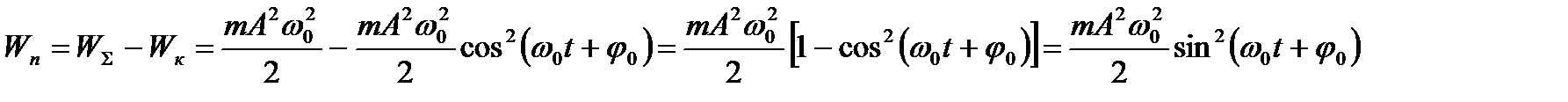
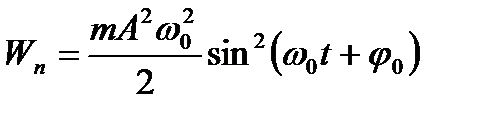Гармонический осцилятор. Маятники

Гармонический осцилятор – это система, совершающая колебания, описываемые уравнением вида

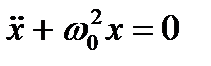
Это математическая модель периодического движения во многих задачах классической и квантовой физики.

Примером гармонического осцелятора являются пружинный, математический и физический маятники.

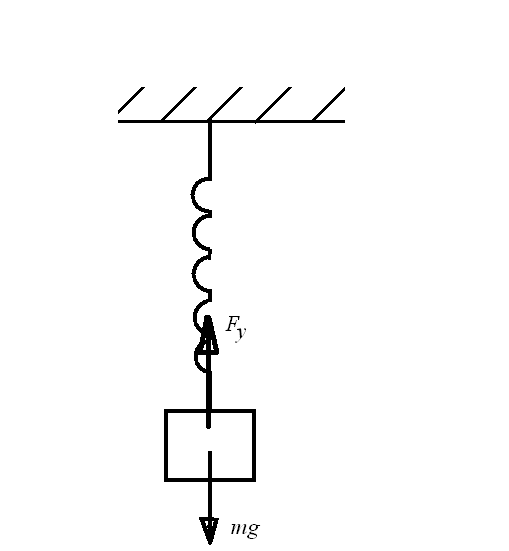1. Пружинный маятник— это груз массой т, подвешенный на абсолютно упругой пружине и совершающий гармонические колебания 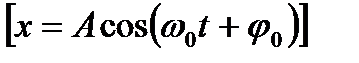под действием упругой силы F = –kx, где k —жесткость пружины.

Уравнение движения маятника

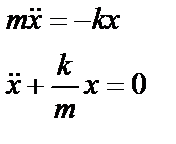
где 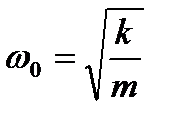циклическая частота колебаний;

Так как 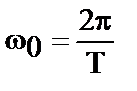, то 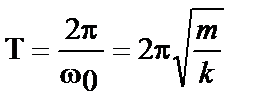- период пружинного маятника

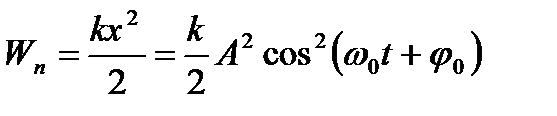- потенциальная энергия пружинного маятника

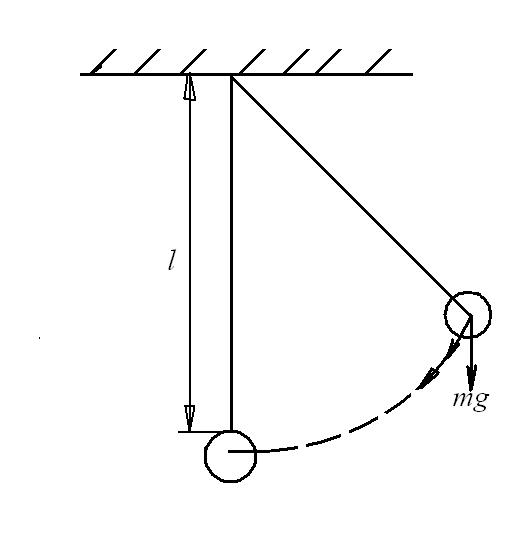2. Математический маятник

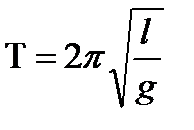период математического маятника

l – длина нити маятника

3. Физический маятник – это тело, совершающее колебания вокруг горизонтальной оси, не проходящей через центр масс С.

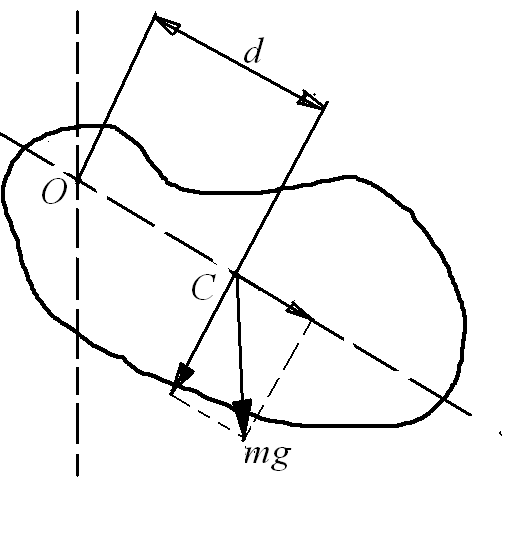d – расстояние от оси вращения до центра масс

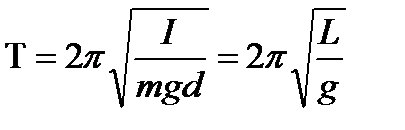
I – момент инерции тела

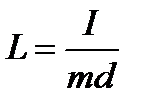- приведенная длина физического маятника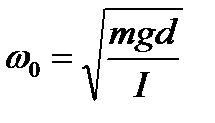

Сложение колебаний

1. Сложение одинаково направленных колебаний с одинаковой частотой методом векторных диаграмм.

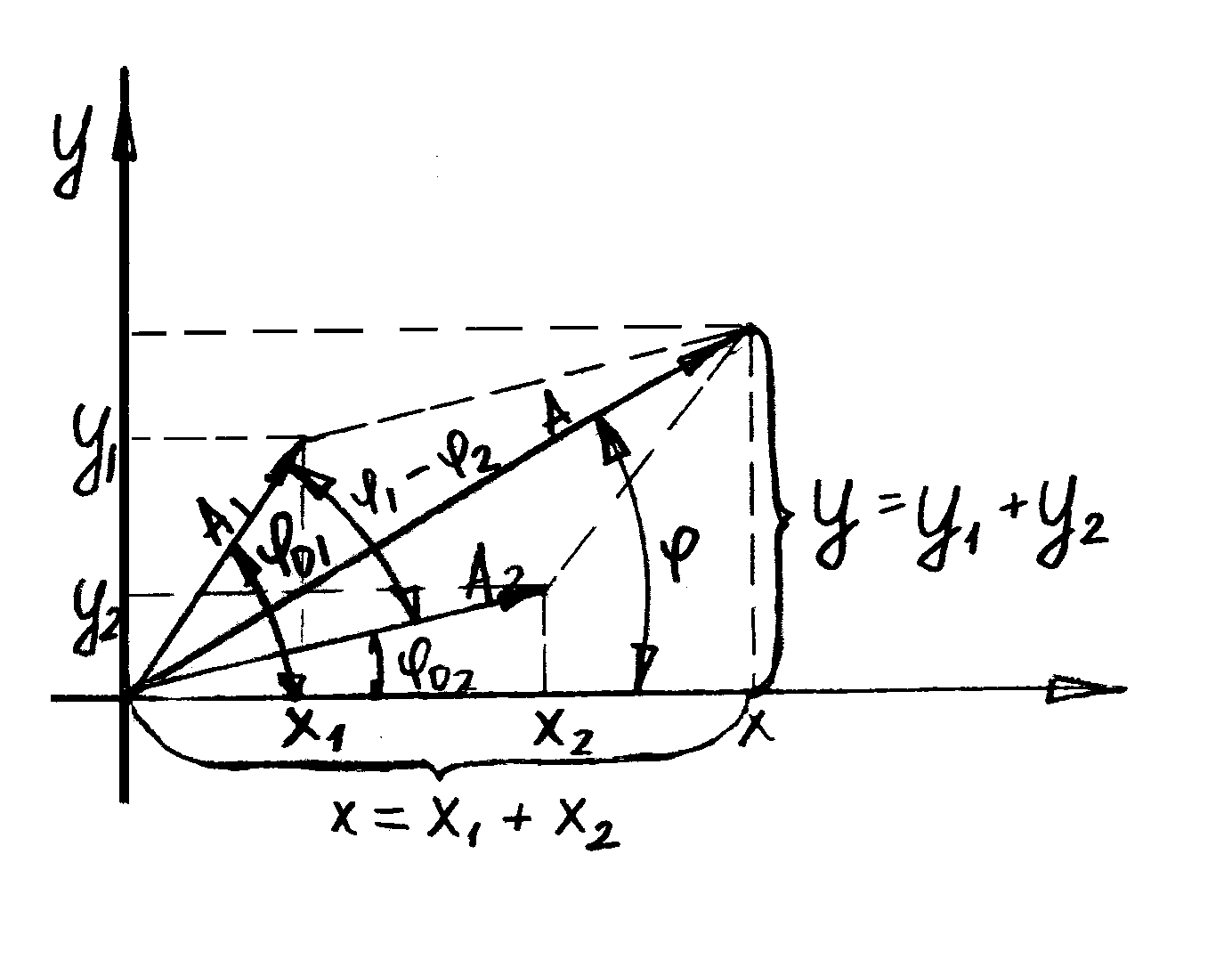
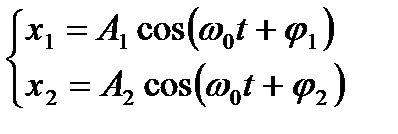
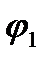-начальная фаза первого колебания.

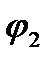-начальная фаза второго колебания.

Амплитуда результирующего колебания:

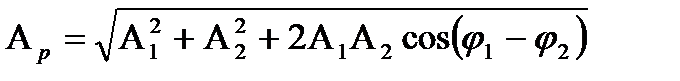
Начальную фазу результирующего колебания найдем из соотношения:

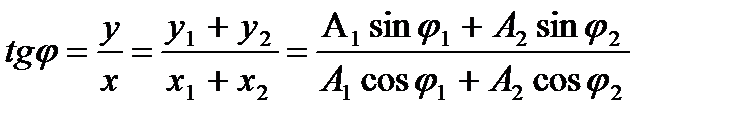
Откуда

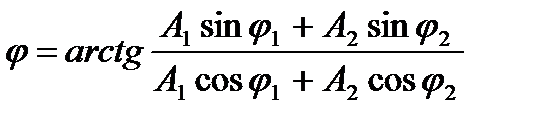
Биения.

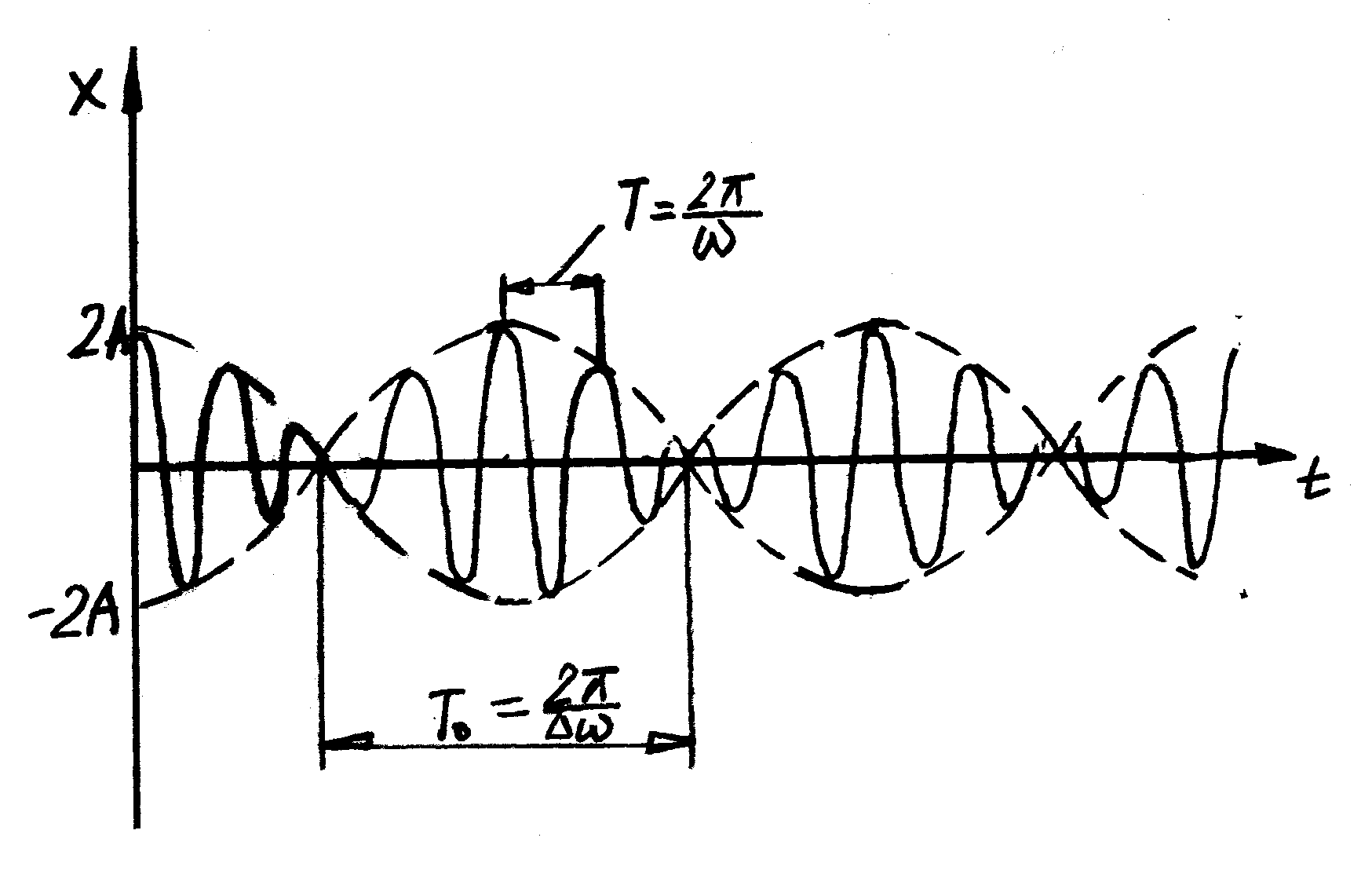
Биения возникают при складывании гармонических колебаний одинакового направления с мало отличающимися частотами. В результате сложения получаются колебания с периодически изменяющейся амплитудой.

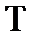- период колебаний;

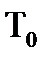- период биений.

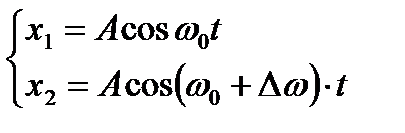Δω<<ω₀

;

;

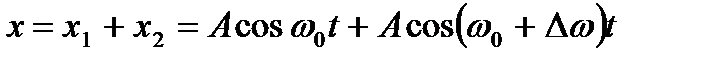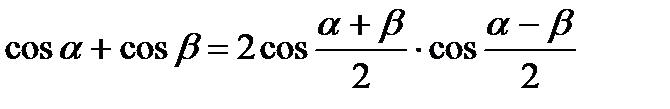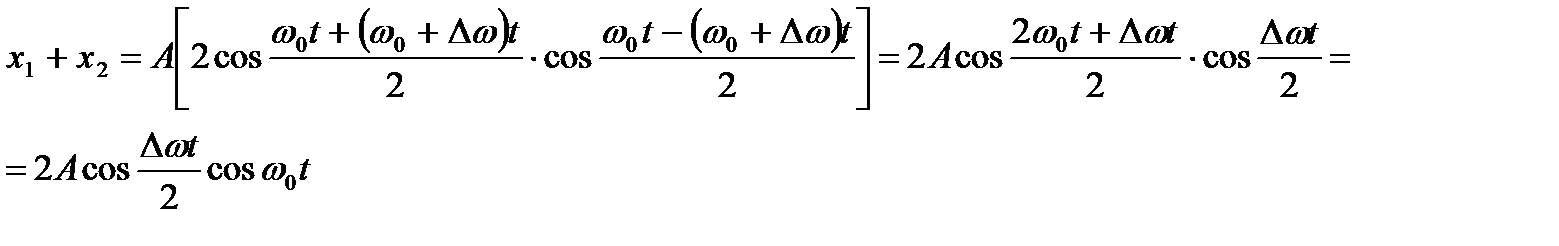
(Δω<<ω₀ → пренебрегаем)

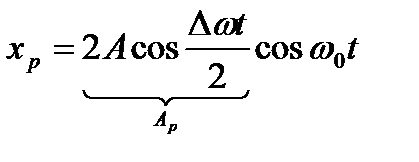
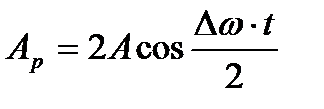- амплитуда результирующего колебания.

3. Сложение взаимно перпендикулярных колебаний. Фигуры Лиссажу

Фигура Лиссажу – это замкнутая траектория точки, которая совершает одновременно два колебания во взаимно перпендикулярных плоскостях.