Исследование модели с одной скидкой
В случае единственной скидки цена на единицу товара зависит от его объема следующим образом:
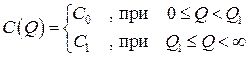
Будем называть объемом Уилсона величину  объема заказа, вычисленную по формуле Уилсона (2), т.е.
объема заказа, вычисленную по формуле Уилсона (2), т.е.
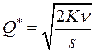
Эта формула не включает в себя закупочную цену товара и, следовательно,  едино для любой цены
едино для любой цены  .
.
При наличии только одной скидки возможны три качественно различных случая, изображенных на рис. 7 а,б,в.
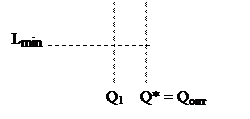
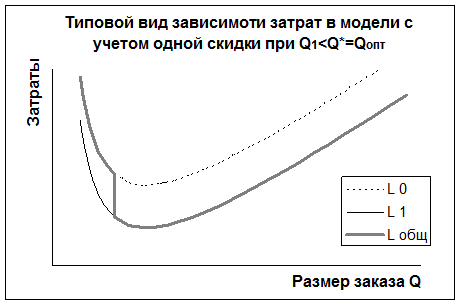

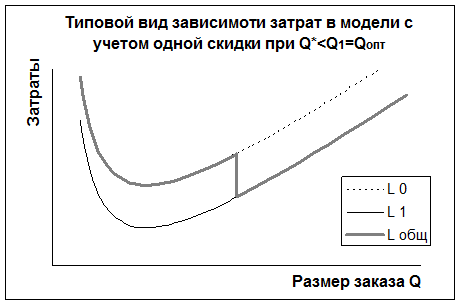
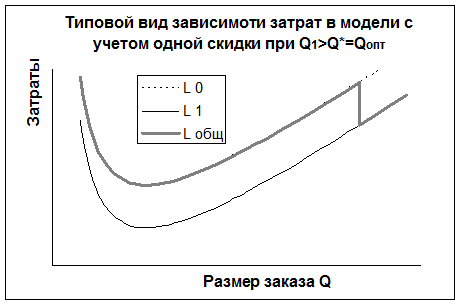
Рис. 7 а,б,в. Зависимость затрат от объема партии товара
в модели с одной скидкой
В случае, если точка разрыва цен 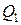 меньше или равна объему Уилсона
меньше или равна объему Уилсона  (рис. 7. а), то, очевидно, объем Уилсона является оптимальным:
(рис. 7. а), то, очевидно, объем Уилсона является оптимальным:
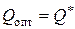 ,
,
а минимальные затраты определяются ценой со скидкой 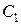 :
:
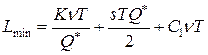
Все оптимальные параметры заказа необходимо находить по формулам (4) – (7).
В случае, если точка разрыва цен 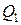 больше объема Уилсона
больше объема Уилсона  (рис. 7. б, в), то необходимо сравнить значение совокупных затрат
(рис. 7. б, в), то необходимо сравнить значение совокупных затрат 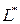 при объеме Уилсона, вычисленное по исходной цене
при объеме Уилсона, вычисленное по исходной цене 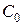 :
:
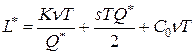
и значение совокупных затрат 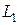 при точке разрыва цен, вычисленное при цене со скидкой
при точке разрыва цен, вычисленное при цене со скидкой 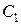 :
:
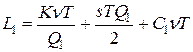 (8)
(8)
Если 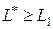 (рис. 7. б), то
(рис. 7. б), то
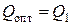
а для определения оптимальных параметров системы необходимо использовать следующие формулы:
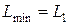
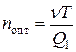
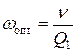
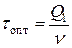
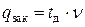
Если 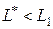 (рис. 7. в), то
(рис. 7. в), то
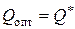 ,
,
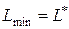 ,
,
а остальные оптимальные параметры системы определяются по формулам (4) – (7).
Исследование модели с несколькими скидками
При исследовании модели с несколькими скидками производят анализ нескольких моделей с единственной скидкой.
Сначала определяют 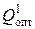 , и
, и 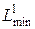 – оптимальные параметры по модели с первой скидкой относительно исходной цены, затем
– оптимальные параметры по модели с первой скидкой относительно исходной цены, затем 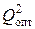 , и
, и 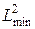 – оптимальные параметры по модели со второй скидкой относительно исходной цены и т.д. до параметров
– оптимальные параметры по модели со второй скидкой относительно исходной цены и т.д. до параметров 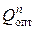 , и
, и 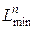 , для n-й скидки относительно исходной цены. Из всех найденных
, для n-й скидки относительно исходной цены. Из всех найденных 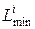 выбирают самое наименьшее:
выбирают самое наименьшее:
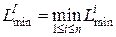
оптимальным объемом партии заказа будет 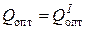 , а оптимальные параметры системы определятся по формулам:
, а оптимальные параметры системы определятся по формулам:
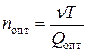 , (9)
, (9)
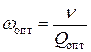 , (10)
, (10)
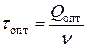 , (11)
, (11)
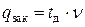 . (12)
. (12)
Пример решения задач
Задача
Объем продаж бутика составляет 96 платьев за 2 месяца. Величина спроса равномерно распределяется в течение месяца (30 дней). Цена закупки одного платья равна 2 тыс. руб. За доставку заказа владелец магазина должен заплатить 10 тыс. руб. Время доставки заказа от поставщика составляет 5 дней. Издержки хранения составляют 51 руб. в день за одно платье. Необходимо определить: сколько платьев должен заказывать владелец магазина для одной поставки, частоту заказов, точку заказа и минимальные затраты.
1. Рассмотреть случай поставок без скидок.
2. Определить оптимальные параметры работы системы управления запасов при следующих скидках:
| Размер заказа | Скидка, % | Цена, тыс. руб./шт. |
| 1–35 | Нет | |
| 36–80 | 1,8 | |
| 81 и более | 1,5 |
Следует ли владельцу магазина воспользоваться одной из скидок, предоставляемых поставщиком? Каковы при этом будут размер заказа и общие затраты на управление запасами?
Решение
Определяем входящие параметры системы.
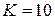 тыс. руб.;
тыс. руб.;
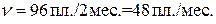 ;
;
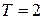 мес.;
мес.;
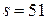 руб./пл.день. Эту величину необходимо перевести в тыс. руб./пл. мес.:
руб./пл.день. Эту величину необходимо перевести в тыс. руб./пл. мес.:
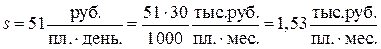 ;
;
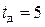 дня. Эту величину необходимо перевести в месяцы:
дня. Эту величину необходимо перевести в месяцы:
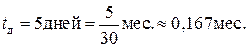
В первой части задачи:
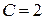 тыс. руб.
тыс. руб.
Во второй части задачи:
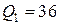 пл,
пл, 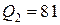 пл,
пл, 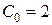 тыс. руб.,
тыс. руб., 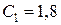 тыс. руб.,
тыс. руб., 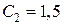 тыс. руб.,
тыс. руб.,
Решение задачи 1. Для решения первой части задачи определяем оптимальные параметры функционирования системы УЗ без скидок по формулам (2) – (7):
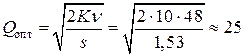 платьев.
платьев.
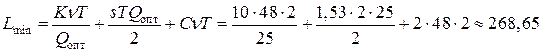 тыс. руб.
тыс. руб.
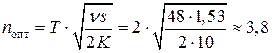 поставок за 2 месяца.
поставок за 2 месяца.
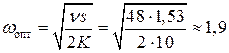 поставок в месяц.
поставок в месяц.
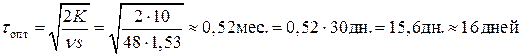 .
.
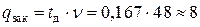 платьев.
платьев.
Вывод: при отсутствии скидок необходимо организовать поставки примерно по 25 платьев каждые 16 дней (с частотой 1,9 поставок в месяц). Заказ необходимо делать в момент, когда в наличие осталось 8 платьев. Суммарные расходы на поставку и хранение платьев составят 268,65 тыс. руб. за 2 месяца.
Решение задачи 2. Для решения задачи 2 необходимо найти  по формуле Уилсона и определить затраты без скидки при этом объеме. Это уже поделано в первой задаче:
по формуле Уилсона и определить затраты без скидки при этом объеме. Это уже поделано в первой задаче: 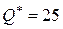 ,
, 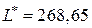 тыс. руб.
тыс. руб.
Рассмотрим сначала задачу с первой скидкой. Так как 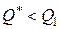 , то найдем
, то найдем 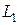 по формуле (I.4.1):
по формуле (I.4.1):
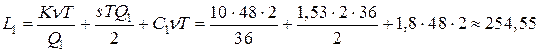 тыс. руб.
тыс. руб.
Рассмотрим теперь задачу со второй скидкой. Так как 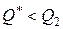 , то найдем
, то найдем 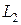 по формуле (I.4.1):
по формуле (I.4.1):
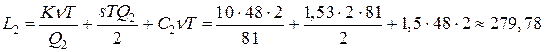 тыс. руб.
тыс. руб.
Наименьшее из значений расходов равно
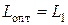 .
.
Тогда
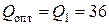 платьев.
платьев.
Остальные параметры находим по формулам (2) – (5).
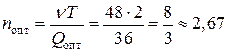 поставки за 2 мес.
поставки за 2 мес.
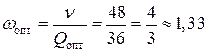 поставки в месяц.
поставки в месяц.
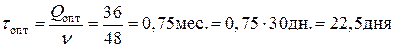
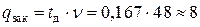 платьев.
платьев.
Вывод: при имеющейся системе скидок выгодно пользоваться первой скидкой. Необходимо организовать поставки ровно по 36 платьев примерно каждые 22 – 23 дня (с частотой 4/3 поставки в месяц). Заказ необходимо делать в момент, когда в наличие осталось 8 платьев. Суммарные расходы на поставку и хранение платьев составят примерно 254,55 тыс. руб. за 2 месяца.
Заметим, что все получившееся параметры оптимальной поставки являются примерными и могут быть скорректированы под реальную ситуацию – выходные дни, режим работы заказчика и транспортной компании и т.п. Однако число партий в заказе, равное 36, в этом случае достаточно четкая величина, обусловленная системой скидок.
Задание для самостоятельного решения
В задании данной темы:
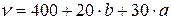 ;
;
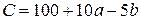 ;
;
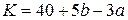 ;
;
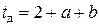 ;
;
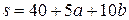 ;
;
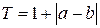 ;
;
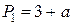 ;
;
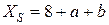 ;
;
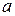 – последняя цифра номера зачетной книжки;
– последняя цифра номера зачетной книжки;
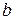 – предпоследняя цифра номера зачетной книжки.
– предпоследняя цифра номера зачетной книжки.
Объем продаж магазина «Ткани» составляет 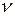 рулонов в год. Величина спроса равномерно распределяется в течение года (365 дней). Цена закупки одного рулона равна
рулонов в год. Величина спроса равномерно распределяется в течение года (365 дней). Цена закупки одного рулона равна 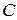 тыс. руб. За доставку и оформление заказа владелец магазина должен заплатить
тыс. руб. За доставку и оформление заказа владелец магазина должен заплатить 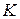 тыс. руб. Время доставки заказа от поставщика составляет
тыс. руб. Время доставки заказа от поставщика составляет 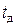 дней. Издержки хранения составляют
дней. Издержки хранения составляют 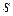 руб. в день за один рулон. Необходимо определить: сколько рулонов ткани должен заказывать владелец магазина для одной поставки, частоту заказов, точку заказа и минимальные суммарные затраты за период времени
руб. в день за один рулон. Необходимо определить: сколько рулонов ткани должен заказывать владелец магазина для одной поставки, частоту заказов, точку заказа и минимальные суммарные затраты за период времени 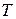 лет.
лет.
1. Рассмотреть случай поставок без скидок.
2. Определить оптимальные параметры работы системы управления запасов при следующих скидках:
| Размер заказа | Цена, тыс. руб./шт. |
От 1 до 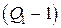 | скидки нет |
От 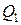 до до 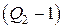 | скидка 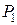 % % |
От 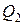 и более и более | скидка 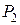 % % |
Следует ли владельцу магазина воспользоваться одной из скидок, предоставляемых поставщиком? Каковы при этом будут размер заказа и общие затраты на управление запасами?
· Записать условие задачи со своими конкретными данными.
· Выписать основные параметры и привести их к одним единицам измерения.
· Решить задачу и дать четкие ответы на все вопросы.
ТЕМА 3.
КРИТЕРИАЛЬНЫЕ МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ
Основные понятия критериальных методов
Одним из вариантов ситуации принятия решения является так называемая критериальная постановка. В этом случае лицо, принимающее решение (ЛПР), выбирает лучшие из альтернатив для достижения определенной цели. Но соответствие цели оценивается не непосредственно, а путем удовлетворения набору критериев, обладанием рядом свойств.
Наиболее известными примерами выбора решений в рассмотренной постановке являются:
· выбор автомобиля, мобильного телефона, мебели и т.п.;
· выбор сотового оператора;
· выбор места для отдыха;
· выбор варианта инвестирования средств;
· найм сотрудника;
· выбор исполнителя работ.
Невозможно назвать «лучший» автомобиль. Во-первых, важно, какую цель мы преследуем при его покупке. Но и в этом случае все неоднозначно, доказательством чему является огромное количество разных производимых и продаваемых автомобилей всех категорий. Например «лучшего автомобиля для семейного пользования» нет – кроме характеристик, следующих непосредственно из цели использования (габариты, число мест и т.п.), имеются общие характеристики (экономичность, безопасность и т.п.), характеристики экономического характера (цена, доступность на рынке и т.п.), индивидуальные предпочтения (цвет, стиль и т.п.) и другие характеристики.
В описанных ситуациях как правило можно выделить группу наиболее интересных альтернатив (подходящих по цене, удовлетворяющих большинству запросов и т.п.). Окончательный выбор из этой группы оказывается более затруднительным. Если лицо, принимающее решение, – один человек, то можно понадеяться решить проблему волевым методом. Хотя не каждому удается сделать это быстро, уверенно и без лишних психологических потрясений (как не вспомнить печальный пример Буриданова осла J). В случае же коллективного принятия решения группой лиц ситуация еще больше осложняется (вспомните выбор семейного отдыха в семье Дяди Федора из произведений Э.Успенского).
Для получения обоснованного «лучшего» решения применяют критериальные методы или методы критериального анализа иерархий.
Для названных случаев гораздо проще сравнивать альтернативы между собой не с точки зрения достижения цели, а с точки зрения удовлетворения конкретным критериям (спорное сравнение автомобилей «какой лучше для семейных поездок» превращается в более простое сравнение по цене, комфорту, экономичности, цвету и т.п.). Кроме того необходимо сравнить между собой значимость критериев для конкретной цели.
 |
Таким образом, возникает иерархичность – альтернативы обладают критериями, критерии определяют степень соответствия цели (рис. 1).
Рис. 1. Иерархическая структура ситуации принятия решения
Как правило имеются два уровня иерархии. В некоторых случаях возникают более сложные иерархии, как правило, когда критерии являются сложными, комплексными.
В 1970 г. Томас Саати (США) разработал метод анализа иерархий (Analityc hierarchy process). Кроме метода Саати существует множество других методов анализа подобных проблем. Однако именно этот метод получил широкое распространение и до сих пор активно используется в управленческой практике.
Критики метода приводят в качестве аргументов математическую неточность ряда моментов и возможность математических противоречий на этапах применения метода, отсутствие фильтрации противоречивых суждений. Однако это же является и достоинствами метода, ибо сам факт принятия решения, выбора «лучшего» и т.п. – часто противоречивая ситуация. Метод Саати приводит ЛПР не к «правильному» решению, а к варианту, наилучшим образом согласующемуся с его пониманием сути проблемы и требованиями к ее решению. Таким образом, этот метод позволяет получить объективные математические соотношения между альтернативами на основе субъективного взгляда на ситуацию лица, принимающего решение.
Метод Саати
Основа метода Саати – попарные сравнения альтернатив по каждому из критериев и попарное сравнение критериев с точки зрения важности для поставленной цели. Таким образом, все сравнения в данном методе производятся попарно, – то есть самым простым и очевидным методом. Например: какой автомобиль комфортнее, «Мерседес» или «Запорожец»?
Для сравнения Саати предложил использовать качественные признаки, переводимые потом в количественные по 9-ти балльной шкале (табл. 1).
Таблица 1.
Качественные варианты сравнения
и соответствующие им количественные баллы
| Качественное сравнение | Количественный аналог | Качественное сравнение | Количественный аналог |
| равно, одинаково, безразлично | равно, одинаково, безразлично | ||
| немного лучше, важнее | немного хуже, менее важнее | 1/3 | |
| лучше, важнее | хуже, менее важно | 1/5 | |
| значительно лучше, важнее | значительно хуже, менее важно | 1/7 | |
| принципиально лучше, важнее | принципиально хуже, менее важно | 1/9 |
Третий и четвертый столбик таблицы 1 соответствуют первому и второму для смены сравниваемых объектов. Например, если «Запорожец» принципиально лучше по критерию цена, чем «Мерседес», то «Мерседес» принципиально хуже «Запорожца» по этому критерию.
В случае, если ЛПР не может определиться между двумя качественными признаками, наличии промежуточного мнения, Саати рекомендует использовать промежуточные баллы 2, 4, 6, 8.
Определение указанных вариантов сравнения может быть осуществлено многими способами: по субъективному мнению, по экспертной оценке, путем голосования и др.
Заметим опять же субъективный подход в сравнении. Даже для критериев, имеющих четкое числовое выражение (цена, площадь и т.п.), в методике Саати нужно выбрать качественное сравнение и только потом количественное. И этому тоже есть объяснение – с качественной точки зрения соотношение между альтернативами не всегда соответствует соотношению их количественных признаков. Рассмотрим в качестве примера варианты ремонта автомобиля за счет страховых средств, ограниченных суммой 120 тыс. руб. Вся экономия остается у страховой компании, а излишки оплачиваются самостоятельно. В этом случае по критерию цена два варианта ремонта за 30 тыс. руб. и за 120 тыс. руб. практически одинаковы, а вариант за 150 тыс. руб. уже принципиально хуже.
Другим специфическим фактором является ограничение численных аналогов числом 9. Несмотря на возможность более чем 9-кратного превышения одного объекта над другим по какому-либо критерию, такой шкалы, как правило, достаточно, чтобы отразить качественное соотношение.
Запишем план или этапы применения метода Саати.
1. Выделение проблемы. Определение цели.
2. Выделение основных критериев, обуславливающих достижение цели.
3. Выделение группы альтернатив, представляющих наибольший интерес.
4. Построение иерархии: дерево от цели через критерии к альтернативам.
5. Построение матрицы попарных сравнений критериев по цели.
6. Построение матриц попарных сравнений альтернатив по критериям.
7. Применение методики анализа полученных матриц.
8. Определение весов альтернатив по системе иерархии.
Продемонстрируем применение метода Саати по пунктам плана на примере.
Пример. Организации, осуществляющей частое сопровождение договоров в другом городе, требуется купить квартиру там для проживания командированных сотрудников. Возможны поездки сотрудников разного пола. Возможно пребывание на квартире одновременно сотрудников разного ранга. Стоимость проезда по городу пребывания достаточно велика. На квартире сотрудники бывают в основном только в ночное время.
1. Выделение проблемы. Определение цели.
Цель – квартира для временного проживания сотрудников при частых командировках.
2. Выделение основных критериев, обуславливающих достижение цели.
После коллективного обсуждения на совете директоров определены следующие критерии:
· цена;
· размер;
· количество комнат;
· близость к работе;
· категория дома.
3. Выделение группы альтернатив, представляющих наибольший интерес.
После анализа предложений на рынке недвижимости выделены три наиболее интересных варианта:
· Квартира 1;
· Квартира 2;
· Квартира 3.
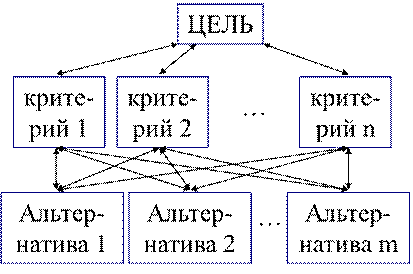
4. Построение иерархии: дерево от цели через критерии к альтернативам.
 |
Дерево иерархии представлено на рис. 2. В ряде случаев выполнение этого пункта плана не обязательно. Тем не менее, дерево иерархий дает наглядное представление ситуации принятия решения и позволяет избежать некоторых ошибок при ее анализе.
Рис. 2. Дерево иерархии для примера выбора рабочей квартиры
5. Построение матрицы попарных сравнений критериев по цели.
Путем коллективного обсуждения и, при необходимости, голосования сравниваются между собой критерии с точки зрения соответствия цели:
· цена квартиры немного важнее размера;
· цена квартиры и количество комнат одинаково важны;
· цена квартиры и близость к месту работы важны одинаково, а по некоторым мнениям цена немного менее значима;
· цена важнее категории дома;
· размер менее важен или немного менее важен, чем количество комнат;
· размер заметно менее важен, чем близость к работе;
· размер квартиры и ее категория одинаково важны или размер немного важнее;
· количество комнат и близость к работе одинаково важны;
· количество комнат важнее или даже значительно важнее, чем категория дома;
· близость квартиры к работе значительно или принципиально важнее категории дома.
Составляется таблица качественного сравнения критериев (табл. 2). сравнения взаимны, то достаточно составить только ее часть, расположенную над главной диагональю:
Таблица 2.
Качественное сравнение критериев
для примера покупки квартиры
| цена | размер | комнаты | близость | категория | |
| цена | немного важнее | одинаково важно | одинаково или немного менее важно | важнее | |
| размер | менее важно или немного менее важно | заметно менее важно | одинаково или немного более важно | ||
| комнаты | одинаково важно | важнее или значительно важнее | |||
| близость | значительно или принципиально важнее | ||||
| категория |
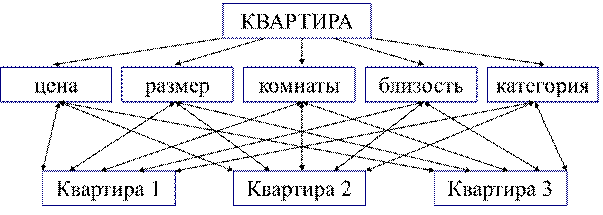
На основе таблицы качественного сравнения по таблице 1 строится таблица – матрица баллов (табл. 3). Под главной диагональю записываются числа, обратные к соответствующим числам над диагональю:  . На диагонали всегда ставятся единицы так как одинаковые критерии равны между собой:
. На диагонали всегда ставятся единицы так как одинаковые критерии равны между собой:
Таблица 3.
Количественные баллы сравнения критериев
для примера покупки квартиры
| цена | размер | комнаты | близость | категория | |
| цена | 1/2 | ||||
| размер | 1/3 | 1/4 | 1/7 | ||
| комнаты | |||||
| близость | |||||
| категория | 1/5 | 1/2 | 1/6 | 1/8 |
6. Построение матриц попарных сравнений альтернатив по критериям.
Аналогично пункту 5 строятся матрицы сравнения отдельных альтернатив по каждому из критериев.
Опустим подробное изложение всех операций и приведем ниже только матрицы количественных баллов (табл. 4 – 8):
Таблица 4.
Количественные баллы сравнения альтернатив по цене
| Квартира 1 | Квартира 2 | Квартира 3 | |
| Квартира 1 | 1/2 | ||
| Квартира 2 | 1/4 | 1/5 | |
| Квартира 3 |
Таблица 5.
Количественные баллы сравнения альтернатив по размеру
| Квартира 1 | Квартира 2 | Квартира 3 | |
| Квартира 1 | 1/2 | ||
| Квартира 2 | |||
| Квартира 3 | 1/3 | 1/4 |
Таблица 6.
Количественные баллы сравнения альтернатив по количеству комнат
| Квартира 1 | Квартира 2 | Квартира 3 | |
| Квартира 1 | |||
| Квартира 2 | |||
| Квартира 3 | 1/2 | 1/3 |
Таблица 7.
Количественные баллы сравнения альтернатив по близости к работе
| Квартира 1 | Квартира 2 | Квартира 3 | |
| Квартира 1 | 1/3 | ||
| Квартира 2 | |||
| Квартира 3 | 1/4 | 1/5 |
Таблица 8.
Количественные баллы сравнения альтернатив по категории дома
| Квартира 1 | Квартира 2 | Квартира 3 | |
| Квартира 1 | 1/5 | ||
| Квартира 2 | 1/2 | 1/6 | |
| Квартира 3 |
7. Применение методики анализа полученных матриц.
С каждой из полученных матриц применяем последовательность действий, описанных ниже. (Все действия продемонстрируем на матрице сравнения критериев. С матрицами сравнения альтернатив все операции выполняются аналогично).
7.1. Проводим нормировку матрицы:
· находим сумму элементов каждого столбца 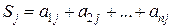 (см. табл. 9);
(см. табл. 9);
· делим все элементы матрицы на сумму элементов соответствующего столбца 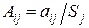 (см. табл. 10).
(см. табл. 10).
Таблица 9.
Определение сумм столбцов
| цена | размер | комнаты | близость | категория | |
| цена | 1/2=0,5 | ||||
| размер | 1/3=0,333 | 1/4=0,25 | 1/7=0,143 | ||
| комнаты | |||||
| близость | |||||
| категория | 1/5=0,2 | 1/2=0,5 | 1/6=0,167 | 1/8=0,125 | |
| СУММА | 4,533 | 15,2 | 3,417 | 2,768 |
Таблица 10.
Деление элементов на сумму соответствующего столбца
| цена | размер | комнаты | близость | категория | |
| цена | 1/4,533 = 0,221 | 3/15,2 = 0,197 | 1/3,417 = 0,293 | 0,5/2,768 = 0,181 | 5/22 = 0,227 |
| размер | 0,333/4,533 = 0,073 | 1/15,2 = 0,066 | 0,25/3,417 = 0,073 | 0,143/2,768 = 0,052 | 2/22 = 0,091 |
| комнаты | 1/4,533 = 0,221 | 4/15,2 = 0,263 | 1/3,417 = 0,293 | 1/2,768 = 0,361 | 6/22 = 0,273 |
| близость | 2/4,533 = 0,441 | 7/15,2 = 0,461 | 1/3,417 = 0,293 | 1/2,768 = 0,361 | 8/22 = 0,364 |
| категория | 0,2/4,533 = 0,044 | 0,5/15,2 = 0,013 | 0,167/3,417 = 0,049 | 0,125/2,768 = 0,045 | 1/22 = 0,045 |
7.2. Определяем веса строк. Для этого просто определяем среднее значение в каждой строке последней из полученных матриц (см. табл. 11).
Таблица 11.
Определение средних значений по строкам
| цена | размер | комнаты | близость | категория | СРЗНАЧ | |
| цена | 0,221 | 0,197 | 0,293 | 0,181 | 0,227 | 0,224 |
| размер | 0,073 | 0,066 | 0,073 | 0,052 | 0,091 | 0,071 |
| комнаты | 0,221 | 0,263 | 0,293 | 0,361 | 0,273 | 0,282 |
| близость | 0,441 | 0,461 | 0,293 | 0,361 | 0,364 | 0,384 |
| категория | 0,044 | 0,013 | 0,049 | 0,045 | 0,045 | 0,039 |
Полученный в итоге столбец задает веса строк матрицы, – в данном случае – веса критериев с точки зрения поставленной цели.
Этот столбец называют весовым столбцом критериев по цели(см. табл. 12).
Таблица 12.
Весовой столбец критериев по цели
| Вес в долях | Вес в процентах | |
| цена | 0,224 | 22,4% |
| размер | 0,071 | 7,1% |
| комнаты | 0,282 | 28,2% |
| близость | 0,384 | 38,4% |
| категория | 0,039 | 3,9% |
7.3. Промежуточные выводы.
С точки зрения удовлетворения нашей цели наиболее весомым является близость квартиры к месту работы (38,4%), далее следует количество комнат (28,2%), потом идет цена (22,4%). Размер и категория квартиры имеют наименьшие весовые коэффициенты, в сумме составляющие всего 11%.
В некоторых случаях для упрощения анализа критерии, имеющие вес ниже заданного, могут быть исключены из рассмотрения.
Действия 7.1 – 7.3 повторяем для всех матриц попарного сравнения альтернатив по критериям. Получаем следующие результаты (табл. 13 – 17):
Таблица 13.
Весовой столбец альтернатив по цене
| Вес в долях | Вес в процентах | |
| Квартира 1 | 0,334 | 33,4% |
| Квартира 2 | 0,098 | 9,8% |
| Квартира 3 | 0,568 | 56,8% |
Таблица 14.
Весовой столбец альтернатив по размеру
| Вес в долях | Вес в процентах | |
| Квартира 1 | 0,320 | 32% |
| Квартира 2 | 0,557 | 55,7% |
| Квартира 3 | 0,123 | 12,3% |
Таблица 15.
Весовой столбец альтернатив по количеству комнат
| Вес в долях | Вес в процентах | |
| Квартира 1 | 0,387 | 38,7% |
| Квартира 2 | 0,443 | 44,3% |
| Квартира 3 | 0,170 | 17% |
Таблица 16.
Весовой столбец альтернатив по близости
| Вес в долях | Вес в процентах | |
| Квартира 1 | 0,284 | 28,4% |
| Квартира 2 | 0,619 | 61,9% |
| Квартира 3 | 0,096 | 9,6% |
Таблица 17.
Весовой столбец альтернатив по категории дома
| Вес в долях | Вес в процентах | |
| Квартира 1 | 0,174 | 17,4% |
| Квартира 2 | 0,103 | 10,3% |
| Квартира 3 | 0,723 | 72,3% |
8. Определение весов альтернатив по системе иерархии.
8.1. Столбцы весов в долях альтернатив по критериям объединяем в общую матрицу весов альтернатив по всем критериям (табл. 18).
Таблица 18.
Матрица весов альтернатив по всем критериям
| цена | размер | комнаты | близость | категория | |
| Квартира 1 | 0,334 | 0,320 | 0,387 | 0,284 | 0,174 |
| Квартира 2 | 0,098 | 0,557 | 0,443 | 0,619 | 0,103 |
| Квартира 3 | 0,568 | 0,123 | 0,170 | 0,096 | 0,723 |
8.2. Умножаем полученную матрицу на столбец весов критериев по цели матрично (по правилу строка на столбец):
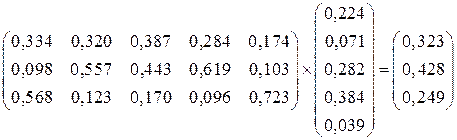
В результате получаем веса альтернатив с точки зрения достижения поставленной цели (табл. 19). Как следует из таблицы, Квартира 2 является наиболее привлекательной для поставленной цели. Если же мы будем приобретать две квартиры, то это будут квартиры 2 и 1.
Заметим, что веса альтернатив оказались достаточно близки друг к другу. Это говорит о разумном выделении всех трех квартир как объектов детального рассмотрения и анализа.
Таблица 19.
Матрица веса альтернатив
с точки зрения достижения поставленной цели
| Вес в долях | Вес в % | |
| Квартира 1 | 0,323 | 32,3% |
| Квартира 2 | 0,428 | 42,8% |
| Квартира 3 | 0,249 | 24,9% |
Важное замечание. Таблицы весовых коэффициентов критериев по цели (табл. 12) и весов альтернатив по всем критериям (табл. 18) в некоторых случаях имеют собственную ценность.
Например, в нашем случае, вектор весов критериев может использоваться многократно для разных городов. Кроме того, из него можно сделать вывод о малой важности критериев «размер» и «категория» и исключить их из рассмотрения.
В других случаях неоднократно можно использовать матрицу весов альтернатив по критериям. Примером может служить составление таблицы весов подрядчиков по критериям выполнения определенных видов работ. При получении конкретного объекта и определении важности видов работ на нем можно будет подобрать оптимального подрядчика используя же существующую таблицу.
