Критерий Гурвица (Hurwich) (пессимизма-оптимизма, компромиссный)

В этом критерии для каждой стратегии определяется «взвешенный» результат из самого пессимистического и самого оптимистического для данной стратегии. Вес каждого определяется так называемыми коэффициентами пессимизма и оптимизма, сумма которых равна единице.

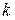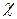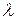Обычно в задаче задается лишь коэффициент пессимизма (или , или , или ϰ). Коэффициент оптимизма равен, соответственно, 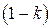. Значение этого коэффициента определяется личными особенностями лица, принимающего решения в данной ситуации и никак не зависит от вида самой матрицы.

После задания коэффициента пессимизма 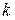и коэффициента оптимизма 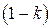для каждой стратегии находят пессимистический вариант 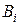и оптимистический вариант 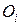и вычисляют параметр Гурвица:

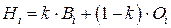
Лучшей по критерию Гурвица считается та стратегия, для которой этот результат наибольший:

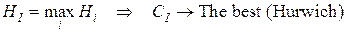
Место критерия Гурвица. Данный критерий является компромиссным между прошлыми двумя и служит для учета как лучших, так и худших вариантов стратегий.

Варианты применения критерия Гурвица. В некоторых случаях считается разумным вместо лучшего (худшего) вариантов использовать средний результат между несколькими лучшими (худшими) значениями. Встречаются случаи, когда для критерия Гурвица используют лучшее (худшее) значение, вероятность которого не меньше заданной величины. Тем самым отсекаются крайне редко реализуемые предельные значения.

Для решения задач будем использовать критерий Гурвица в классической постановке, а коэффициент пессимизма будем задавать явно в условии задачи.

Применим критерий Гурвица к нашему примеру. Коэффициент пессимизма возьмем равным 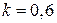. Тогда коэффициент оптимизма равен .

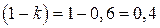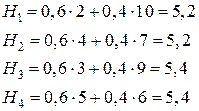
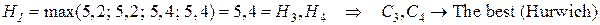
Таким образом, по критерию Гурвица наилучшими оказались две стратеги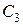и: и 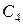, то есть по этому критерию предпочтительно привлекать научных и финансовых консультантов или только финансовых консультантов.

Критерий Сэвиджа (Savage) (минимального максимального риска)

В этом критерии сначала строится матрица (таблица) рисков. Алгоритм построения матрицы такой.

1. Матрица рисков строится по столбцам.

2. В каждом столбце находим самое большое значение выигрыша.

3. Из этого значения по очереди вычитают все значения в данном столбце и записывают результат в те же позиции.

Символьно эту процедуру можно записать в таком виде:

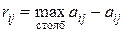
Построим матрицу рисков в нашем примере.

Максимальный элемент в первом столбце исходной матрицы равен 10. Вычитая из 10 остальные элементы столбца, получим:

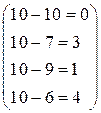, то есть первый столбец матрицы рисков равен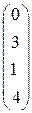

Аналогично находим элементы других столбцов:

, .

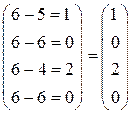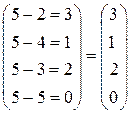Таким образом, матрица рисков для нашего примера будет иметь вид:

.

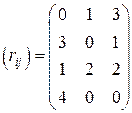Экономический смысл матрицы рисков. Элементы матрицы рисков показывают каково «недополучение» оптимальной прибыли из-за неверного выбора стратегии при данном состоянии природы.

Например, элемент «4» показывает, что если Исполнитель привлекает обоих экспертов, то в случае отсутствия проверки он недополучает 4 млн. руб. относительно максимально возможных при отсутствии проверки 10 млн. руб.

Далее в каждой строке матрицы рисков определяется наибольший результат (максимальный элемент в строке):

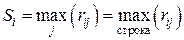
Лучшей по критерию Сэвиджа считается та стратегия, для которой этот результат наименьший:

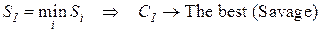
Место критерия Сэвиджа. Риск аналогичен отставанию. Таким образом, данный критерий наиболее соответствует ситуации в которой игроку важнее не отстать от конкурентов, находящихся в аналогичных условиях, нежели много выиграть или как можно меньше проиграть.

Применим критерий Сэвиджа к примеру:

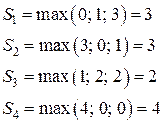
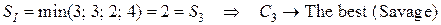
Таким образом, по критерию Сэвиджа наилучшей является стратегия 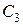, то есть при привлечении только финансовых консультантов мы рискуем потерять наименьшее значение относительно других возможных вариантов.