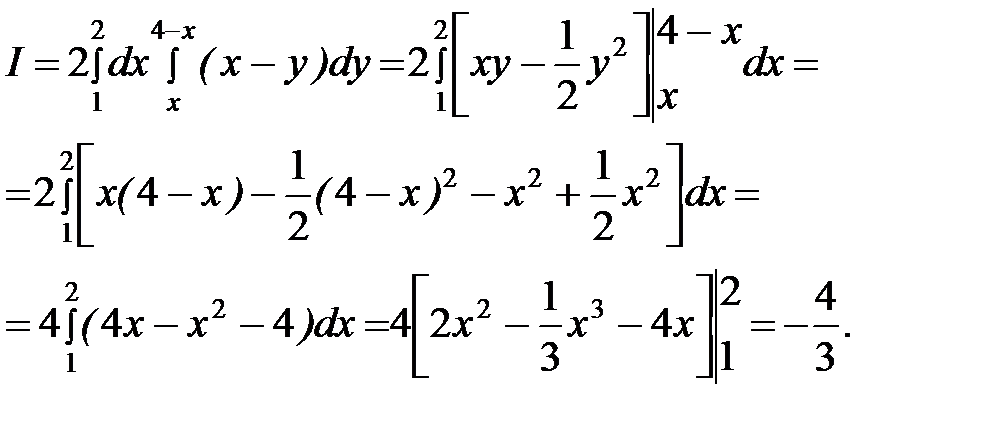Тема 2. Кратные и криволинейные интегралы

1. Знать определение двойного интеграла и его свойства.

2. Уметь вычислять повторный интеграл.

3. Уметь расставлять пределы интегрирования в двойном интеграле.

4. Уметь вычислять площадь фигур с помощью двойного интеграла.

5. Знать определение криволинейного интеграла первого рода и его свойства.

6. Уметь вычислять криволинейный интеграл первого рода.

7. Знать определение криволинейного интеграла второго рода и его свойства.

8. Уметь вычислять криволинейный интеграл второго рода.

9. Знать и уметь применять формулу Грина.

Задания для самостоятельного выполнения.

1. Вычислить повторный интеграл:

a) ;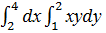

b) ;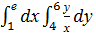

c) ;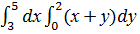

d) .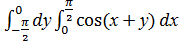

2. Расставить пределы интегрирования в том и другом порядке в повторном интеграле, к которому сводится двойной интеграл 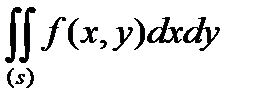, где S ограничена линиями у=х², у=4.

3. Вычислить площадь фигуры, ограниченной линиями ху=4, х+у-5=0.

4. Вычислить 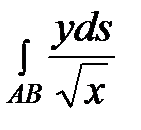, если АВ – дуга полукубической параболы 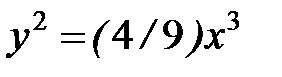от А (3, 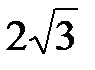) до В (4; 2).

5. Вычислить криволинейный интеграл 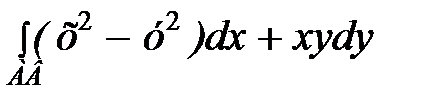, если путь от А(1; 1) до В (3; 4) – отрезок прямой.

Образцы решения заданий.

Задание 1. Расставить пределы интегрирования в двойном интеграле 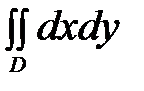в том и другом порядке, если область 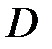задана линиями 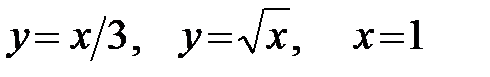и вычислить площадь этой области.

Решение. Строим область :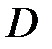

x

1/3

y

y=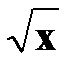

y=x/3

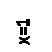Рисунок 1– Область D

Площадь плоской области 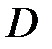с помощью двойного интеграла вычисляется по формуле

.

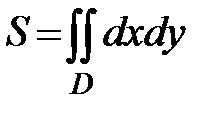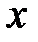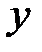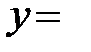
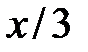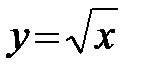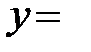
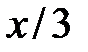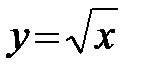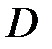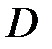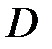Расставим пределы интегрирования в том и другом порядке. Переменная изменяется от 0 до 1, в это время изменяется от прямой до параболы , так как прямая, параллельная оси ОУ, пересекает сначала прямую (нижний предел), а затем параболу (верхний предел). При изменении порядка интегрирования область придется разбить на две области ₁ и ₂ прямой, параллельной оси 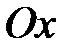, так как правая часть контура области 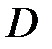состоит из двух линий, определяемых разными уравнениям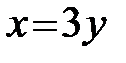и и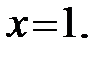

Следовательно,

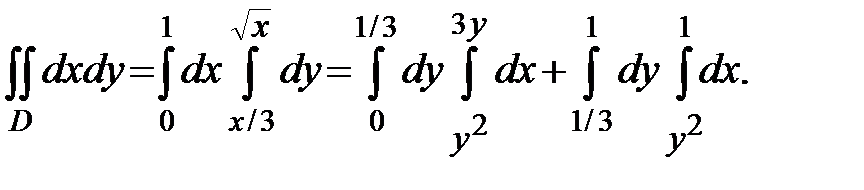
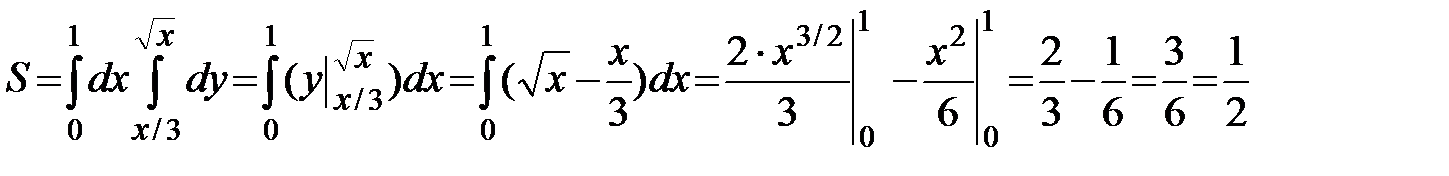( кв.ед.)

Задание 2.Сделать чертеж области интегрирования. Изменить порядок интегрирования в двойном интеграле I = 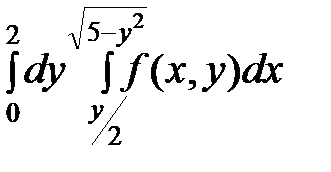и вычислить в одном из случаев двойной интеграл при .

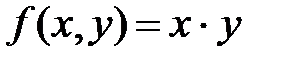Решение.Зная пределы интегрирования 0 ≤ у ≤ 2, 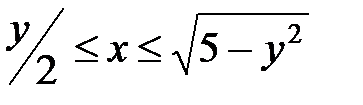, найдем границы области интегрирования D: у = 0, у = 2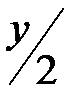, х = , х = 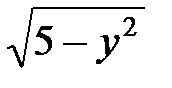и построим их (рисунок 2).

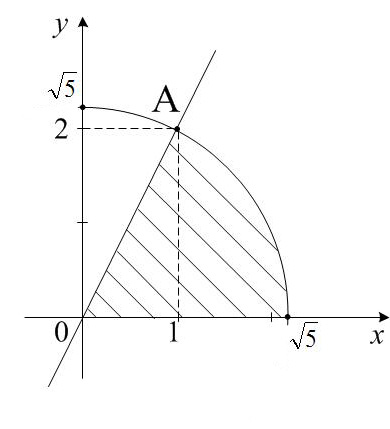
Рисунок 2 – Область интегрирования

Найдем координаты точки А, точки пересечения прямой х = 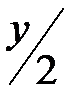и полуокружности х = 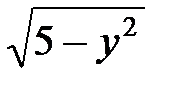. Так как в точке пересечения ордината у = 2, то подставив в любое из двух уравнений, найдем х = 1. Итак, точка А имеет координаты А(1;2).

Для того чтобы расставить пределы интегрирования в другом порядке, проведем через область D прямые, параллельные оси Оу. Эти прямые пересекают сначала ось Ох, затем прямую у = 2х или дугу полуокружности у = 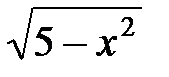. Следовательно, линией входа будет у = 0 (0 ≤ х ≤ 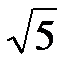), а линиями выхода будут у = 2х (0 ≤ х ≤ 1) и у = 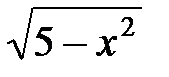(1 ≤ х ≤ 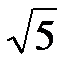). Так как линия выхода задается двумя различными аналитическими выражениями, то область D необходимо разбить прямой х = 1 на две области, и двойной интеграл будет равен сумме интегралов по каждой из этих областей.

Таким образом, получим

I .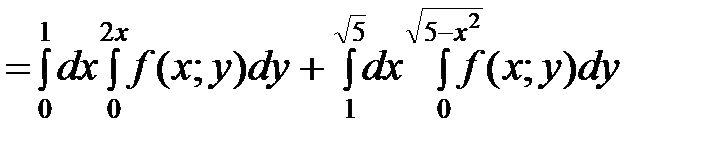

Вычислим I = 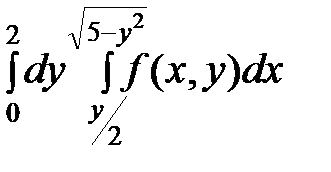,если 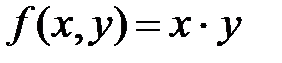,то есть

I = .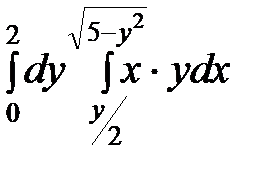

Вычисляем сначала внутренний интеграл по переменной х, считая у постоянной величиной, имеем:

I= = = =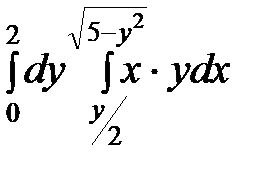

= = =

= = = .

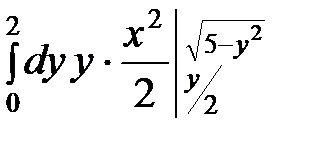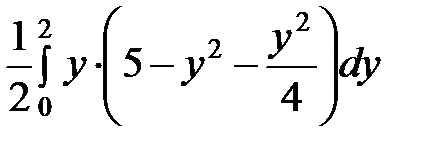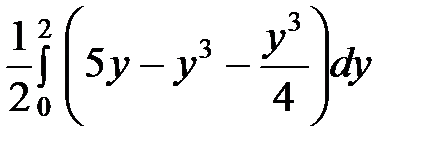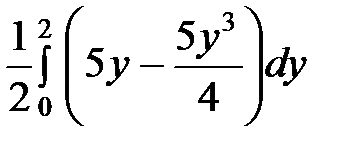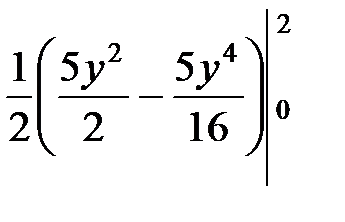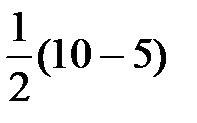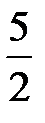Ответ: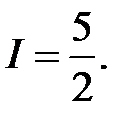

Задание 3.Вычислить 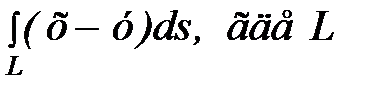– отрезок прямой от А(0; 0) до В (4; 3).

Решение.Уравнение прямой АВ имеет вид 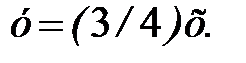Находим 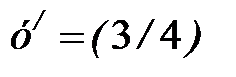и, следовательно,

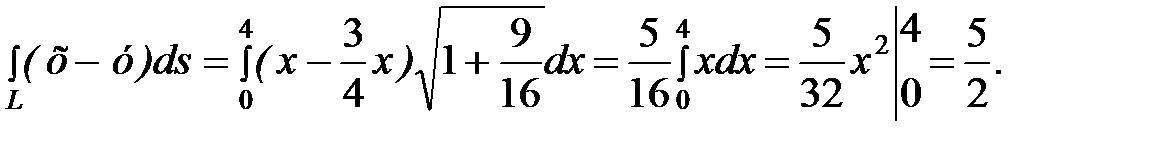
Задание 4. Вычислить криволинейный интеграл ,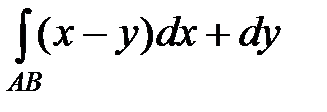

где АВ–дуга параболы 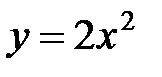от т.А( 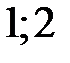) до т.В ( ).

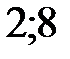Решение. Изобразим кривую, вдоль которой ведется интегрирование:

Рисунок 3 – Кривая, вдоль которой ведется интегрирование

Вычисление криволинейного интеграла 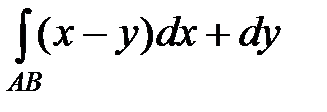сведем к вычислению определенного интеграла по формуле

= .

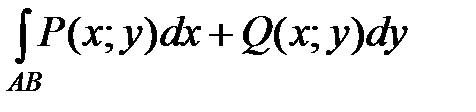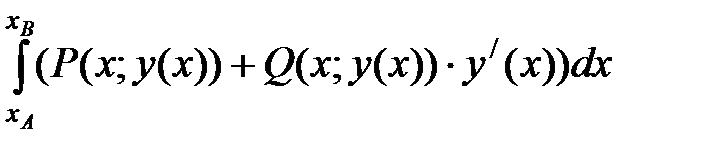Так как АВ–дуга параболы, заданной уравнением 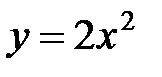от т.А( 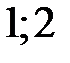) до т.В ( 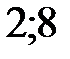), то 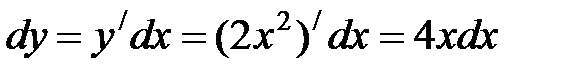, а переменная 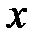меняется в пределах от 1 до 2. Следовательно,

= = =

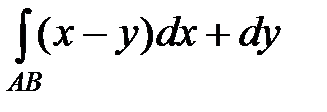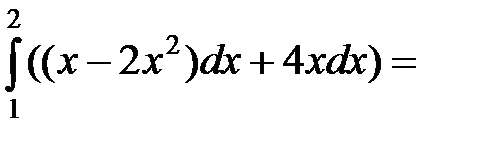
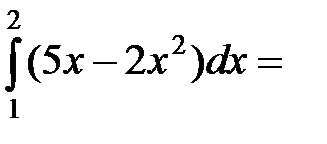
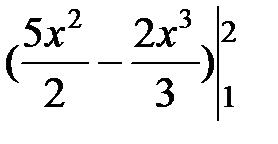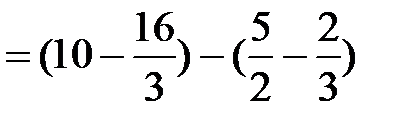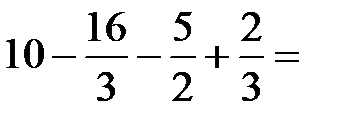
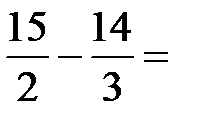
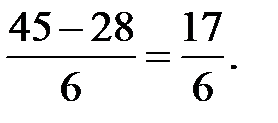
Задание 5. Применяя формулу Грина, вычислить 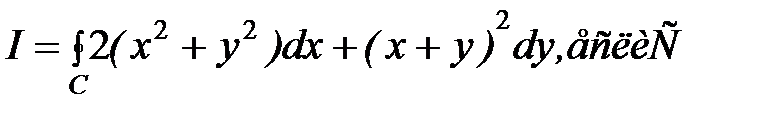– контур треугольника с вершинами L(1; 1), М(2; 2), N(1; 3), пробегаемый против хода часовой стрелки.

Решение. Здесь 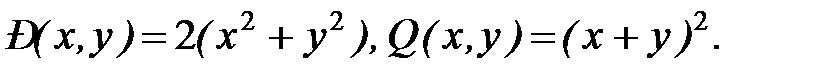Находим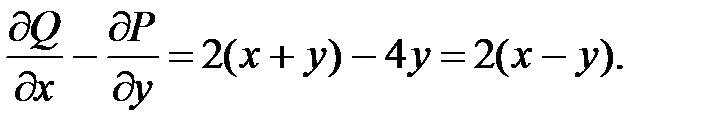

Таким образом,

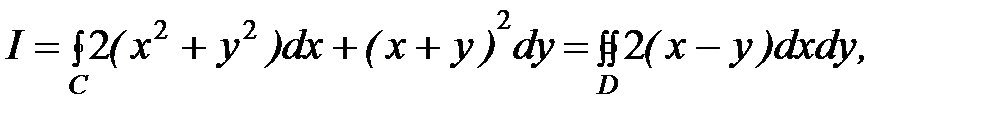где область D– треугольник LMN.Уравнение прямой LM: y=x, уравнение MN: y=–x+4.Вычислим двойной интеграл по данной области: