Дифференциальное исчисление функции двух переменных

Функция двух переменных

Если каждой паре действительных чисел (x; y) из области D по определенному правилу ставится в соответствие только одно число z из области Е, то говорит, что на множестве D задана функция двух переменных

z = z(x, y).

Значение z(a; b) функции z = z (x, y) есть значение этой функции, вычисленное при x = a, y = b.

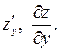Частной производной функции z = z(x, y) по аргументу x называется производная этой функции по x, при постоянномy.

Обозначения:

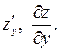Аналогично, частной производной функции z = z(x, y) по аргументу y называется производная этой функции по y при постоянномx.

Обозначения:

При дифференцировании полезна следующая таблица:

Х/Х=1	Х/У=0
У/У=1	У/Х=0
С/Х=0	С/У=0	С - const

Задача :Найти частные производные функции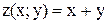

Решение: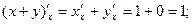

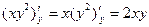
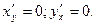
Задача. Найти частные производные функции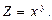

Решение: Найдем производную функции Z по переменной x. В этом случае, при дифференцировании величина y считается постоянной и поэтому: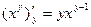

Аналогично найдем производную функции по y, считая величину x постоянной: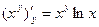

Задача. Найти частные производные z_x', z_y'для функции

z =x³–3x²y+2y³+1,

Решение:

z_x' =(x³–3x²y+2y³+1)_x' =(x³)_x'–(3x²y)_x' +(2y³)_x'+1_x' =3x² -3y(x²)_x' +0+0=3x²–6xy

z_y'=(x³–3x²y+2y³ +1)_y' = (x³)_y'–(3x²y)_y+(2y³)_y'+1_y'=0–3x²y_y'+2(y³)_y'+0=-3x²+6y²

Задача . 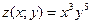. Найти 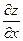и .

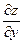При вычислении частной производной по переменной x заметим, что 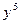является постоянной величиной, а постоянный множитель можно выносить за знак производной. Поэтому имеем

.

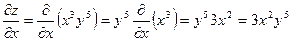Аналогично, при вычислении частной производной по переменной y заметим, что 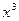является постоянной величиной, а постоянный множитель можно выносить за знак производной. Поэтому имеем

.

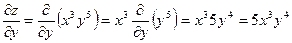Задача. 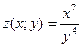. Найт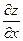и и .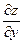

Решение: При вычислении частной производной по x заметим, что 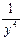является постоянным множителем. Тогда

.

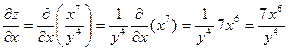Аналогично при вычислении частной производной по y заметим, что 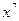является постоянным множителем. Тогда

.

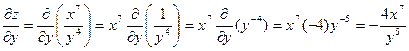Частными производными второго порядка функции z=z(x, y) называются частные производные от частных производных первого порядка.

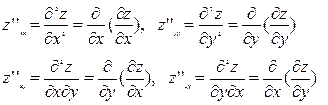Порядок дифференцирования указан в индексе при прочтении слева направо.

Последние две производные отличаются только порядком, называются смешанными и в случае их непрерывности равны.

Задача: Найти все частные производные 2-ого порядка и проверить равенство z¢¢_xy=z¢¢_yxдля функции z=x²-2xy²

Решение: Вначале найдем частные производные первого порядка:

z¢_x=(x²-2xy²)¢_x=2x-2y², z¢_y= (x²-2xy²)¢_y=-4xy

Далее частные производные второго порядка:

z¢¢_xx= (2x-2y²)¢_x= 2, z¢¢_yy= (-4xy)¢_y = -4x

z¢¢_xy= (2x-2y²)¢_y= -4y, z¢¢_yx= (-4xy)¢_x = -4y

Нетрудно видеть, что z¢¢_xy = z¢¢_yx

Выполнение этого условия может служить критерием правильности нахождения частных производных 1-огопорядка и смешанных – 2-ого порядка.

Производная сложной функции

Если z=z(u,v), где u=u(x,y), v=v(x,y), то частная производная функции zпо переменной xи частная производная функции zпо переменной yсоответственно равны:

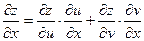
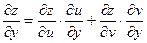
Задача: Найт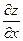и и 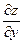, если 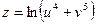, где , .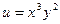

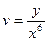Решение:

.

.

.

.

.

.

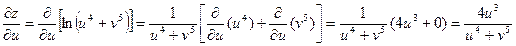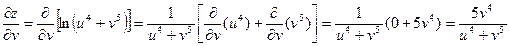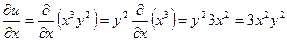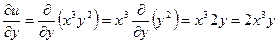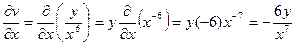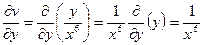Тогда

= + .

= + .

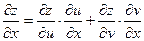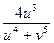
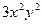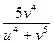
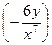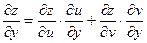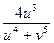
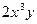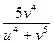
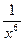Задача. Найти частные производные второго порядка от функции .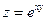

Решение: Сначала найдем частные производные первого порядка:

; .

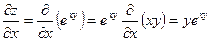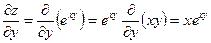Дифференцируя по переменным x и y полученные частные производные 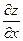и 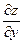, получим:

;

.

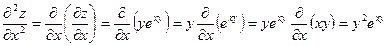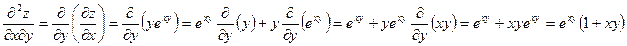
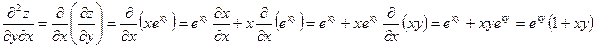
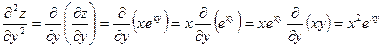Мы получили, что 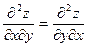. Это совпадение не является случайным. Имеет место важная теорема: Если частные производные (всех порядков) функции непрерывны, то их значения не зависят от порядка дифференцирования.