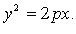Формула для вычисления угла между плоскостями

Если заданы уравнения плоскостей A₁x + B₁y + C₁z + D₁ = 0 и A₂x + B₂y + C₂z + D₂ = 0, то угол между плоскостями можно найти, используя следующую формулу

cos α =	|A1·A2 + B1·B2 + C1·C2|
√A12 + B12 + C12√A22 + B22 + C22

2) Условия перпендикулярности 2х плоскостей. Ясно, что две плоскости перпендикулярны тогда и только тогда, когда их нормальные векторы перпендикулярны, а следовательно, 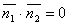или .

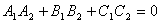Таким образом, .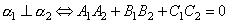

3) Условия параллельности 2х плоскостей.Две плоскости α₁ и α₂ параллельны тогда и только тогда, когда их нормальные векторы 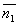и 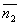параллельны, а значит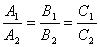

32 вопрос.

Уравнение прямой в пространстве. Различные способы задания прямой в пространстве. Угол между плоскостям. Взаимное расположение прямых и плоскостей.

1)Уравнение прямой на плоскости в прямоугольной системе координат O(x;y)представляет собой линейное уравнение с двумя переменными x и y, которому удовлетворяют координаты любой точки прямой и не удовлетворяют координаты никаких других точек. С прямой в трехмерном пространстве дело обстоит немного иначе – не существует линейного уравнения с тремя переменными x, y и z, которому бы удовлетворяли только координаты точек прямой, заданной в прямоугольной системе координат O(x;y;z). Действительно, уравнение вида 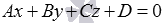, где x, y и z – переменные, а A, B, C и D – некоторые действительные числа, причем А, В и Содновременно не равны нулю, представляет собой общее уравнение плоскости. Тогда встает вопрос: «Каким же образом можно описать прямую линию в прямоугольной системе координат O(x;y;z)

2)Если в трехмерном пространстве введена прямоугольная система координат и задана прямая с помощью указания координат двух ее точек, то мы имеем возможность составить уравнение прямой, проходящей через две заданные точки.

Второй способ задания прямой в пространстве основан на теореме: через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и причем только одна.

Следующий способ задания прямой в пространстве основан на аксиоме стереометрии: если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.

Таким образом, задав две пересекающиеся плоскости, мы однозначно определим прямую в пространстве.

Смотрите также статью уравнения прямой в пространстве - уравнения двух пересекающихся плоскостей.

Способ задания прямой в пространстве следует из теоремы (ее доказательство Вы можете найти в книгах, указанных в конце этой статьи): если задана плоскость и не лежащая в ней точка, то существует единственная прямая, проходящая через эту точку и перпендикулярная к заданной плоскости.

Таким образом, чтобы определить прямую, можно задать плоскость, которой искомая прямая перпендикулярна, и точку, через которую эта прямая проходит.

Если прямая задана таким способом относительно введенной прямоугольной системы координат, то будет полезно владеть материалом статьи уравнения прямой, проходящей через заданную точку перпендикулярно к заданной плоскости.

3)Во-первых, две прямые могут совпадать, то есть, иметь бесконечно много общих точек (по крайней мере две общие точки).

Во-вторых, две прямые в пространстве могут пересекаться, то есть, иметь одну общую точку. В этом случае эти две прямые лежат в некоторой плоскости трехмерного пространства. Если две прямые в пространстве пересекаются, то мы приходим к понятию угла между пересекающимися прямыми.

В-третьих, две прямые в пространстве могут быть параллельными. В этом случае они лежат в одной плоскости и не имеют общих точек. Рекомендуем к изучению статью параллельные прямые, параллельность прямых.

Две прямые в трехмерном пространстве могут быть скрещивающимися. Две прямые в пространстве называются скрещивающимися, если они не лежат в одной плоскости. Такое взаимное расположение двух прямых в пространстве приводит нас к понятию угла между скрещивающимися прямыми.

Особое практическое значение имеет случай, когда угол между пересекающимися или скрещивающимися прямыми в трехмерном пространстве равен девяноста градусам. Такие прямые называют перпендикулярными (смотрите статью перпендикулярные прямые, перпендикулярность прямых).

41.

42.

43.

44.

45.

46.

Гипербола. Ее уравнение.

Гиперболой называется множество точек плоскости, разность расстояний от каждой из которых до двух заданных (называемых фокусами) есть величина постоянная. Эта постоянная величина положительна и меньше расстояния между фокусами.

Фокусы гиперболы обозначаются буквами 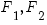, расстояние между фокусами – через 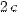, постоянную разность между расстояниями от любой точки гиперболы до ее фокусов – через 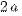(2a<2с).

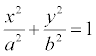
Окружность. Ее уравнение.

Окружность — замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра), лежащей в той же плоскости, что и кривая.

В уравнение окружности (x – a)² + (y – b)² = R², где (a; b) — координаты центра, а R — радиус окружности.

Пример 1. Найти координаты центра и радиус окружности, если ее уравнение задано в виде: 2x² + 2y² – 8x + 5y – 4 = 0.

Решение:

Для нахождения координат центра и радиуса окружности данное уравнение необходимо привести к виду, указанному выше в п.9. Для этого выделим полные квадраты: x² + y² – 4x + 2,5y – 2 = 0;

x² – 4x + 4 –4 + y² + 2,5y + 25/16 – 25/16 – 2 = 0; (x – 2)² + (y + 5/4)² – 25/16 – 6 = 0;

(x – 2)² + (y + 5/4)² = 121/16. Отсюда находим О(2; -5/4); R = 11/4.

Фокусы эллипса.

Эллипс-это геометрическая фигура, которая ограничена кривой, заданной уравнением .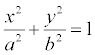

Определение.Он имеет два фокуса. Фокусаминазываются такие две точки, сумма расстояний от которых до любой точки эллипса есть постоянная величина.

Чертеж фигуры эллипс

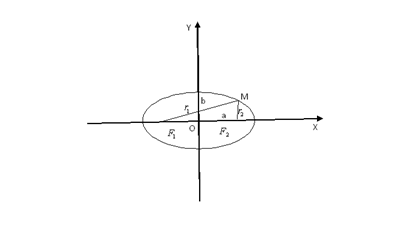
F₁ , F₂ – фокусы . F₁ = ( c ; 0); F ₂ (- c ; 0)

с – половина расстояния между фокусами;

a – большая полуось;

b – малая полуось.

Теорема.Фокусное расстояние и полуоси связаны соотношением:

a² = b ² + c ².

Пример 2.Составить каноническое уравнение эллипса, у которого большая ось равна 10, координаты фокусов 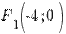и .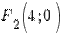

Решение. Фокусы эллипса расположены на оси 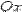. Имеем, 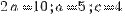.Из соотношения 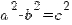находим 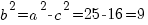,т.е. 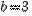.Итак, каноническое уравнение эллипса имеет вид :

44. Соотношение осей и расстояний эллипса.

Теорема. Фокусное расстояние и полуоси эллипса связаны соотношением:

A2 = B2 + C2.

Доказательство: В случае, если точка М находится на пересечении эллипса с вертикальной осью, R1 + R2 = 2 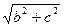(по теореме Пифагора). В случае, если точка М находится на пересечении эллипса с горизонтальной осью, R1 + R2 = A – C + A + C. Т. к. по определению сумма R1 + R2 – постоянная величина, то, приравнивая, получаем:

A2 = B2 + C2

R1 + R2 = 2A.

45. Соотношение осей и расстояний гиперболы.

Теорема. Если R – расстояние от произвольной точки М гиперболы до какого - либо фокуса, D – расстояние от той же точки до соответствующей этому фокусу директрисы, то отношение R/D – величина постоянная, равная эксцентриситету.

Доказательство. Изобразим схематично гиперболу.

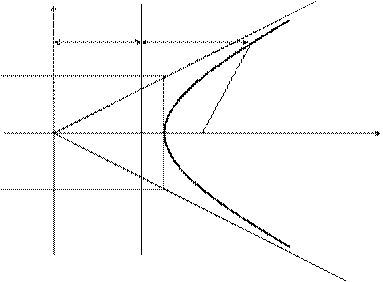y

a/e d

M(x, y)

r1

0 a F1 x

OF1 = c

Из очевидных геометрических соотношений можно записать:

A/e + d = x, следовательно d = x – a/e.

(x – c)2 + y2 = r2

Из канонического уравнения: 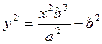, с учетом b2 = c2 – a2:

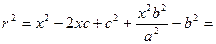
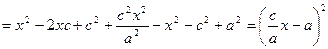
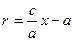
Тогда т. к. с/a = e, то r = ex – a.

Итого: .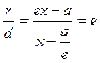

Для левой ветви гиперболы доказательство аналогично. Теорема доказана.

46. Эксцентриситет эллипса.

Форма эллипса определяется характеристикой, которая является отношением фокусного расстояния к большей оси и называется Эксцентриситетом.

Е = с/a.

Т. к. с < a, то е < 1.

Директрисы эллипса.

Директрисами эллипса называются две прямые, которые в канонической для эллипса системе координат имеют уравнения

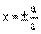или 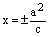. (13)

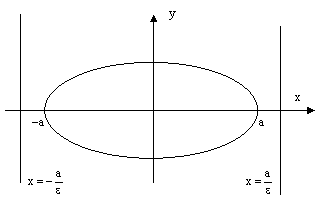
рис.8.

Теорема. Пусть М – произвольная точка эллипса, 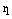, 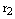– ее фокальные радиусы, 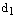– расстояние от точки М до левой директрисы, 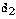– до правой. Тогда

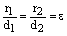, (14)

где 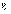– эксцентриситет эллипса.

Доказательство.

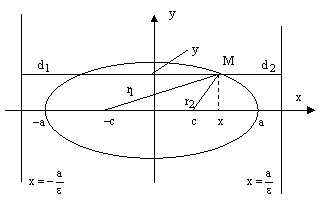
рис.9.

Пусть М(х, у) – координаты произвольной точки эллипса. Тогда

, ,

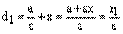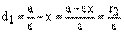откуда и следуют равенства (14).

Теорема доказана.

Эксцентриситет гиперболы,

По определению эксцентриситет гиперболы равен

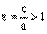. Зафиксируем действительную ось 2а и начнем изменять фокучное расстояние 2с. Так как 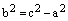, то при этом изменяется и величина b.

1) Пусть 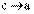. При этом 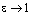, 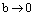и мнимые вершины 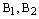стремятся к началу координат, асимптоты приближаются к оси Ох. Основной прямоугольник гиперболы вырождается в пределе в отрезок 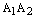, а сама гипербола вырождается в два луча на оси абсцисс: 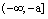и .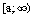

2) Пусть 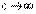. При этом 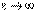, 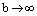и мнимые вершины 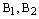стремятся к бесконечности, асимптоты приближаются к оси Оу. Основной прямоугольник гиперболы вытягивается вдоль оси ординат и ветви гиперболы приближаеются к прямым 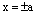и в пределе сливаются с ними. Гипербола вырождается в две прямые 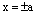, параллельные оси Оу.

Директрисы гиперболы.

Определение. Директрисами гиперболы называются две прямые,уравнения которых в канонической для гиперболы системе координат имеют вид .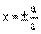

Так как 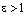, то .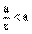

Обозначение. Расстояние между директрисами обозначается 2d и равно

.

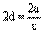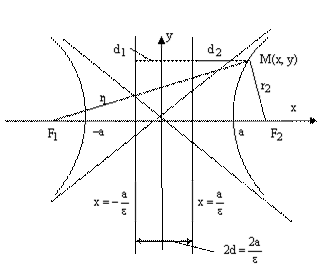
рис.8.

Теорема. Для любой точки гиперболы отношение ее фокального радиуса к расстоянию до соответствующей директрисы есть величина постоянная равная эксцентриситету:

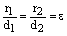. (7)

Доказательство. При выводе канонического уравнения гиперболы мы получили формулы для вычисления фокальных радиусов точки гиперболы с координатами М(х, у):

, ,

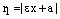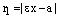где числа х, 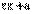и 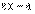имеют одинаковые знаки.

Из рисунка 8 мы видим, что при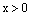

, ,

, ,

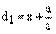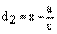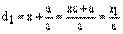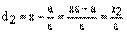откуда и следуют равенства (7). Аналогично доказываются формулы (7) и при .

Теорема доказана.

Парабола. Ее уравнение

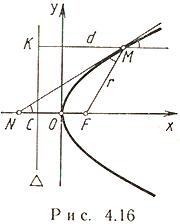
Пусть на плоскости заданы точка F и прямая 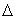, не проходящая через F. Парабола - множество всех тех точек M плоскости, каждая из которых равноудалена от точки F и прямой 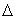. Точка F называется фокусом, прямая 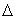- директрисой параболы; (OF) - ось, O - вершина, 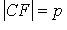- параметр, 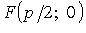- фокус, 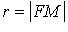- фокальный радиус.

Каноническое уравнение: