Пространственная система сил
Для равновесия пространственной произвольной системы сил, приложенной к твердому телу, необходимо и достаточно, чтобы суммы проекций на пространственные декартовы оси координат и суммы моментов всех сил системы относительно этих осей равнялись нулю:
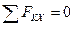 ,
, 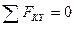 ,
, 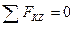 ,
,
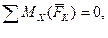
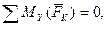
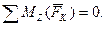
Если сила и данная ось не находятся в одной плоскости, то проецировать силу на эту ось следует согласно схеме, изображенной на рис. 12, а именно:
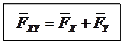
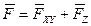 ,
, 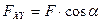 , ,
, ,
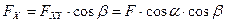 ,
,
|
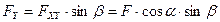 ,
, 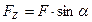 .
. 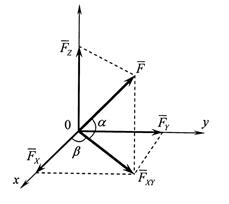
Рисунок 12 – Проекции силы на оси
Моментом силы относительно данной оси называется алгебраический момент проекции силы на плоскость перпендикулярную оси относительно точки пересечения оси и этой плоскости (рис. 13), т.е.:
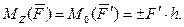
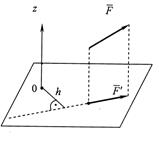
Рисунок 13 – Момент силы относительно оси
Момент считается положительным, если при наблюдении с положительного направления оси проекция силы 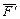 стремится вращать тело вокруг оси против часовой стрелки. В противном случае момент силы относительно данной оси считается отрицательным.
стремится вращать тело вокруг оси против часовой стрелки. В противном случае момент силы относительно данной оси считается отрицательным.
Для упрощения записи момента силы 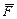 относительно оси бывает удобно разложить ее на составляющие
относительно оси бывает удобно разложить ее на составляющие 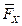 ,
, 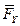 ,
, 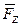 по координатным осям, тогда в соответствии с теоремой Вариньона моменты силы относительно этих осей будут равны:
по координатным осям, тогда в соответствии с теоремой Вариньона моменты силы относительно этих осей будут равны:
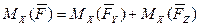 ,
,
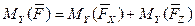 ,
,
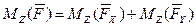 .
.
Моменты силы относительно координатных осей можно также записывать по аналитическим формулам:
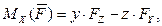
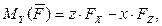
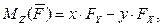
где x, y, z – координаты точки приложения силы;
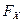 ,
, 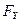 ,
, 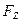 – проекции силы на оси координат.
– проекции силы на оси координат.
Пример 1. Однородная прямоугольная рама ABCD находится в равновесии. Вес рамы G=1 кН; Р=2 кН, 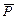 ||
|| 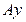 ; AD=BC=60 см; AB=CD=100 см;
; AD=BC=60 см; AB=CD=100 см; 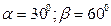 (рис. 14).
(рис. 14).
Найти реакции опор А и В (А – шаровой шарнир, В – петля (цилиндрический шарнир)), а также реакцию невесомого жесткого стержня СЕ.
Решение: Рассмотрим в равновесии раму ABCD. На раму действуют сила тяжести 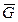 , сила
, сила 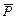 , реакция
, реакция 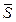 стержня СЕ и составляющие реакций опор А и В:
стержня СЕ и составляющие реакций опор А и В: 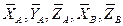 (рис. 15).
(рис. 15).
Составим шесть уравнений равновесия:
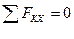 ;
; 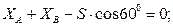 (1)
(1)
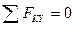 ;
; 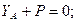 (2)
(2)
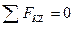 ;
; 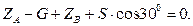 (3)
(3)
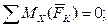
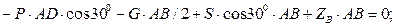 (4)
(4)
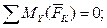
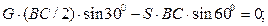 (5)
(5)
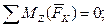
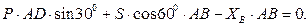 (6)
(6)
Из уравнении (1) – (6) находим:
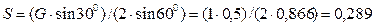 кН;
кН;
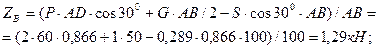
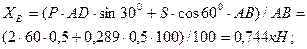
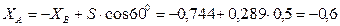 кН;
кН;
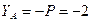 кН;
кН;
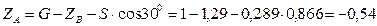 кН.
кН.
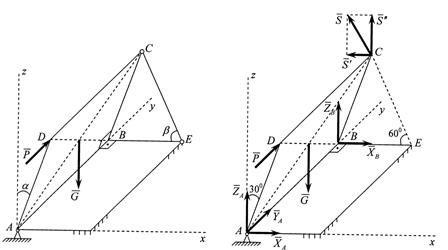
Рисунок 14 – К примеру 1 Рисунок 15 – К примеру 1
Пример 2. Твердое тело в виде двух однородных прямоугольных тонких плит, жестко соединенных между собой под прямым углом, находится в равновесии (рис. 16). Вес большей плиты Р1=5 кН, вес меньшей плиты Р2=3 кН. На тело действуют пара сил с моментом 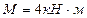 , лежащая в плоскости меньшей плиты, и силы F1=6 кН и F2=8 кН (
, лежащая в плоскости меньшей плиты, и силы F1=6 кН и F2=8 кН ( 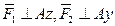 ).
).
Определить реакции опор А и В (А – шаровой шарнир, В – цилиндрический шарнир), а также реакцию невесомого жесткого стержня 1. При вычислениях принять а=0,6 м.
Решение: Рассмотрим в равновесии твердое тело, состоящее из двух однородных прямоугольных плит. На тело действуют силы тяжести 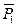 и
и 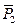 , силы
, силы 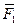 и
и 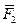 , пара сил с векторным моментом
, пара сил с векторным моментом 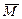
( 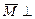 плоскости действия пары сил, т.е.
плоскости действия пары сил, т.е. 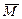 ||
|| 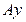 ), реакция стержня 1
), реакция стержня 1 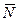 и составляющие реакций опор А и В:
и составляющие реакций опор А и В: 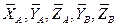 (рис. 17).
(рис. 17).
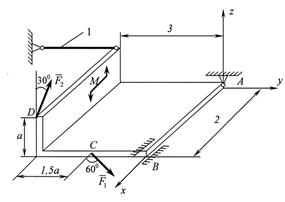
Рисунок 16– К примеру 2
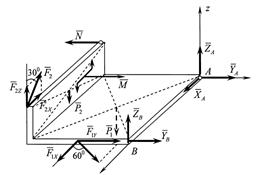
Рисунок 17 – К примеру 2
Для определения шести неизвестных реакций N, XA, YA, ZA, YB, ZB составляем шесть уравнений равновесия действующей на тело пространственной произвольной системы сил:
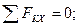
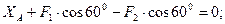 (7)
(7)
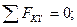
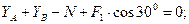 (8)
(8)
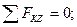
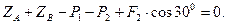 (9)
(9)
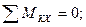
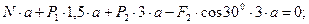 (10)
(10)
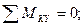
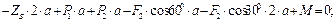 (11)
(11)
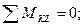
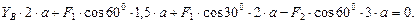 (12)
(12)
Для записи моментов сил 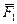 и
и 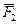 относительно осей координат раскладываем их на составляющие
относительно осей координат раскладываем их на составляющие 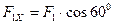 ,
, 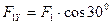 ,
, 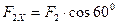 ,
, 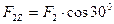 (эти составляющие входят в уравнения) и применяем теорему Вариньона.
(эти составляющие входят в уравнения) и применяем теорему Вариньона.
Далее решаем систему уравнений и находим неизвестные реакции:
Из уравнения (7) получаем:
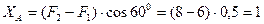 кН;
кН;
Из уравнения (10):
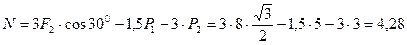 кН;
кН;
Из уравнения (11):
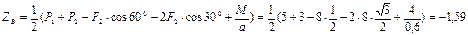
Из уравнения (9):
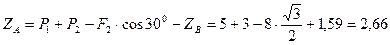 кН;
кН;
Из уравнения (12):
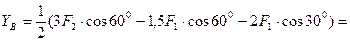
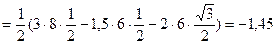 кН;
кН;
Из уравнения (8) :
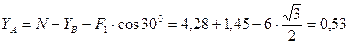 кН.
кН.
