Введение в стереометрию (10 ч)
МАТЕМАТИКА
Пояснительная записка
Математика занимает одно из центральных мест в образовании как важное средство формирования общей культуры, интеллектуального развития современного человека. Математические знания необходимы для изучения явлений природы, без них невозможно достижение успехов в развитии производства и науки. Знания о количественных отношениях и пространственных формах окружающего мира необходимы практически во всех сферах деятельности человека.
Методы, применяемые в математике, необходимы для специалистов в любой сфере деятельности, особенно в сфере наукоемких технических производств. Поэтому развитие компетенций у учащихся средствами учебного предмета для продолжения образования на уровнях профессионально-технического, среднего специального и высшего образования является особо важным.
Содержание математики как учебного предмета базируется на теоретической основе трех подходов: знаниевого, личностно ориентированного, компетентностного.
Цели и задачи изучения математики на базовом уровне при освоении содержания образовательной программы среднего образования:
• продолжение формирования представлений о математике как части общечеловеческой культуры, ее роли в познании явлений и процессов действительности;
• формирование математических знаний и умений, необходимых для изучения естественно-научных учебных предметов на базовом и повышенном уровнях и для продолжения образования в областях, не требующих углубленной математической подготовки;
• формирование репродуктивного, репродуктивно-продуктивного и творческого видов деятельности при решении учебных и прикладных задач;
• развитие логического мышления, пространственного воображения, алгоритмической культуры и критического мышления на уровне, необходимом в повседневной жизни и будущей профессиональной деятельности;
• воспитание культуры личности и личностных качеств (целеустремленность, самостоятельность, ответственность, самоконтроль и др.);
• формирование мотивации к самостоятельному приобретению математических знаний и умений, развитию компетенций, востребованных в условиях непрерывного образования и профессиональной деятельности.
Содержание алгебраического компонента в X классе предусматривает изучение тригонометрических и степенных функций, уравнений, неравенств, а содержание геометрического компонента — взаимное расположение прямых и плоскостей в пространстве, свойства прямых и плоскостей, метрические соотношения, основные геометрические тела.
Содержание алгебраического компонента в XI классе предусматривает изучение показательных и логарифмических функций, их свойств, показательных и логарифмических уравнений, неравенств, а содержание геометрического компонента — многогранники и их свойства, объемы и площади их поверхностей; тела вращения их свойства, объемы и площади их поверхностей.
Организация образовательного процесса
Образовательный процесс осуществляется с учетом возрастных особенностей учащихся, специфики учебного предмета, его места и роли в системе общего среднего образования.
Организация образовательного процесса должна быть направлена на достижение учащимися результатов, определенных настоящей учебной программой. Вместе с тем образовательный процесс должен быть поставлен так, чтобы у учащихся была возможность реализовать свои образовательные запросы. При этом необходимо, чтобы учащиеся не только усвоили определенные теоретические знания, но и научились использовать их при решении учебных задач и задач прикладного характера.
Обучение математике должно способствовать дальнейшему развитию культуры устной и письменной речи учащегося, умению работать с различными источниками информации, ставить цели, планировать и искать пути их достижения, анализировать и оценивать результаты.
Организуя образовательный процесс, учитель математики имеет право самостоятельно выбирать методы, приемы и технологии обучения, обеспечивающие достижение целей обучения и воспитания. Логическая строгость изложения учебного материала должна сочетаться с высокой степенью наглядности и доступности.
Образовательный процесс при изучении математики должен способствовать развитию интереса к овладению знаниями, способами познания окружающего мира; созданию положительного эмоционального состояния; формированию адекватной самооценки; эстетическому воспитанию учащихся.
X класс
СОДЕРЖАНИЕ УЧЕБНОГО ПРЕДМЕТА
140 ч (4 ч в неделю)
Алгебраический компонент — 84 ч
Геометрический компонент — 56 ч
Функция (15 ч)
Функция числового аргумента.Свойства функции (область определения, множество значений, нули функции, промежутки знакопостоянства функции, четность и нечетность, периодичность, возрастание и убывание, точки максимума и минимума, максимум и минимум, наибольшее и наименьшее значения функции на промежутке).
Построение графиков функций
y=f(x±a), y=f(x)±b, a,b ∈ R;
y=kf(x), k>0, k∈ R;
y=-f(x)
с помощью преобразования графика функции y=f(x).
Бесконечно убывающая геометрическая прогрессия как функция натурального аргумента. Сумма членов бесконечно убывающей геометрической прогрессии.
Основные требования
к результатам учебной деятельности учащихся
Учащиеся должны:
иметь представление о понятиях: функция числового аргумента, бесконечно убывающая геометрическая прогрессия как функция натурального аргумента;
знать термины и правильно применять понятия: область определения, множество значений, нули функции, промежутки знакопостоянства, четность и нечетность, периодичность и наименьший положительный период, возрастание и убывание, точки максимума и минимума, максимум и минимум функции, наибольшее и наименьшее значения функции на промежутке, бесконечно убывающая геометрическая прогрессия;
уметь:
• находить область определения и множество значений функции, нули функции, промежутки знакопостоянства, наименьший положительный период, промежутки возрастания и убывания, точки максимума и минимума, максимум и минимум функции, наибольшее и наименьшее значения функции на промежутке по аналитическому заданию функции и по графику функции;
• находить сумму членов бесконечно убывающей геометрической прогрессии;
• исследовать функцию на четность и нечетность по аналитическому заданию функции и по графику функции;
• выполнять построение графиков функций
y=f(x±a), y=f(x)±b, a,b ∈ R;
y=kf(x), k>0, k∈ R;
y=-f(x)
с помощью преобразования графика функции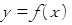 
.
Тригонометрия (40 ч)
Градусная и радианная мера произвольного угла. Единичная окружность. Определение синуса, косинуса, тангенса, котангенса произвольного угла.
Соотношения между синусом, косинусом, тангенсом и котангенсом одного и того же угла (тригонометрические тождества).
Тригонометрические функции числового аргумента. Их свойства и графики.
Арксинус, арккосинус, арктангенс и арккотангенс числа.
Простейшие тригонометрические уравнения sinx = a, cosx = a, tgx = a, сtgx = a и уравнения, сводящиеся к простейшим.
Формулы приведения, суммы и разности аргументов, двойного аргумента, преобразования суммы и разности тригонометрических функций в произведение.
Основные требования
к результатам учебной деятельности учащихся
Учащиеся должны:
знать термины и правильно применять понятия: единичная окружность, синус, косинус, тангенс, котангенс произвольного угла; тригонометрические функции числового аргумента; арксинус, арккосинус, арктангенс и арккотангенс числа;
знать:
• свойства тригонометрических функций числового аргумента;
• тригонометрические тождества; формулы приведения, суммы и разности аргументов, двойного аргумента, преобразования суммы и разности тригонометрических функций в произведение;
• числовые значения выражений sina, cosa при a, равном 0,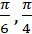 
, 
, 
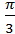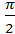,𝜋, 
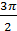,2𝜋 и tga, ctga для этих углов (в случае существования этих значений); значения выражений arcsina и arccosa при a, равном 0, ± 
, ± 
, ± 
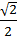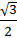, ±1, и выражений arctga и arcctga при a, равном 0, ± 
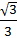, ±1,± 
;
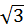• формулы решения простейших тригонометрических уравнений;
уметь:
• переводить градусную меру углов в радианную и наоборот;
• строить углы по их заданной градусной или радианной мере; использовать единичную окружность для нахождения значений синуса и косинуса заданных углов; строить углы по заданному значению их синуса, косинуса, тангенса;
• находить числовые значения тригонометрических выражений, используя значения тригонометрических функций и соответствующих формул;
• выполнять тождественные преобразования тригонометрических выражений с помощью тригонометрических формул;
• строить графики тригонометрических функций и применять свойства функций;
решать:простейшие тригонометрические уравнения и уравнения, сводящиеся к ним (методами разложения на множители, замены переменной), однородные тригонометрические уравнения.
Степень с рациональным показателем.
Степенная функция (25 ч)
Корень n-й степени из числа а (n≥2, n∈ N). Арифметический корень. Основные свойства корня n-й степени. Преобразование выражений, содержащих корни n-й степени.
Степень с рациональным показателем. Свойства степени с рациональным показателем. Степень с действительным показателем.
Степенная функция с рациональным показателем, свойства и график степенной функции.
Иррациональные уравнения.
Основные требования
к результатам учебной деятельности учащихся
Учащиеся должны:
иметь представление о степени с действительным показателем;
знать термины и правильно применять понятия: корень n-й степени из числа а, показатель степени корня, подкоренное выражение, степень с рациональным показателем, степенная функция, иррациональное уравнение;
знать:
• основные свойства корня n-й степени, свойства степеней с рациональным показателем; свойства и график степенной функции; формулы, выражающие свойства степеней и корней n-й степени;
• основные методы решения иррациональных уравнений;
уметь:
• вычислять корень n-й степени из действительного числа, представляющего n-ю степень; выносить множитель из-под корня; оценивать значение корня; представлять корень n-й степени в виде степени с рациональным показателем и наоборот; упрощать выражения, содержащие корни и степени с рациональным показателем;
• строить графики степенных функций y =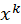 
для k ∈ Z, k≠0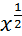, y= 
, y=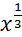 
;
• решать уравнения вида xn = a, где n ∈ N, a ∈ R; иррациональные уравнения.
XI класс
Содержание учебного предмета
140 ч (4 ч в неделю)
Алгебраический компонент — 84 ч
Геометрический компонент — 56 ч
Многогранники (10 ч)
Свойства призмы, правильной призмы, параллелепипеда. Площадь боковой и полной поверхностей призмы.
Свойства правильной пирамиды. Площадь боковой и полной поверхностей пирамиды. Усеченная пирамида.
Правильные многогранники.
Основные требования к результатам учебной деятельности учащихся
Учащиеся должны:
знать определения:призмы, прямой призмы, правильной призмы, параллелепипеда, куба, пирамиды, правильной пирамиды, усеченной пирамиды, диагонального сечения призмы и пирамиды;
знать свойства: призмы, прямой призмы, правильной призмы, параллелепипеда, прямоугольного параллелепипеда, куба, правильной пирамиды;
знать формулы:площади боковой поверхности прямой призмы, площади боковой поверхности правильной пирамиды;
иметь представление о правильных многогранниках;
уметь:
• применять формулы площади поверхности прямой призмы и правильной пирамиды к решению задач;
• выводить формулы площади боковой поверхности прямой призмы, площади боковой поверхности правильной пирамиды;
• решать геометрические задачи на доказательство и вычисление с использованием известных свойств призмы и пирамиды;
• применять полученные знания при решении задач практической направленности.
Объем многогранников (20 ч)
Объем тела. Объем прямоугольного параллелепипеда. Объем призмы. Объем пирамиды.
Основные требования к результатам учебной деятельности учащихся
Учащиеся должны:
знать формулы: объема параллелепипеда, призмы, пирамиды;
уметь:
• применять формулы объемов параллелепипеда, призмы и пирамиды к решению задач;
• решать геометрические задачи на доказательство и вычисление;
• применять полученные знания при решении задач практической направленности.
Тела вращения (17 ч)
Сфера и шар. Сечения сферы и шара плоскостью. Касательная плоскость к сфере (шару). Площадь сферы. Объем шара.
Цилиндр. Осевое сечение цилиндра. Развертка боковой поверхности цилиндра. Площадь боковой и полной поверхностей цилиндра. Объем цилиндра.
Конус. Осевое сечение конуса. Развертка боковой поверхности конуса. Площадь боковой и полной поверхностей конуса. Объем конуса.
Усеченный конус.
Основные требования к результатам учебной деятельности учащихся
Учащиеся должны:
знать определения: сферы, шара, радиуса, хорды, диаметра сферы (шара), касательной плоскости к сфере (шару), цилиндра, осевого сечения цилиндра, конуса, осевого сечения конуса, усеченного конуса;
знать формулы:площади сферы, объема шара, площади боковой и полной поверхности цилиндра, объема цилиндра, площади боковой и полной поверхности конуса, объема конуса;
иметь представление о сечении сферы и шара плоскостью, осевом сечении цилиндра, сечении, параллельном и перпендикулярном оси цилиндра, осевом сечении конуса и сечении, перпендикулярном оси конуса, развертке боковой поверхности цилиндра и конуса;
уметь:
• выводить формулы площади боковой поверхности цилиндра и конуса;
• находить объемы и площади поверхности тел вращения, решать задачи на доказательство и вычисление;
• применять полученные знания при решении задач практической направленности.
Резерв: 36 ч (27а + 7г)
МАТЕМАТИКА
Пояснительная записка
Математика занимает одно из центральных мест в образовании как важное средство формирования общей культуры, интеллектуального развития современного человека. Математические знания необходимы для изучения явлений природы, без них невозможно достижение успехов в развитии производства и науки. Знания о количественных отношениях и пространственных формах окружающего мира необходимы практически во всех сферах деятельности человека.
Методы, применяемые в математике, необходимы для специалистов в любой сфере деятельности, особенно в сфере наукоемких технических производств. Поэтому развитие компетенций у учащихся средствами учебного предмета для продолжения образования на уровнях профессионально-технического, среднего специального и высшего образования является особо важным.
Содержание математики как учебного предмета базируется на теоретической основе трех подходов: знаниевого, личностно ориентированного, компетентностного.
Цели и задачи изучения математики на базовом уровне при освоении содержания образовательной программы среднего образования:
• продолжение формирования представлений о математике как части общечеловеческой культуры, ее роли в познании явлений и процессов действительности;
• формирование математических знаний и умений, необходимых для изучения естественно-научных учебных предметов на базовом и повышенном уровнях и для продолжения образования в областях, не требующих углубленной математической подготовки;
• формирование репродуктивного, репродуктивно-продуктивного и творческого видов деятельности при решении учебных и прикладных задач;
• развитие логического мышления, пространственного воображения, алгоритмической культуры и критического мышления на уровне, необходимом в повседневной жизни и будущей профессиональной деятельности;
• воспитание культуры личности и личностных качеств (целеустремленность, самостоятельность, ответственность, самоконтроль и др.);
• формирование мотивации к самостоятельному приобретению математических знаний и умений, развитию компетенций, востребованных в условиях непрерывного образования и профессиональной деятельности.
Содержание алгебраического компонента в X классе предусматривает изучение тригонометрических и степенных функций, уравнений, неравенств, а содержание геометрического компонента — взаимное расположение прямых и плоскостей в пространстве, свойства прямых и плоскостей, метрические соотношения, основные геометрические тела.
Содержание алгебраического компонента в XI классе предусматривает изучение показательных и логарифмических функций, их свойств, показательных и логарифмических уравнений, неравенств, а содержание геометрического компонента — многогранники и их свойства, объемы и площади их поверхностей; тела вращения их свойства, объемы и площади их поверхностей.
Организация образовательного процесса
Образовательный процесс осуществляется с учетом возрастных особенностей учащихся, специфики учебного предмета, его места и роли в системе общего среднего образования.
Организация образовательного процесса должна быть направлена на достижение учащимися результатов, определенных настоящей учебной программой. Вместе с тем образовательный процесс должен быть поставлен так, чтобы у учащихся была возможность реализовать свои образовательные запросы. При этом необходимо, чтобы учащиеся не только усвоили определенные теоретические знания, но и научились использовать их при решении учебных задач и задач прикладного характера.
Обучение математике должно способствовать дальнейшему развитию культуры устной и письменной речи учащегося, умению работать с различными источниками информации, ставить цели, планировать и искать пути их достижения, анализировать и оценивать результаты.
Организуя образовательный процесс, учитель математики имеет право самостоятельно выбирать методы, приемы и технологии обучения, обеспечивающие достижение целей обучения и воспитания. Логическая строгость изложения учебного материала должна сочетаться с высокой степенью наглядности и доступности.
Образовательный процесс при изучении математики должен способствовать развитию интереса к овладению знаниями, способами познания окружающего мира; созданию положительного эмоционального состояния; формированию адекватной самооценки; эстетическому воспитанию учащихся.
X класс
СОДЕРЖАНИЕ УЧЕБНОГО ПРЕДМЕТА
140 ч (4 ч в неделю)
Алгебраический компонент — 84 ч
Геометрический компонент — 56 ч
Функция (15 ч)
Функция числового аргумента.Свойства функции (область определения, множество значений, нули функции, промежутки знакопостоянства функции, четность и нечетность, периодичность, возрастание и убывание, точки максимума и минимума, максимум и минимум, наибольшее и наименьшее значения функции на промежутке).
Построение графиков функций
y=f(x±a), y=f(x)±b, a,b ∈ R;
y=kf(x), k>0, k∈ R;
y=-f(x)
с помощью преобразования графика функции y=f(x).
Бесконечно убывающая геометрическая прогрессия как функция натурального аргумента. Сумма членов бесконечно убывающей геометрической прогрессии.
Основные требования
к результатам учебной деятельности учащихся
Учащиеся должны:
иметь представление о понятиях: функция числового аргумента, бесконечно убывающая геометрическая прогрессия как функция натурального аргумента;
знать термины и правильно применять понятия: область определения, множество значений, нули функции, промежутки знакопостоянства, четность и нечетность, периодичность и наименьший положительный период, возрастание и убывание, точки максимума и минимума, максимум и минимум функции, наибольшее и наименьшее значения функции на промежутке, бесконечно убывающая геометрическая прогрессия;
уметь:
• находить область определения и множество значений функции, нули функции, промежутки знакопостоянства, наименьший положительный период, промежутки возрастания и убывания, точки максимума и минимума, максимум и минимум функции, наибольшее и наименьшее значения функции на промежутке по аналитическому заданию функции и по графику функции;
• находить сумму членов бесконечно убывающей геометрической прогрессии;
• исследовать функцию на четность и нечетность по аналитическому заданию функции и по графику функции;
• выполнять построение графиков функций
y=f(x±a), y=f(x)±b, a,b ∈ R;
y=kf(x), k>0, k∈ R;
y=-f(x)
с помощью преобразования графика функции .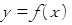
Тригонометрия (40 ч)
Градусная и радианная мера произвольного угла. Единичная окружность. Определение синуса, косинуса, тангенса, котангенса произвольного угла.
Соотношения между синусом, косинусом, тангенсом и котангенсом одного и того же угла (тригонометрические тождества).
Тригонометрические функции числового аргумента. Их свойства и графики.
Арксинус, арккосинус, арктангенс и арккотангенс числа.
Простейшие тригонометрические уравнения sinx = a, cosx = a, tgx = a, сtgx = a и уравнения, сводящиеся к простейшим.
Формулы приведения, суммы и разности аргументов, двойного аргумента, преобразования суммы и разности тригонометрических функций в произведение.
Основные требования
к результатам учебной деятельности учащихся
Учащиеся должны:
знать термины и правильно применять понятия: единичная окружность, синус, косинус, тангенс, котангенс произвольного угла; тригонометрические функции числового аргумента; арксинус, арккосинус, арктангенс и арккотангенс числа;
знать:
• свойства тригонометрических функций числового аргумента;
• тригонометрические тождества; формулы приведения, суммы и разности аргументов, двойного аргумента, преобразования суммы и разности тригонометрических функций в произведение;
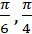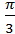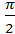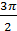• числовые значения выражений sina, cosa при a, равном 0, , , ,𝜋, ,2𝜋 и tga, ctga для этих углов (в случае существования этих значений); значения выражений arcsina и arccosa при a, равном 0, ± , ± , ± 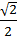, ±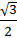1, и выражений arctga и arcctga при a, равном 0, ± 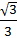, ±1,± ;
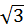• формулы решения простейших тригонометрических уравнений;
уметь:
• переводить градусную меру углов в радианную и наоборот;
• строить углы по их заданной градусной или радианной мере; использовать единичную окружность для нахождения значений синуса и косинуса заданных углов; строить углы по заданному значению их синуса, косинуса, тангенса;
• находить числовые значения тригонометрических выражений, используя значения тригонометрических функций и соответствующих формул;
• выполнять тождественные преобразования тригонометрических выражений с помощью тригонометрических формул;
• строить графики тригонометрических функций и применять свойства функций;
решать:простейшие тригонометрические уравнения и уравнения, сводящиеся к ним (методами разложения на множители, замены переменной), однородные тригонометрические уравнения.
Степень с рациональным показателем.
Степенная функция (25 ч)
Корень n-й степени из числа а (n≥2, n∈ N). Арифметический корень. Основные свойства корня n-й степени. Преобразование выражений, содержащих корни n-й степени.
Степень с рациональным показателем. Свойства степени с рациональным показателем. Степень с действительным показателем.
Степенная функция с рациональным показателем, свойства и график степенной функции.
Иррациональные уравнения.
Основные требования
к результатам учебной деятельности учащихся
Учащиеся должны:
иметь представление о степени с действительным показателем;
знать термины и правильно применять понятия: корень n-й степени из числа а, показатель степени корня, подкоренное выражение, степень с рациональным показателем, степенная функция, иррациональное уравнение;
знать:
• основные свойства корня n-й степени, свойства степеней с рациональным показателем; свойства и график степенной функции; формулы, выражающие свойства степеней и корней n-й степени;
• основные методы решения иррациональных уравнений;
уметь:
• вычислять корень n-й степени из действительного числа, представляющего n-ю степень; выносить множитель из-под корня; оценивать значение корня; представлять корень n-й степени в виде степени с рациональным показателем и наоборот; упрощать выражения, содержащие корни и степени с рациональным показателем;
• строить графики степенных функций y = 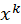для k ∈ Z, k≠0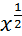, y= , y= ;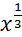
• решать уравнения вида xn = a, где n ∈ N, a ∈ R; иррациональные уравнения.
Введение в стереометрию (10 ч)
Предмет стереометрии. Пространственные тела. Многогранники: куб, параллелепипед, призма, прямая призма, правильная призма, пирамида, правильная пирамида.
Основные понятия стереометрии. Аксиомы стереометрии. Следствия из аксиом. Построение сечений многогранника плоскостью на основании аксиом стереометрии и следствий из них.
Основные требования
к результатам учебной деятельности учащихся
Учащиеся должны:
иметь представление о пространственных телах стереометрии: куб, параллелепипед, призма, прямая призма, правильная призма, пирамида, правильная пирамида;
знать: аксиомы и следствия из них;
уметь:
• применять аксиомы и следствия из них для решения задач;
• строить простейшие сечения многогранников плоскостью на основании аксиом и следствий их них.