Равномерная сходимость функционального ряда

О п р е д е л е н и е 9.Если последовательность 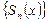частичных сумм ряда (5) сходится равномерно (сходится неравномерно) в области 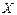к своей предельной функции 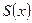, то говорят, что в области 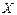ряд (5) сходится равномерно (сходится неравномерно).

Т е о р е м а 2 (критерий равномерной сходимости функционального ряда). Для того чтобы функциональный ряд (5) сходился равномерно в области 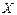, необходимо и достаточно выполнения условия:

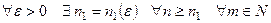
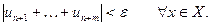
На практике для установления равномерной сходимости функционального ряда вида (5) полезно знание следующего достаточного признака.

Т е о р е м а 3 (признак Вейерштрасса). Если члены функционального ряда (5) удовлетворяют в области 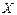неравенствам

,

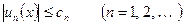где 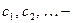члены некоторого сходящегося числового ряда 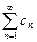, то ряд (5) сходится в области 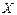равномерно.

ФУНКЦИОНАЛЬНЫЕ СВОЙСТВА СУММЫ РЯДА

С в о й с т в о 1 (непрерывность суммы). Если функции

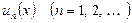
определены и непрерывны в области 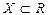и ряд (5) сходится в 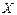равномерно к сумме 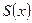, то функция 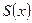непрерывна в области .

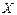З а м е ч а н и е 6. Сформулированные в свойстве 1 условия являются лишь достаточными: можно привести примеры равномерно сходящихся рядов с непрерывными членами и непрерывной суммой; а также можно привести примеры неравномерно сходящихся рядов с непрерывными членами и разрывной суммой.

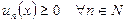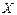З а м е ч а н и е 7. Если дополнительно к условиям, перечисленным в свойстве 1, функции на , то условие равномерной сходимости ряда (5) будет не только достаточным, но и необходимым для непрерывности суммы этого ряда.

С в о й с т в о 2 (почленный переход к пределу). Пусть любая из функций 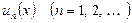определена в 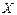и при 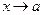имеет конечный предел: 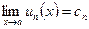. Если ряд (5) сходится в области 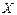равномерно, то сходится числовой ряд 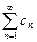и сумма 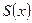ряда (5) при 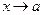имеет предел:

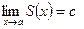, где 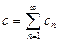, то есть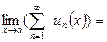

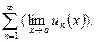
С в о й с т в о 3 (почленное интегрирование ряда). Если функции 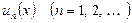непрерывны на отрезке 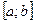и ряд (5) сходится равномерно на отрезке 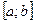, то интеграл от суммы 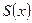ряда (5) существует и удовлетворяет равенству:

,

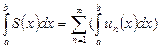то есть

.

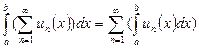С в о й с т в о 4 (почленное дифференцирование ряда). Пусть функции 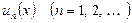имеют непрерывные производные 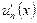в области 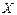. Если в 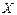не только сходится ряд (5), но равномерно сходится ряд 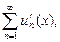то сумма 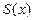ряда (5) имеет в 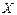производную. При этом справедливо равенство:

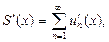то есть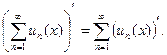

СТЕПЕННЫЕ РЯДЫ

О п р е д е л е н и е 10.Функциональный ряд

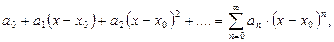(9)

где 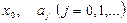– некоторые постоянные вещественные числа, называется степенным рядом с центром в точке 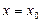. При этом числа 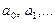называются коэффициентами степенного ряда (9).

З а м е ч а н и е 8.В дальнейшем мы ограничимся подробным анализом степенного ряда

(10)

с центром в точке 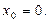Это не ограничит общности изложения, так как ряд (9) сводится к (10) с помощью замены: .

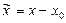Степенные ряды (9) и (10) определены при всех 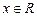, значит, для них областью определения ряда является .

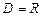З а м е ч а н и е 9. Любой степенной ряд (9) сходится абсолютно в точке 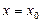. Следовательно, у любого степенного ряда область сходимости не является пустым множеством: центр ряда – точка 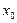– принадлежит .

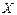Т е о р е м а 4(теорема Абеля). Если степенной ряд (10) сходится при 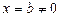, то он абсолютно сходится при всех 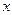, удовлетворяющих неравенству: 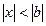. Если степенной ряд (10) расходится при 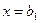, то он расходится при всех 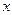, удовлетворяющих неравенству: .

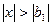З а м е ч а н и е 10.Из теоремы Абеля следует: у каждого степенного ряда (10) существует число 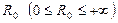, называемо радиусом сходимости ряда, что ряд (10) абсолютно сходится при 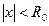, расходится при 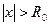. В этом случае промежуток 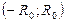называется интервалом сходимости ряда (10), внутри которого ряд (10) сходится абсолютно и вне которого – расходится.

В любой из точек 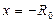и 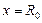(то есть на концах интервала сходимости ) ряд (10) может сходиться условно, сходиться абсолютно или расходиться, что зависит от рассматриваемого ряда. В соответствии с этим областью сходимости степенного ряда (10) будет одна из областей:

, .

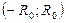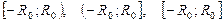З а м е ч а н и е 11.Радиус сходимости 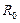степенного ряда (10) вычисляется по одной из формул:

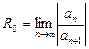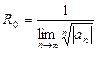или (11)

при условии существования этих пределов.

З а м е ч а н и е 12.Интервал сходимости 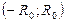ряда (10) можно найти без использования формул (11). Для этого достаточно найти (например, по признаку Даламбера) интервал сходимости абсолютного ряда .

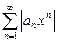З а м е ч а н и е 13.В случае ряда (9) его интервал сходимости имеет вид 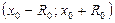, где число 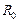вычисляется по одной из формул (11). Область сходимости ряда (9) совпадает с одним из промежутков: 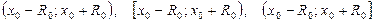или 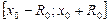в зависимости от условия примера.

СВОЙСТВА СТЕПЕННЫХ РЯДОВ

Пусть степенной ряд (10) имеет радиус сходимост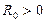и и 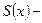его сумма при 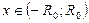. В этом случае говорят, что на интервале 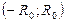функция 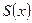разлагается в степенной ряд (10) и пишут:

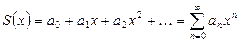. (12)

С в о й с т в о 1(о равномерной сходимости степенного ряда). Для любого числа 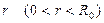степенной ряд (10) сходится равномерно по 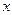в отрезке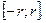

С в о й с т в о 2(о непрерывности суммы). Сумма 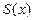степенного ряда (10) является непрерывной функцией в интервале 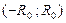сходимости ряда.

С в о й с т в о 3 (о тождестве степенных рядов). Если два степенных ряда 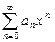и 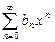в окрестности точки 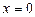имеют одну и ту же сумму, то эти ряды тождественны в том смысле, что .

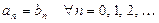С в о й с т в о 4 (о непрерывности на концах интервала сходимости). Если степенной ряд (10) сходится (хотя бы и не абсолютно) при 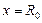( 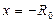) то его сумма 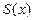непрерывна слева в точке 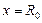(непрерывна справа в точке 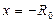), то есть

( ) .

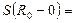
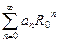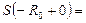
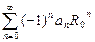С в о й с т в о 5(о почленном дифференцировании ряда). Сумма 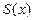степенного ряда (10) является дифференцируемой функцией в интервале сходимости ряда 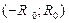. Ее производная 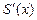есть сумма степенного ряда, полученного из (10) почленным дифференцированием по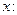

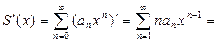
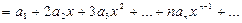. (13)

При этом интервал сходимости степенного ряда (13) равен .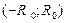

С в о й с т в о 6(о почленном интегрировании ряда). Сумма 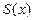степенного ряда (10) является интегрируемой функцией на любом отрезке 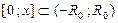. Интеграл 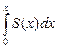есть сумма степенного ряда, полученного из (10) почленным интегрированием по 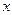от 0 до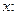

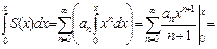
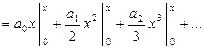
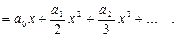(14)

При этом интервал сходимости степенного ряда (14) равен .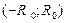

З а м е ч а н и е 14. Операции почленного дифференцирования и интегрирования степенных рядов можно проводить любое число раз. Получаемые при этом степенные ряды имеют одинаковый с исходным рядом интервал сходимости.

С в о й с т в о 7(арифметические операции со степенными рядами). Если степенные ряды 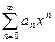и 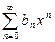имеют общий интервал сходимости 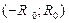, то в нем справедливы равенства:

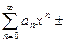
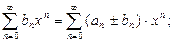
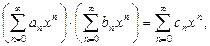где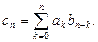

ПРИМЕРЫ С РЕШЕНИЯМИ

П р и м е р 1. Найти предельную функцию и определить характер сходимости функциональной последовательности

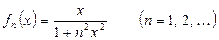(15)

на отрезке .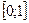

Р е ш е н и е. Для всех 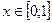справедливы неравенства:

.

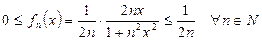Поэтому, выбрав произвольное число 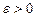, найдем номер 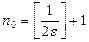, зависящий только от 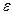, где обозначено: 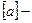целая часть числа 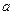. При таком выборе будет выполнено неравенство: 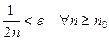. Значит,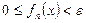 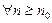для в с е х 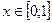. Следовательно, последовательность (15) имеет предельную функцию, причем

,

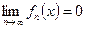
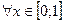Поэтому справедливо свойство:

.

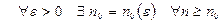
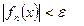
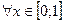О т в е т: сходится к функции 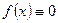равномерно на .

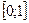П р и м е р 2.Найти предельную функцию и определить характер сходимости функциональной последовательности

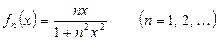(16)

на отрезке .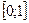

Р е ш е н и е. В данном случае для всех 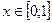справедливы неравенства:

,

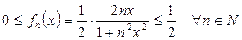причем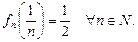

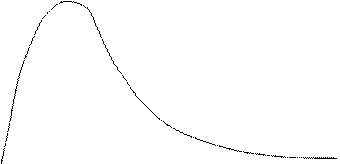
Это означает, что функция 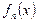достигает своего наибольшего значения, равного 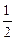, в точке 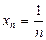(см. рис.1). Причем, если 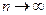, то

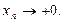
При любом ф и к с и р о в а н н о м 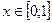справедливо неравенство:

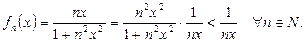
Значит, выбрав 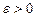, найдем номер 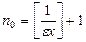, зависящи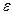й от и от 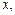что при всех 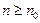имеем: 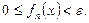Значит, для функций (16) справедливо равенство (2). Однако при этом не существует номера 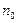, зависящего только от 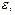который годился бы для всех 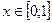, что наглядно следует из анализа функций на рис.1.

у

1/2

О 1/4 1/2 1 х Рис. 1

О т в е т: : сходится к функции 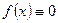неравномерно на .

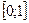П р и м е р 3. Найти область сходимости функционального ряда:

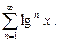(17)

Р ш е н и е. Функции 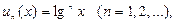являющиеся членами ряда (17), определены в области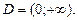

Заметим, что ряд (17) образован членами геометрической прогрессии 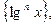первый член которой равен 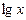и знаменатель 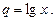Следовательно, ряд (17) сходится (абсолютно), если 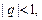и расходится, если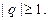

В рассматриваемом случае получаем:

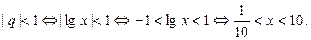
Поэтому область сходимости ряда (17) - интервал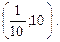

О т в е т: сходится абсолютно при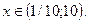

П р и м е р 4. Найти область сходимости функционального ряда:

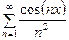. (18)

Р е ш е н и е. Рассмотрим вспомогательный ряд, являющийся абсолютным для ряда (18):

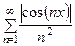. (19)

Заметим, что при любом фиксированном 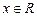справедливо неравенство: 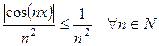. Причем ряд 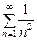, являющийся рядом Дирихле с показателем 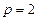, сходится. Значит, ряд (19) сходится в точке 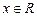по первому признаку сравнения положительных рядов. Но ряд (19) является абсолютным рядом для ряда (18) в точке .

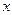Следовательно, при любом фиксированном 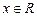ряд (18) сходится абсолютно и для него 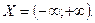Если проанализировать ряд (18) с помощью признака Вейерштрасса, получим: ряд сходится равномерно на .

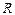О т в е т: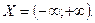

П р и м е р 5. Исследовать на сходимость ряд 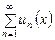, где

, .

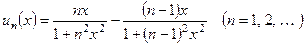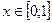Р е ш е н и е. Заметим, что для рассматриваемого ряда 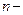я частичная сумма равна:

.

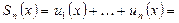
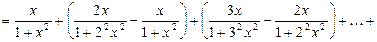
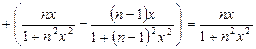Поэтому вопрос о сходимости функциональной последовательности 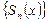равносилен вопросу о сходимости функциональной последовательности 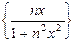, которая изучалась в примере 2.

Следовательно, воспользовавшись результатами примера 2 , заключаем: рассматриваемый ряд сходится на отрезке 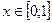к функции 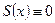(но сходится неравномерно).

О т в е т: сходится неравномерно.

П р и м е р 6. Найти область сходимости функционального ряда:

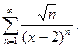(20)

Р е ш е н и е. В данном случае функции 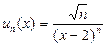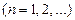, являющиеся членами ряда (20), определены при всех 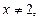то есть в области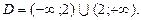

Исследуем ряд (20) на абсолютную сходимость. Для этого составим вспомогательный абсолютный ряд:

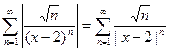. (21)

Члены ряда (21) задаются формулой: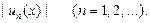

Вычислим предел:

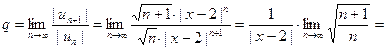
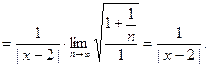
Следовательно, по признаку Даламбера ряд (21) сходится (а значит, ряд (20) сходится абсолютно), если 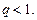Тогда

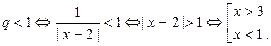
Итак, ряд (20) сходится абсолютно при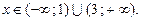

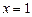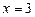При и признак Даламбера не дает ответа на вопрос о сходимости ряда (21). При 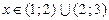абсолютный ряд (21) расходится. Но при 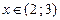исходный ряд (20) является положительным и совпадает со своим абсолютным рядом (21). Следовательно, при 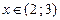ряд (20) расходится.

Таким образом, остается ответить на следующие вопросы:

а) сходится ли ряд (20) при 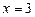; б) сходится ли ряд (20) при ;

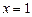в) сходится ли условно ряд (20) при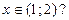

Изучим поставленные вопросы.

а) При 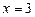ряд (20) является положительным числовым рядом. Он имеет вид 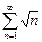и расходится по необходимому признаку сходимости числовых рядов: его общий член в пределе при 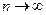не стремится к нулю.

б) При 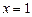ряд (20) имеет вид 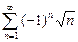и расходится по необходимому условию сходимости числовых рядов.

в) Возьмем произвольное число 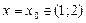и рассмотрим ряд (20) при 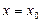. Он примет вид 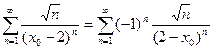и является знакочередующимся рядом.

Нетрудно видеть, что при 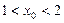имеем: 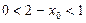и 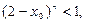причем 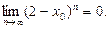Следовательно, 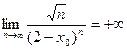, и изучаемый ряд расходится (по необходимому признаку сходимости числовых рядов).

Таким образом, ряд (20) абсолютно сходится при 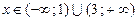и расходится при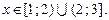

О т в е т: область сходимости ряда: 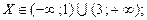во всех точках области 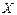ряд сходится абсолютно.

П р и м е р 7.Найти радиус и область сходимости степенного ряда: .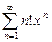

Р е ш е н и е. В данном случае .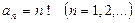

Для определения радиуса сходимости 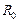воспользуемся первой формулой из (11):

.

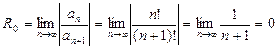Следовательно, 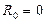, рассматриваемый ряд сходится абсолютно только при 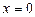. Значит, 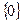– его область сходимости.

О т в е т. 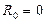; 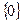– область сходимости.

П р и м е р 8.Найти радиус область сходимости степенного ряда: .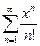

Р е ш е н и е. В данном случае 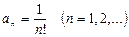. Поэтому, воспользовавшись первой из формул (11), находим радиус сходимости рассматриваемого ряда:

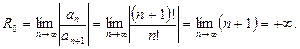
Следовательно, для данного в примере ряда 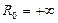. Значит, ряд абсолютно сходится при любом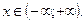

О т в е т: 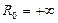; 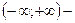область сходимости.

П р и м е р 9. Найти интервал сходимости степенного ряда:

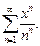(22)

Р е ш е н и е. Вычислим радиус сходимости ряда (22) по второй из формул (11), где для данного ряда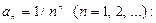

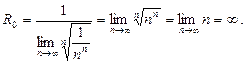
Следовательно, ряд (22) сходится (абсолютно) на интервале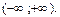

О т в е т: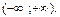

П р и м е р 10. Найти интервал и область сходимости степенного ряда:

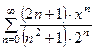. (23)

Р е ш е н и е. 1) Найдем интервал сходимости ряда (23). Для этого рассмотрим соответствующий абсолютный ряд:

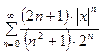. (24)

Применим к его исследованию признак Даламбера. Вычисляем:

.

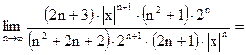
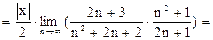
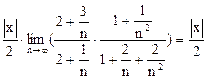Поэтому для сходимости ряда (24) потребуем выполнения условия:

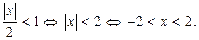
Значит, на интервале 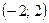ряд (23) сходится абсолютно. Вне этого интервала (при 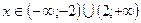) ряд (23) расходится. Таким образом, осталась неисследованной сходимость ряда (23) в точках 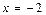и .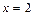

2) Исследуем поведение ряда (23) в точке .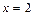

В этом случае ряд (23) превращается в положительный числовой ряд:

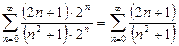. (25)

Сравним ряд (25) с гармоническим рядом 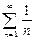. Так как

,

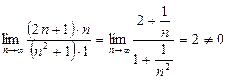то по второму признаку сравнения положительных рядов ряд (25) расходится в силу расходимости гармонического ряда.

Значит, точка 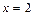не входит в область сходимости ряда (23).

3) Исследуем поведение ряда (23) в точке 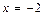. При 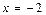ряд (23) превращается в знакочередующийся числовой ряд:

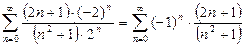. (26)

Заметим, что для ряда (26) абсолютным рядом является исследованный выше ряд (25). Так как мы установили расходимость ряда (25), то ряд (26) не сходится абсолютно.

Исследуем ряд (26) на условную сходимость. Для ряда (26) имеем: 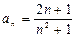. Проверим выполнение условий признака Лейбница.

а) .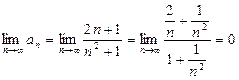

б) Исследуем функцию 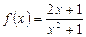на монотонность. Вычисляем: .

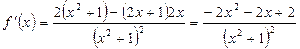Поэтому

.

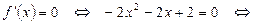
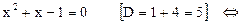
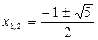Следовательно, имеем следующее расположение знаков функции :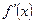

_ + _

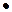
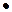х

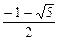
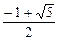
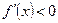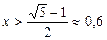Итак, при , то есть 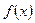убывает при всех .

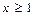Отсюда следует, что последовательность 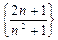является убывающей: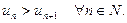

Следовательно, для ряда (26) выполнены все условия признака Лейбница, в силу чего ряд (26) сходится условно.

Значит, изучаемый степенной ряд (23) сходится условно при 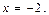Тем самым точка 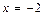входит в область сходимости ряда (23).

О т в е т: 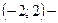интервал сходимости; 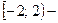область сходимости; ряд сходится абсолютно в интервале 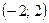; ряд сходится условно при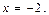

П р и м е р 11. Найти интервал сходимости и область сходимости степенного ряда:

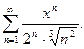(27)

Р е ш е н и е. 1) Найдем интервал сходимости ряда (27), где 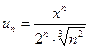. Вычислим предел:

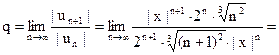
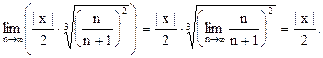
Следовательно, по признаку Даламбера ряд (27) абсолютно сходится при 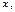удовлетворяющих неравенству: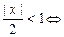 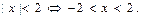Значит, 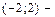интервал сходимости степенного ряда (27).

Для того чтобы найти область сходимости ряда (27), остается исследовать его на сходимость в точках 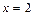и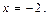

2) Исследуем ряд (27) на сходимость при 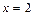. Заметим, что при 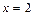ряд (27) имеет вид

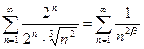
и является рядом Дирихле с показателем 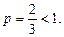Следовательно, при 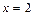ряд (27) расходится.

3) Исследуем ряд (27) на сходимость при 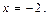При таком 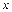ряд (27) имеет вид

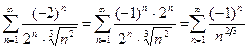(28)

и является знакочередующимся рядом. Причем, его абсолютный ряд 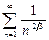расходится (как ряд Дирихле с показателем 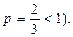Значит, при 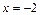ряд (27) не сходится абсолютно.

Проверим для ряда (28) условия теоремы Лейбница. Пусть 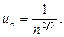Тогда имеем:

,

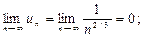
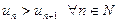так как

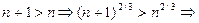
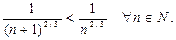
Следовательно, по признаку Лейбница при 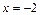ряд (27) сходится условно.

О т в е т: 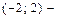интервал сходимости; 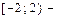область сходимости,

в точке 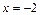ряд сходится условно, при 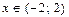ряд сходится абсолютно.

П р и м е р 12. Найти область сходимости степенного ряда:

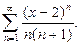(29)

Р е ш е н и е. 1) Найдем интервал сходимости ряда (29). Обозначим: 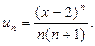Вычислим предел:

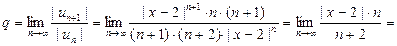
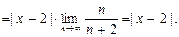
Следовательно, по признаку Даламбера исходный ряд (29) сходится абсолютно при 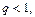то есть при 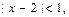что равносильно неравенству: 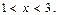Значит, 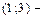интервал сходимости ряда (29).

2) Исследуем сходимость ряда (29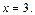) при При 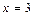ряд (29) имеет вид:

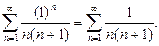
Это - положительный ряд. Сравним его со сходящимся рядом Дирихле 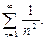Очевидно 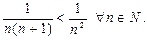Тогда по первому признаку сравнения ряд 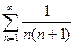сходится. Значит, ряд (29) сходится (абсолютно) при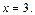

3) Исследуем сходимость ряда (29) при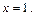

При 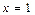ряд (29) имеет вид 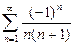и является знакочередующимся рядом. Его абсолютный ряд 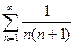сходится (как только что установлено выше). Следовательно, ряд (29) при 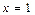сходится (абсолютно).

О т в е т: 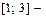область сходимости, для всех х ряд сходится абсолютно.

П р и м е р 13. Найти область сходимости ряда:

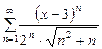. (30)

Р е ш е н и е. Ряд (30) является степенным рядом с центром в точке .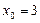

1) Найдем радиус сходимости ряда (30):

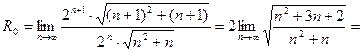
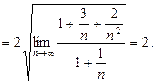
Следовательно, ряд (30) сходится абсолютно при

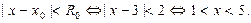
2) Исследуем ряд (30) на сходимость в точке 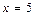, где он совпадает со следующим рядом:

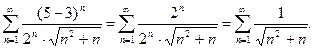
Полученный ряд является положительным. Он расходится по второму признаку сравнения, т.к. эквивалентен с точки зрения сходимости гармоническому ряду 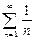, что следует из вычисленного ниже предела:

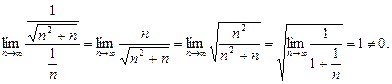
3) Исследуем ряд (30) на сходимость в точке 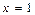, где он совпадает со следующим рядом:

.

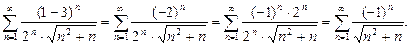Этот ряд является знакочередующимся. Его абсолютный ряд 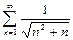расходится, доказано выше. Значит, ряд 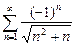не сходится абсолютно.

Исследуем ряд 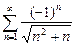на условную сходимость по признаку Лейбница. Обозначим: 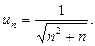Тогда получим: а)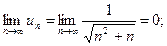

б) 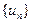убывает, так как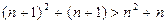 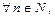откуда заключае