Абсолютно и условно сходящихся рядов

Т е о р е м а 3. Если ряд (4) сходится абсолютно, то он остается абсолютно сходящимся при любой перестановке его членов. При этом сумма ряда не зависит от порядка его членов.

Т е о р е м а 4. Если ряды и сходятся абсолютно, имея, соответственно, суммы и то сходится абсолютно ряд называемый произведением данных рядов, и его сумма равна

З а м е ч а н и е 8. В частности, если ряд (4) сходится абсолютно, имеет сумму то его квадратом называется ряд:

Он абсолютно сходится и имеет сумму

Т е о р е м а 5 (теорема Римана). Если ряд (1) сходится условно, то, выбрав произвольное число А, можно так переставить члены ряда (4), что сумма полученного таким образом ряда будет равна числу А. Более того, ряд, полученный из условно сходящегося ряда с помощью перестановки его членов, может оказаться расходящимся.

З а м е ч а н и е 8.Свойство, описанное в теореме Римана, связано с перестановкой бесконечного числа членов условно сходящегося ряда. Перестановка в таких рядах любого конечного числа членов не влияет ни на сходимость ряда, ни на его сумму.

ПРИМЕРЫ С РЕШЕНИЯМИ

П р и м е р 1. Исследовать сходимость ряда:

. (6)

Р е ш е н и е. Ряд (6) - знакочередующийся. Исследуем его на сходимость по признаку Лейбница. Проверим выполнение условий теоремы 1:

1) Так как для ряда (5) то

2) Так как и то, сравнивая числа и , получаем:

.

Следовательно, Поэтому последовательность является убывающей.

К аналогичному утверждению можно было прийти следующим образом: рассмотреть вспомогательную функцию на области и исследовать ее на монотонность.

В данном случае

.

Поэтому при заключаем: . Следовательно, функция убывает на Но Поэтому с ростом последовательность убывает. Итак, по признаку Лейбница ряд (6) сходится.

О т в е т: сходится.

П р и м е р 2. Исследовать сходимость ряда:

(7)

Р е ш е н и е. Очевидно, что ряд (7) является знакочередующимся рядом вида (1), где

Поэтому

откуда, используя свойства предела последовательности, заключаем:

Следовательно, для ряда (7) условие (2) признака Лейбница выполнено, а значит ряд (7) может быть сходящимся.

Убеждаемся, что последовательность не является монотонно убывающей. Действительно, заключаем:

но

Поэтому условие (3) не выполнено и признак Лейбница для ряда (7) не «работает».

Исследуем ряд (7) на сходимость по определению сходимости числовых рядов. Если ряд (7) сходится и его сумма равна числу , где где -я частичная сумма ряда (7). Причем в этом случае должно быть справедливо равенство:

Вычислим для ряда (7):

где -я частичная сумма гармонического ряда Но гармонический ряд расходится, то есть не существует конечного предела

Следовательно, не существует конечного предела Значит, ряд (7) расходится.

О т в е т: расходится.

П р и м е р 3. Исследовать сходимость ряда:

(8)

Р е ш е н и е. Ряд (8) имеет вид (1), где

Следовательно, получаем: . Поэтому и условие (2) для ряда (8) выполнено.

Однако условие монотонного убывания последовательности (8) нарушено, так как

и

Вычислим частичные суммы ряда (8):

Следовательно,

откуда следует существование предела и доказательство сходимости ряда (8).

О т в е т: сходится.

П р и м е р 4. Вычислить сумму ряда

(9)

приближенно с точностью до 0,01.

Р е ш е н и е. Проверим, что ряд (9) сходится. Действительно, ряд (9) является знакопеременным вида (1), где Причем

;

последовательность убывает, так как

Значит, по признаку Лейбница ряд (9) сходится.

Поэтому для приближенного вычисления суммы ряда (9) поступим в соответствии с замечанием 4: будем считать и число подберем в соответствии с требованием задачи: .

В рассматриваемом примере откуда для 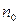получаем неравенство: Следовательно,

и

Поэтому в качестве числа 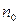можно взять любое целое число из неравенства , например .

Тогда получаем:

О т в е т:

П р и м е р 5. Исследовать ряд на сходимость:

(10)

Р е ш е н и е. Исследуем ряд на абсолютную сходимость. Составим вспомогательный абсолютный ряд:

Это - положительный ряд. Он сходится как ряд Дирихле с показателем . Следовательно, ряд (10) сходится по теореме 2, причем сходится абсолютно.

О т в е т: сходится абсолютно.

П р и м е р 6. Исследовать на абсолютную или условную сходимость ряд:

(11)

Р е ш е н и е. 1) Исследуем ряд (11) на абсолютную сходимость. Составим для (11) соответствующий ему абсолютный ряд:

(12)

Исследуем положительный ряд (12) на сходимость. Воспользуемся предельным признаком сравнения ряда (12) с расходящимся гармоническим рядом :

Следовательно, по второму признаку сравнения положительных рядов абсолютный ряд (12) расходится. Значит, исходный ряд (11) не сходится абсолютно. Но он при этом может сходиться условно или расходиться.

2) Исследуем ряд (11) на условную сходимость по признаку Лейбница (см. решение примера 1).

Итак, по признаку Лейбница ряд (11) сходится (условно).

О т в е т: сходится условно.

П р и м е р 7. Исследовать сходимость ряда:

Р е ш е н и е. Данный ряд - знакочередующийся. Для него общий член ряда задается формулой:

Причем . Поэтому .

Последовательность не является монотонно убывающей, так как

(т.е. но (т.е.

Следовательно, по признаку Лейбница данный в примере ряд расходится.

О т в е т: расходится.

П р и м е р 8. Исследовать ряд на абсолютную или условную сходимость:

(13)

Р е ш е н и е. Ряд (13) является знакопеременным в силу свойств функции

Исследуем ряд (13) на абсолютную сходимость. Для этого составим соответствующий ряду (13) абсолютный ряд:

(14)

Ряд (14) - положительный, причем Числовой ряд сходится, как ряд, составленный из членов убывающей геометрической прогрессии со знаменателем Следовательно, по первому признаку сравнения положительных рядов ряд (14) сходится.

Поэтому ряд (14) сходится абсолютно.

О т в е т: сходится абсолютно.

П р и м е р 9. Исследовать сходимость ряда:

где некоторое постоянное число. (15)

Р е ш е н и е. Составим для (15) вспомогательный абсолютный ряд:

(16)

Нетрудно видеть: так как то Ряд сходится как ряд, члены которого составляют убывающую геометрическую прогрессию.

Поэтому по первому признаку сравнения сходится положительный ряд (16). Следовательно, исходный ряд (15) сходится абсолютно.

О т в е т: сходится абсолютно.

П р и м е р 10. Исследовать сходимость ряда:

Р е ш е н и е. Данный в примере ряд - знакопеременный:

Составим абсолютный ряд: Здесь общий член Поэтому:

Следовательно, по радикальному признаку Коши абсолютный ряд сходится. Значит, исходный ряд сходится абсолютно.

О т в е т: сходится абсолютно.

П р и м е р 11. Найти квадрат ряда:

(17)

Р е ш е н и е. Предварительно убедимся, что ряд (19) сходится абсолютно. Для этого составим его абсолютный ряд и исследуем на сходимость, например, по признаку Даламбера. В данном случае

и

Следовательно, ряд (17) действительно сходится абсолютно.

Возведем ряд (17) в квадрат, воспользовавшись формулой:

(18)

Вычисляем:

Поэтому ряд (18) представим в виде:

.

О т в е т:

П р и м е р 12. Сравнить суммы рядов:

(19)

(20)

Р е ш е н и е. Заметим, что ряд (20) имеет вид

и получен из условно сходящегося ряда (19) перестановкой его членов по правилу: взят по порядку один положительный член, два отрицательных.

Для ряда (20) легко посчитать его сумму:

Следовательно, сумма ряда (20) в два раза меньше суммы ряда (19).

О т в е т:

ПРИМЕРЫ

Исследовать сходимость рядов по признаку Лейбница:

1. 2. 3. 4.

5. 6. 7.

8. 9. 10.

11. 12. 13.

Исследовать ряды на абсолютную и условную сходимость:

14. 15. 16. 17. 18.

19. 20. 21. 22.

23. 24. 25. 26.

27. 28. 29. 30.

31. 32. 33. 34. 35.

36. 37. 38. 39.

Исследовать сходимость рядов:

40. 41. 42. 43. 44.

45. 46. 47. 48. 49.

50. 51. 52. 53.

54. 55. 56. 57.

Проверить сходимость рядов и вычислить их суммы с точностью до 0,01:

58. 59.

ОТВЕТЫ

1.сходится.2.сходится. 3.расходится.4.сходится. 5.расходится.

6.сходится.7.расходится.8.сходится. 9.расходится. 10.сходится.

11.расходится. 12.сходится. 13.расходится. 14.сходится абсолютно.

15.сходится условно.16.сходится условно.17.сходится условно.18.сходится абсолютно. 19.сходится условно. 20.сходится абсолютно.

21.сходится условно. 22.сходится абсолютно. 23.сходится абсолютно.

24.сходится абсолютно. 25.сходится абсолютно. 26.сходится условно.

27.расходится. 28.сходится абсолютно. 29.сходится условно.

30.сходится абсолютно. 31.сходится абсолютно. 32.сходится условно.

33.сходится абсолютно. 34.сходится условно. 35.сходится абсолютно.

36.расходится. 37.сходится абсолютно. 38.сходится условно.

39.сходится абсолютно. 40.сходится. 41.расходится. 42.расходится.

43.сходится. 44.сходится. 45.сходится 46.сходится. 47.расходится.

48.сходится. 49.расходится. 50.расходится. 51.сходится. 52.расходится.

53.сходится. 54.расходится. 55.сходится. 56.сходится 57.расходится

58.0,96.59.0,04

§ 9. СТЕПЕННЫЕ РЯДЫ