Методы исследования нелинейных САР.
Для анализа нелинейную систему представляют в следующем виде (рис. 6.1).
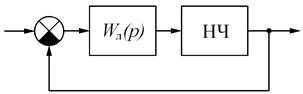
Рис. 6.1. Нелинейная САР
Поведение нелинейной системы, в отличие от линейной, включает еще один режим работы, который называется автоколебаниям, то есть выходная величина колеблется с постоянным периодом Tа и амплитудой A при отсутствии внешних колебательных воздействий (рис. 6.2).
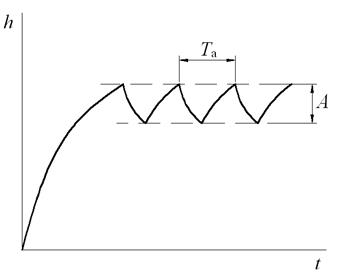
Рис. 6.2 – Автоколебания
Автоколебания могут быть устойчивыми и неустойчивыми. В последнем случае при изменении величины входного воздействия система срывается в неустойчивый режим работы.
Целью анализа нелинейной системы дополнительно является определение условий возникновения автоколебаний и их параметров.
Для анализа используют следующие методы.
1. Метод фазового пространства (точный).
Состояние системы, описываемой уравнением порядка n, может быть в любой момент времени определено значениями выходной величины и ее производных порядков до n – 1 включительно. Для каждого момента времени можно изобразить точку в пространстве, размерность которого равна n – 1 (для n = 2 такое пространство называется фазовой плоскостью, для систем более высокого порядка используют многомерное фазовое пространство). Совокупность точек при изменении времени называется фазовой траекторией, совокупность траекторий при различных начальных условиях – фазовым портретом. При анализе фазового портрета системы находят особые точки или траектории, по виду и расположению которых судят о поведении системы.
При анализе нелинейных систем фазовое пространство разбивают на участки для каждой части нелинейной характеристики. Если фазовый портрет содержит замкнутые траектории (предельные циклы), то в переходном процессе могут иметь место незатухающие колебания, то есть такой метод пригоден для анализа автоколебаний системы.
2. Метод моделирования (приближенный).
Нелинейные элементы заменяются приближенными линейными, которые анализируют с помощью вычислительных машин. Например, любая нелинейность может быть смоделирована с помощью набора операционных усилителей, резисторов, конденсаторов, индуктивностей и других электрических компонентов. Для анализа этих моделей используют аналоговые вычислительные машины (АВМ).
Цифровые методы моделирования основаны на использовании компьютерных программ (SIAM, VisSim, MATLAB).
3. Метод гармонической линеаризации (приближенный)
Нелинейное звено заменяют линейной моделью, которая сходным образом реагирует на входной сигнал:
Wн(jA) = g(A) + jb(A), где А – амплитуда гармонического сигнала.
Коэффициенты гармонической линеаризации (функции g(А) и b(А)) выбирают по справочникам в зависимости от вида нелинейности.
Большинство реализаций метода ориентировано на анализ автоколебаний в системе, например метод Гольдфарба. Систему представляют, как показано на рис. 6.3.
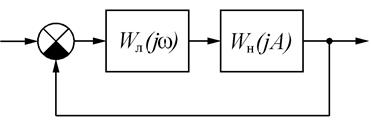
Рис. 6.3. Гармонически линеаризованная САР
Условия существования автоколебаний в системе:
1 + Wн(jA) + Wл(jω) = 0
Уравнение приводится к виду Wл(jω) = –1/Wн(jA) и решается графически, как показано на рис. 6.4.
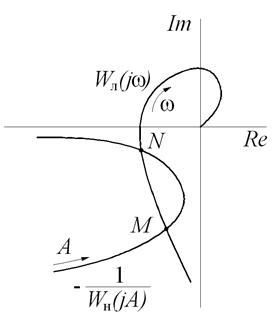
Рис. 6.4. Решение уравнения автоколебаний
Если графики имеют точку пересечения, то в системе возможны автоколебания, частота которых определяется по АФЧХ линейной части, амплитуда – по обратной характеристике нелинейной части.
В соответствии с рис. 6.4 в системе будут иметь место автоколебания с частотами ωN и ωM, причем колебания с частотой ωN будут устойчивыми с амплитудой AN (график –1/Wн(jA) входит в контур АФЧХ), а с частотой ωM – неустойчивыми (график –1/Wн(jA) выходит из контура АФЧХ).
4. Метод Попова для оценки устойчивости (точный).
Метод позволяет получить качественную оценку устойчивости. Его применяют для систем с одной однозначной нелинейностью. Для оценки устойчивости записывают передаточную функцию линейной части. Характеристическое уравнение линейной части должно иметь не более двух нулевых корней, остальные корни должны иметь отрицательные вещественные части. Эту передаточную функцию видоизменяют следующим образом:
ReW*(jω) = ReW(jω); ImW*(jω) = ωImW(jω)
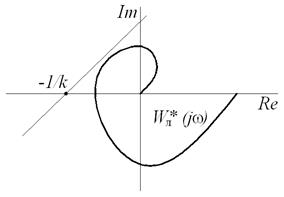
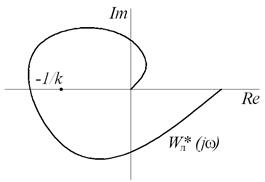
Система будет устойчивой, если на комплексной плоскости можно провести прямую через точку с координатами (–1/k; j0) таким образом, чтобы годограф видоизмененной частотной передаточной функции полностью находился правее и ниже этой прямой (рис. 6.5). Критерий Попова является достаточным условием устойчивости, при этом необходимым условием является расположение обычного (не видоизмененного) годографа линейной части – он не должен пересекать действительную ось левее точки (–1/k; j0). Величина k определяется по графику нелинейности с помощью прямой, под которой располагается график (на рис. 6.6)
 а) а) | 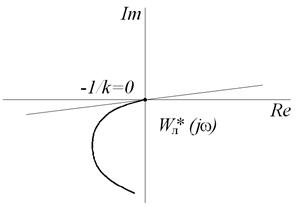 б) б) |
 в) в) |
Рис. 6.5. Критерий Попова: а, б – система устойчива, в – система неустойчива
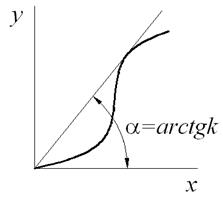
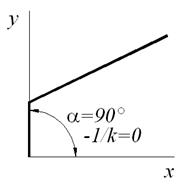
Рис. 6.6. Определение коэффициента k
Примером нелинейной системы может служить двухпозиционная САР температуры (рис. 6.7). В таких системах один из элементов (в данном случае это ртутный контактный термометр) имеет нелинейность в виде двухпозиционной релейной характеристики.
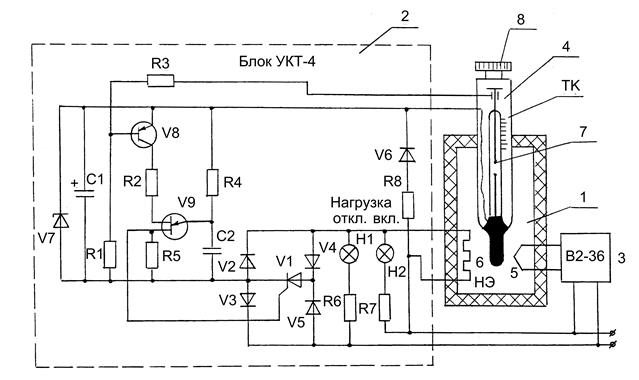
Рис. 6.7. САР температуры
1 – термокамера; 2 – блок УТК-4; 3 – вольтметр; 4 – контактный термометр; 5 – термопара; 6 – нагревательный элемент; 7 – регулируемый контакт; 8 – винт для перемещения регулируемого контакта.
Принцип работы терморегулятора заключается в том, что сигнал с контактного датчика температуры используется для поддержания необходимого температурного режима. По принципу действия усилительное устройство УТК-4 представляет собой тиристорный выключатель, управляемый генератором на однопереходном транзисторе (ОПТ) и транзисторным ключом. УТК-4 работает следующим образом. После подачи питающего напряжения на устройство при разомкнутых контактах термоконтактора ТК транзистор V8 открыт отрицательным потенциалом, подаваемым на его базу через резистор R1. Генератор на ОПТ, состоящий из однопереходного транзистора V9, резисторов R2, R4, R5 и конденсатора C2, включается работу и генерирует ряд импульсов с частотой около 7,5 кГц. Эти импульсы открывают тиристор V1, осуществляя тем самым подключение нагрузки НЭ к цепи переменного тока. Контакты ТК при этом находятся под напряжением, не превышая величины падения напряжения на переходе открытого транзистора V8 (не более 0,5 В).
При замыкании контактов ТК транзистор V8 закрывается, базовая цепь однопереходного транзистора обесточивается, генератор на ОПТ прекращает свою работу, и тиристор отключает нагрузку от цепи переменного тока. Ток, проходящий через замкнутые контакты ТК, при этом определяется напряжением питания схемы управления и величиной суммы сопротивлений R1 + R3 (около 0,2 А).
Питание схемы управления осуществляется от сети переменного тока через гасящий резистор R8, выпрямитель V6, стабилитрон V7 и сглаживающий конденсатор С1.
Литература: [1, c. 242 – 264] , [2, c. 194 – 336], [3. с.599 – 784]
ИМПУЛЬСНЫЕ И ЦИФРОВЫЕ САР
Модели импульсных САР
Импульсной называется система, в состав которой входит хотя бы одно звено, которое преобразует непрерывный сигнал в последовательность импульсов равноотстоящих по времени. Основной элемент импульсной системы – это импульсный фильтр, который представляет собой комбинацию импульсного элемента и непрерывной части (рис. 7.1).
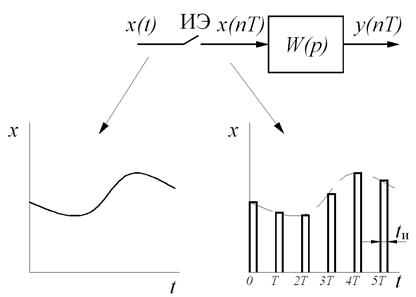
Рис. 7.1. Импульсный фильтр
Если длительность импульса намного меньше периода следования (tи<<T), то сигнал на выходе импульсного фильтра можно представить как сумму функций веса непрерывной части, определенных в моменты времен 0, T, 2T, …:
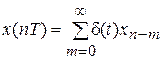
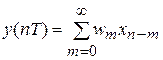
Для математического описания импульсных фильтров используют дискретное преобразование Лапласа и соответствующую дискретную передаточную функцию W(z); z = epT = ejωT.
Передаточную функцию импульсного фильтра получают следующим образом:
1) для непрерывной части находят функцию веса как переход от изображения Лапласа (передаточной функции) к оригиналу;
2) для функции веса по таблицам находят z-преобразование.
Например:
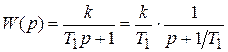
По таблицам преобразования Лапласа 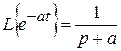 , следовательно
, следовательно
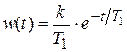 .
.
По таблицам для z-преобразования
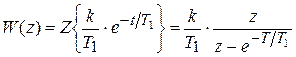 .
.
Если длительностью импульсов невозможно пренебречь, W(z) определяют с использованием модифицированного дискретного преобразования Лапласа:
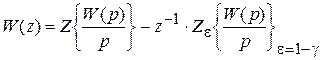 ,
, 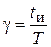 .
.
Например:
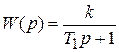
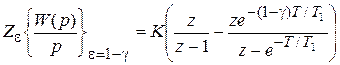
При e = 0
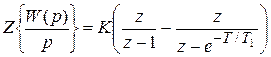
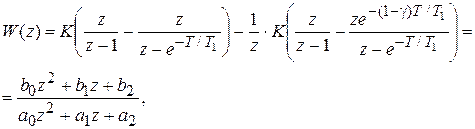
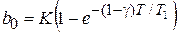 ,
, 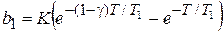 ,
,
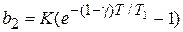 , a0 = 1,
, a0 = 1, 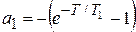 ,
, 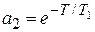 .
.
В отличие от импульсной системы, цифровая система имеет более сложную структуру (рис. 7.2).
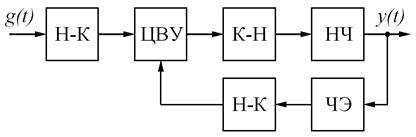
Рис. 7.2. Цифровая САР
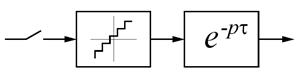
ЦВУ (цифровое вычислительное устройство) выполняет функции сравнивающего устройства, а также некоторые функции по преобразованию сигнала. Кроме того, в составе системы имеется преобразователь непрерывного сигнала в код (Н–К, АЦП) и преобразователь кодового сигнала в непрерывный (К–Н, ЦАП). В некоторых случаях ЦВУ может также выполнять функцию задающего устройства, то есть задающее воздействие формируется программой. Модели элементов цифровой САР показаны на рис. 7.3.

а)
б)

в)
Рис. 7.3. Элементы цифровой САР
а – ЦВУ, б – АЦП, в – ЦАП
Все модели являются импульсными и имеют нелинейность типа «квантователь», так как работают с цифровыми сигналами. Звено чистого запаздывания позволяет учесть затраты времени на выполнение программы ЦВУ, аналого-цифровое и цифро-аналоговое преобразование. Экстраполятор Э преобразует цифровой сигнал в непрерывный (рис. 7.4). Передаточная функция экстраполятора нулевого порядка
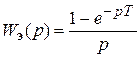 ,
,
первого порядка
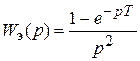 .
.
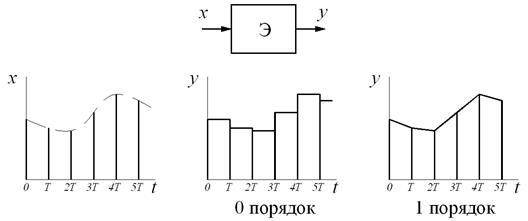
Рис. 7.4. Сигналы на входе и выходе экстраполятора
Как правило, используются коды с достаточно большим числом разрядов. Поэтому нелинейностью, возникающей при квантовании сигналов, можно пренебречь и рассматривать цифровые системы как линейные импульсные.
