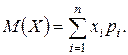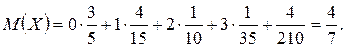Произвольные дискретные распределения

Пример 1. Дискретная СВ X задана рядом распределения.

X
P	0,3	0,2	0,1	0,3	0,1

Найти: 1) функцию распределения F(x);

2) M(X), D(X), s(X), моду M₀(X);

3) P(2≤ X < 8).

Решение. 1) Найдем функцию распределения F(x) и построим ее график. Для дискретной СВ X по формуле (1.8)

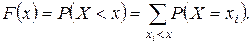
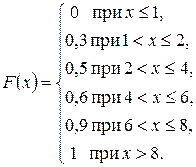
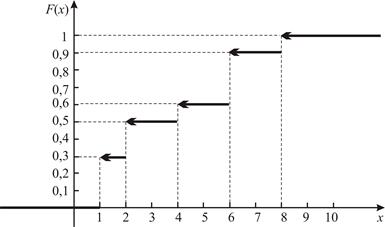
2) Найдем числовые характеристики распределения ДСВ X. По определению математическое ожидание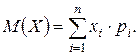

M(X) = 1 × 0,3 + 2 × 0,2 + 4 × 0,1 + 6 × 0,3 + 8 × 0,1 =

= 0,3 + 0,4 + 0,4 +1,8 + 0,8 = 3,7.

Для вычисления дисперсии D(X) используем формулу (1.21) 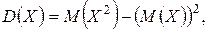где

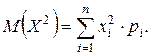
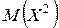= 1² × 0,3 + 2² × 0,2 + 4² × 0,1 + 6² × 0,3 + 8² × 0,1 =

= 0,3 + 0,8 + 1,6 +10,8 + 6,4 = 19,9

D(X) = 19,9 – (3,7)² = 6,21.

По формуле (1.22) найдем среднее квадратическое отклонение,

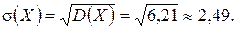
Данное распределение является бимодальным, так как максимальная вероятность p = 0,3 соответствует двум значениям СВ X.

M₀ = 1 или M₀ = 6

3) Найдем вероятность P(2≤ X < 8).

При непосредственном вычислении вероятность равна

P(2≤ X < 8) = P(X = 2) + P(X = 4) + P(X = 6) = 0,2 + 0,1 + 0,3 = 0,6

Если используем функцию распределения, то получим тот же результат.

P(2≤ X < 8) = F(8) – F(2) = 0,9 – 0,3 = 0,6.

Пример 2. В партии из 10 изделий 6 изделий высшего сорта и 4 первосортных. Наудачу выбираются 3 изделия. Составить ряд распределения случайной величины X – числа изделий первого сорта среди отобранных. Найти M(X) и s(X).

Решение. Дискретная случайная величина X может принимать следующие значения: x₁ = 0, x₂ = 1, x₃ = 2, x₄ = 3. Распределение СВ X – гипергеометрическое, с параметрами N = 10, M = 4, n = 3.

В соответствии с общей формулой (1.31)

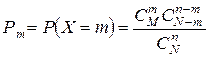
можно утверждать, что для рассматриваемого примера

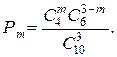
Используя эту формулу, получим:

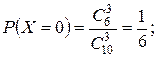
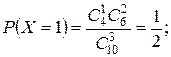
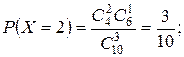
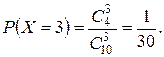
Выполним проверку:

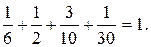
Составим ряд распределения случайной величины X:

xi
pi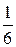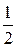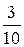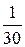

Найдем M(X) по формуле (1.16)

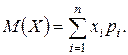
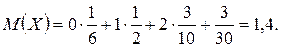
По формуле (1.22)

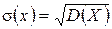
найдем среднее квадратическое отклонение, при этом для вычисления дисперсии D(X) воспользуемся формулой (1.21)

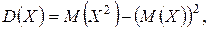где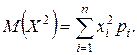

Тогда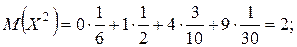

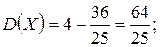
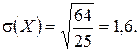
Пример 3. В партии из 10 изделий 6 изделий высшего сорта и 4 первосортных. Наудачу по одному, одно за другим, без возвращения в партию выбираются изделия до тех пор, пока не будет выбрано изделие высшего сорта. Составить ряд распределения случайной величины X – числа отобранных при этом изделий первого сорта. Найти F(X) и M(X).

Решение. Множество возможных значений дискретной случайной величины X: {0; 1; 2; 3; 4}.

Найдем вероятности, соответствующие этим значениям.

Пусть событие А_i – i-ое выбранное изделие первого сорта. Тогда 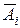– i-ое выбранное изделие высшего сорта. Так как события A_i зависимые, то при определении вероятностей P(X = x_i) будем использовать теорему умножения вероятностей для зависимых сомножителей.

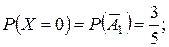
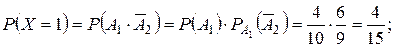
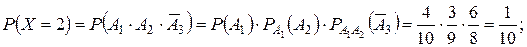
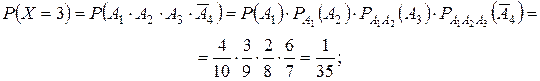
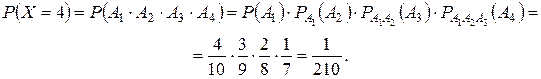
Выполним проверку:

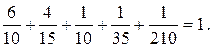
Составим ряд распределения СВ X:

xi
pi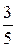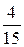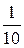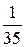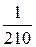

Найдем функцию распределения F(x). Для этого разделим числовую ось на непересекающиеся промежутки возможными значениями случайной величины X и найдем значения F(x) на каждом из промежутков, используя формулу (1.8)

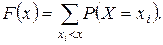
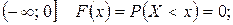
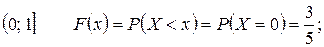
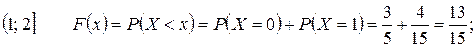
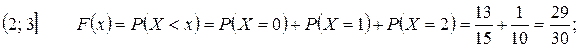
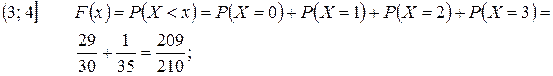
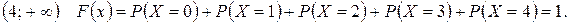
Итак,

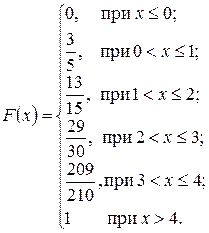
Найдем M(X) по формуле (1.16)