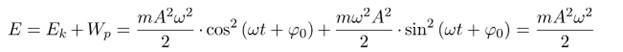Гармонические колебания и их характеристики. Гармонические осцилляторы. Энергия гармонических колебаний.

Билет №1

Гармонические колебания и их характеристики. Гармонические осцилляторы. Энергия гармонических колебаний.

Колебания – это движения, которые более менее периодически повторяются во времени. Система, совершающая колебания – колебательная система.

Гармонические колебания —колебания, происходящие по закону sin или cos.

Уравнение гармонического колебания имеет вид

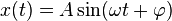
или

,

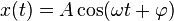где х смещение тела от положения равновесия;

А — амплитуда колебания, т.е. максимальное смещение тела от положения равновесия;

(радиан/с, градус/с) = , циклическая частота гармонических колебаний

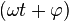(радиан, градус) — полная фаза колебания. Определяет значение x в любой момент времени

0 (радиан, градус) — начальная фаза колебаний

Начальная фаза – определяет значение x в значении t=0, x=

По 2ому закону Ньютона диф.уравнение гармонических колебаний:

Где 𝜔𝑜 = √ 𝑘/𝑚 – собственная частота или частота гармонических колебаний

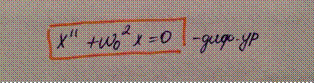
Гармонический осциллятор - это колебательная система, совершающая гармонические колебания.

• Пружинный маятник

F= -kx (Закон Гука)

X<< l малые или упругие деформации

Fсопр= 0

• Механический маятник 𝜔𝑜 = √ 𝑘/ 𝑚 , 𝑇𝑜 = 2𝜋√𝑚/𝑘 зависит от массы тел

• Математический маятник

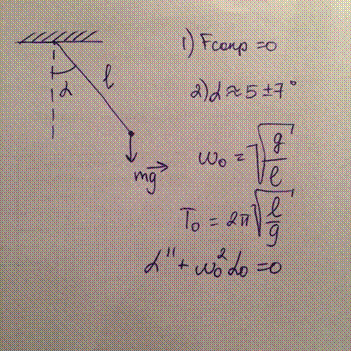
• Физический маятник – твердое тело, совершающее колебания вокруг оси, не проходящей через центр тяжести тела.

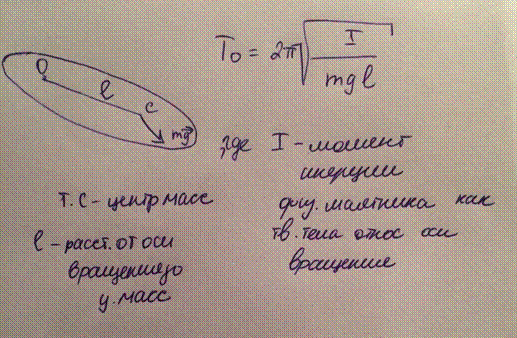
Полная энергия гармонических колебаний равна сумме кинетической энергии и потенциальной энергии

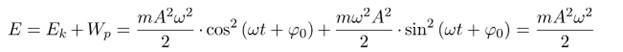
Соединения деталей. Разъемные и неразъемные соединения

Разъемные соединения - соединения, разборка которых происходит без нарушения целостности составных частей изделия.

4. Проверить прочность на изгиб вала диаметром d = 40 мм, если наибольший изгибающий момент на этом валу равен М_и = 400 Нм. Допустимое напряжение для материала вала .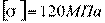

5. Найти скорость течения газа по трубе, если известно, что за время t=5мин через поперечное сечение трубы протекает масса газа m=50 кг. Плотность газа 7,5 кг/м³. Диаметр трубы 0,5 м.

БИЛЕТ 2

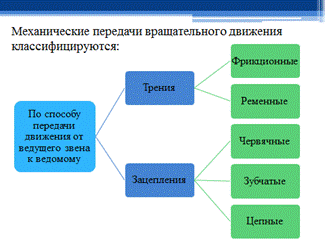
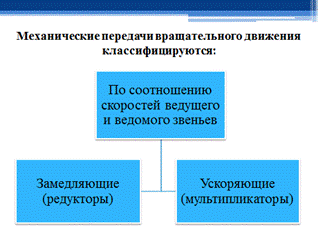
Классификация деталей и передаточных механизмов.

Механические передачи - устройства, служащие для передачи и преобразования механической энергии от энергетической машины к исполнительному механизму.

4. Насколько увеличится осадка теплохода у морской пристани в результате погрузки груза массой m=3т, если площадь сечения теплохода по ватерлинии S=5000м²? Плотность морской воды 1030 кг/м³.

5.Рассчитать диаметр вала по условию его прочности на кручение, если крутящий момент на валу М_к = 600 Нм, а допускаемое напряжение при кручении для материала вала .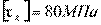

БИЛЕТ 3

БИЛЕТ 4

БИЛЕТ 5

1. Выталкивающая сила. Закон Архимеда. Подъемная сила.

Закон Архимеда.Выталкивающая сила есть сила Архимеда, определяющая закон Архимеда

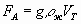
На тело, погруженное в жидкость или газ действует выталкивающая сила равна весу вытесненной жидкости в объеме погруженной части тела.

Fa=*g*Vвыт.ж где Vвыт.ж= V погруженной части тела

Условия плавания тел.

Поведение тела, находящегося в жидкости или газе, зависит от соотношения между модулями силы тяжести Fт и архимедовой силы FА, которые действуют на это тело. Возможны следующие три случая:

Fт > FА – тело тонет;

Fт = FА – тело плавает в жидкости или газе;

Fт < FА – тело всплывает до тех пор, пока не начнет плавать.

11. Что такое подъемная сила?

Подъемная сила – разница между силой архимеда и mg

Подъёмная сила — составляющая полной силы давления жидкой или газообразной среды на движущееся в ней тело; направлена перпендикулярно скорости движения тела.

БИЛЕТ 6

1. Уравнение неразрывности. Уравнение Бернулли.

Уравнение неразрывности

За единицу времени через каждое сечение протекает одинаковая масса или объем жидкости

m/t=ρV/t=ρSl/t=ρSѴ=const

Массовый расход = const

SѴ=const

S1Ѵ1=S2Ѵ2 –ур-е неразрывности жидкости (газа)

S1/S2=Ѵ2/Ѵ1

Уравнение Бернулли

Для 2х сечений:

p1+ρV^2/2 +pgh1=p2+ρV^2/2+pgh2

Для каждого сечения

p+ρV^2/2 +pgh=const

где p – статическое давление, ρV^2/2 – динамич давление, pgh – гидростатич давление

БИЛЕТ 7

БИЛЕТ 8

БИЛЕТ 9

БИЛЕТ 10

БИЛЕТ 11

Малый поршень гидравлического пресса за один ход опускается на расстояние 50 см, а большой поршень поднимается на 5 см. С какой силой действует пресс на зажатое в нем тело, если на малый поршень действует сила, равная 500 Н. КПД пресса 0,98.

(НЕ УВЕРЕНА)

Работа по перемещению малого поршня Ам = Fм * hм = F1 * Н = 500 * 0,2 = 100(Дж)
равна работе по перемещению бальшого поршня, т.е. Ам = Аб = А = 100Дж:
Аб = Fб * hб = F2 * h = F2 * 0.01
Откуда F2 = 100 / 0,01 = 10 000 Н = 10кН

5.Найти диаметр болта по его прочности на растяжение, если он должен выдержать растягивающее усилие F = 120 кН, а допускаемое напряжение на растяжение для материала болта .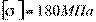

БИЛЕТ 12

БИЛЕТ 13

Условия плавания тел.

Поведение тела, находящегося в жидкости или газе, зависит от соотношения между модулями силы тяжести Fт и архимедовой силы FА, которые действуют на это тело. Возможны следующие три случая:

Fт > FА – тело тонет;

Fт = FА – тело плавает в жидкости или газе;

Fт < FА – тело всплывает до тех пор, пока не начнет плавать.

11. Что такое подъемная сила?

Подъемная сила – разница между силой архимеда и mg

Подъёмная сила — составляющая полной силы давления жидкой или газообразной среды на движущееся в ней тело; направлена перпендикулярно скорости движения тела.

БИЛЕТ 14

1.Уравнение неразрывности. Уравнение Бернулли.

Уравнение неразрывности

За единицу времени через каждое сечение протекает одинаковая масса или объем жидкости

m/t=ρV/t=ρSl/t=ρSѴ=const

Массовый расход = const

SѴ=const

S1Ѵ1=S2Ѵ2 –ур-е неразрывности жидкости (газа)

S1/S2=Ѵ2/Ѵ1

Уравнение Бернулли

Для 2х сечений:

p1+ρV^2/2 +pgh1=p2+ρV^2/2+pgh2

Для каждого сечения

p+ρV^2/2 +pgh=const

где p – статическое давление, ρV^2/2 – динамич давление, pgh – гидростатич давление

Билет

1. Основные характеристики свободных затухающих колебаний. Апериодическое движение.

В следствии диссипации энергии механич колебания затухают.

Основные хар-ки затухающих колебаний:

• Коэф. Затухания β=r/2m; величина обратная коэф затухания наз-ся время релаксации
τ=1/ β

• Частота затухающих колебаний

ω =

• Период затухающ колебаний

T=2π/ ω

• Логарифмич декремент затухания – натуральный логарифм отношения амплитуд, которые по времени отличаются на период Т

λ = ln A(t)/A(t+T)

если β^2< ω0^2, то λ= βТ

Апериодическое движение – процесс, при котором период стремиться к бесконечности

При β^2à ω0^2 (β^2= ω0^2) => ωà0, Tà∞

(15 баллов)

2. Пластичные и хрупкие материалы. Предельное напряжение. Коэффициент запаса прочности. Допускаемые напряжения. (20 баллов)

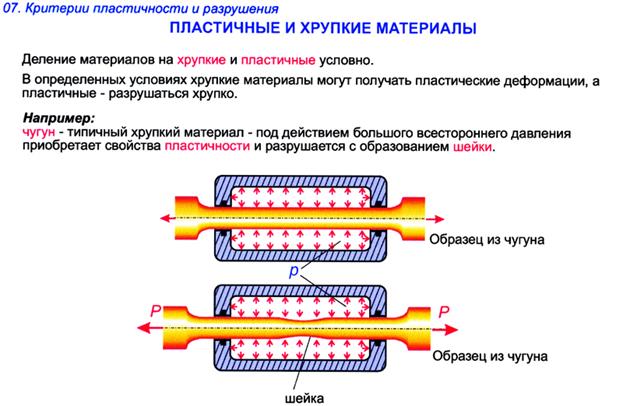
Материалы обладающие очень малой пластичностью, называют хрупкими. У хрупких материалов отсутствует площадка текучести.

Коэффициент запаса - это отношение некоторого предельного напряжения к максимальному напряжению, возникаемому в конструкции.

Максимальное напряжение в конструкции не должно превышать допускаемого напряжения для данного материала определенного с учетом коэффициента запаса для заданных условий работы.

Коэффициент запаса - число большее единицы.

Для того чтобы избежать заметных остаточных деформаций в конструкции за величину некоторого предельного напряжения принимают предел текучести, предел прочности и предел длительной прочности. Для каждой указанной характеристики материала принимают своё значение коэффициента запаса

3. Конструкционные материалы и их свойства. (15 баллов)

Конструкционными материалами называют материалы, из которых изготовляются детали конструкций (машин и сооружений), воспринимающих силовую нагрузку. Определяющими параметрами Конструкционные материалы являются механические свойства, что отличает их от других технических материалов (оптических, изоляционных, смазочных, лакокрасочных, декоративных, абразивных и др.). К основным критериям качества Конструкционные материалы относятся параметры сопротивления внешним нагрузкам: прочность, вязкость, надежность, ресурс и др.

Общие свойства металлов:

- высокая теплопроводность и электропроводность

- повышенная способность к пластической деформации

- хорошая отражательная способность (металлический блеск)

- положительный ТКС

4. Насос, двигатель которого развивает мощность 25 кВт, поднимает 100 м³ нефти на высоту 6 м за 8 мин. Найти КПД установки. Плотность нефти 800 кг/ м³. (25 баллов)

5. Найти диаметр болта по его прочности на растяжение, если он должен выдержать растягивающее усилие F = 120 кН, а допускаемое напряжение на растяжение для материала болта 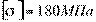. (25 баллов)

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 23

Надежность. Безотказанность и долговечность.

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 25

Коррозия металлов и способы их защиты. Дефект материалов

Де-фекты- отдельные несоответствия продукции нормативным требованиям. Все дефекты в соединениях относятся к двум типам: внешним или внутренним

Дефектом называется каждое отдельное несоответствие продук- ции требованиям, установленным нормативной документацией

Билет №1

Гармонические колебания и их характеристики. Гармонические осцилляторы. Энергия гармонических колебаний.

Колебания – это движения, которые более менее периодически повторяются во времени. Система, совершающая колебания – колебательная система.

Гармонические колебания —колебания, происходящие по закону sin или cos.

Уравнение гармонического колебания имеет вид

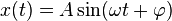
или

,

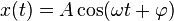где х смещение тела от положения равновесия;

А — амплитуда колебания, т.е. максимальное смещение тела от положения равновесия;

(радиан/с, градус/с) = , циклическая частота гармонических колебаний

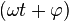(радиан, градус) — полная фаза колебания. Определяет значение x в любой момент времени

0 (радиан, градус) — начальная фаза колебаний

Начальная фаза – определяет значение x в значении t=0, x=

По 2ому закону Ньютона диф.уравнение гармонических колебаний:

Где 𝜔𝑜 = √ 𝑘/𝑚 – собственная частота или частота гармонических колебаний

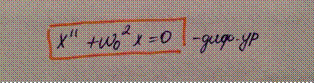
Гармонический осциллятор - это колебательная система, совершающая гармонические колебания.

• Пружинный маятник

F= -kx (Закон Гука)

X<< l малые или упругие деформации

Fсопр= 0

• Механический маятник 𝜔𝑜 = √ 𝑘/ 𝑚 , 𝑇𝑜 = 2𝜋√𝑚/𝑘 зависит от массы тел

• Математический маятник

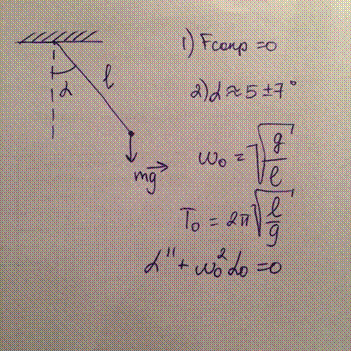
• Физический маятник – твердое тело, совершающее колебания вокруг оси, не проходящей через центр тяжести тела.

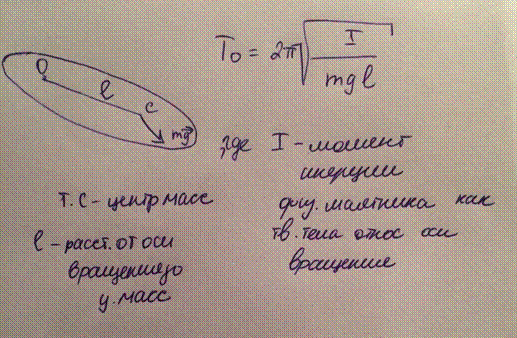
Полная энергия гармонических колебаний равна сумме кинетической энергии и потенциальной энергии