Координатные свойства векторов
1.Каждая координата суммы двух векторов равна сумме соответствующих координат слагаемых векторов.
2.При умножении вектора на число его координаты умножаются на это же число.
Доказательство свойства 1. Пусть в базисе {  1,
1,  2,
2,  3 } имеем
3 } имеем  (
( 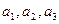 ) и
) и  (
( 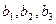 ). Рассмотрим
). Рассмотрим  +
+  = (
= ( 
 1+
1+ 
 2+
2+ 
 3) + (
3) + ( 
 1+
1+ 
 2+
2+ 
 3). Воспользовавшись свойствами сложения векторов и умножения вектора на число, раскрываем скобки и группируем слагаемые по базисным векторам. При этом получим
3). Воспользовавшись свойствами сложения векторов и умножения вектора на число, раскрываем скобки и группируем слагаемые по базисным векторам. При этом получим
 +
+  = (
= (  +
+  )
)  1 + (
1 + (  +
+  )
)  2 + (
2 + (  +
+  )
)  3.
3.
Следовательно,  +
+  (
(  +
+  ,
,  +
+  ,
,  +
+  ).
).
Свойство доказано.
Доказательство свойства 2. Пусть в базисе {  1,
1,  2,
2,  3 } имеем
3 } имеем  (
( 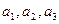 ) и некоторое число l. Если l = 0, то l
) и некоторое число l. Если l = 0, то l  =
= 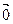 и l
и l  = 0, l
= 0, l  = 0, l
= 0, l  = 0. Свойство 2 справедливо. Если l ¹ 0, то имеем:
= 0. Свойство 2 справедливо. Если l ¹ 0, то имеем:
l  = l (
= l ( 
 1+
1+ 
 2+
2+ 
 3) = l
3) = l 
 1+ l
1+ l 
 2+ l
2+ l 
 3,
3,
то есть
l  ( l
( l  , l
, l  , l
, l  ).
).
Свойство доказано.
Замечание. Доказанное свойство 1 можно доказать и для любого конечного числа слагаемых.
При решении задач, связанных с вычислением длин векторов, величины углов мы будем пользоваться так называемым ортонормированным базисом. Этот базис мы обозначаем { 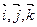 }, и при этом выполняются следующие условия: длины векторов
}, и при этом выполняются следующие условия: длины векторов 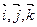 равны единице, сами векторы попарно перпендикулярны и образуют так называемую правую тройку (см. § 6 ).
равны единице, сами векторы попарно перпендикулярны и образуют так называемую правую тройку (см. § 6 ).
Теорема 4. Пусть в базисе { 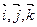 } задан вектор
} задан вектор  (
( 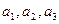 ). Тогда
). Тогда
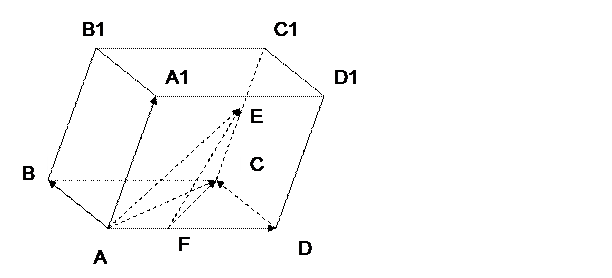
|  | =
| = 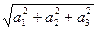 .
.
Доказательство. Согласно теореме 3 имеем единственное разложение
 =
= 
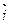 +
+ 
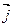 +
+ 
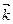 .
.
Выберем произвольно точку О и от нее откладываем векторы: 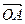 =
= 
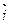 ,
, 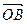 =
= 
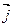 ,
, 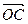 =
= 
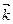 ,
,  =
= 
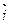 +
+ 
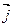 +
+ 
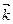 . При этом получим прямоугольный параллелепипед с ребрами ОА, ОВ, ОС и диагональю ОМ, |OA| =|
. При этом получим прямоугольный параллелепипед с ребрами ОА, ОВ, ОС и диагональю ОМ, |OA| =|  |, |OB| =|
|, |OB| =|  |, |ОС| = |
|, |ОС| = |  |,
|,
|OM| =  =
= 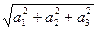 .
.
Теорема доказана.
Пример1.
Дан ортонормированный базис 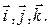 В этом базисе задан вектор
В этом базисе задан вектор 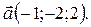 Найти координаты вектора
Найти координаты вектора 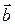 , который коллинеарен вектору
, который коллинеарен вектору 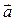 и имеет длину, равную 5.
и имеет длину, равную 5.
Решение. Из коллинеарности векторов 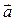 и
и 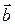 следует, что существует единственное число a ¹ 0, такое что
следует, что существует единственное число a ¹ 0, такое что 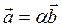 . Так как
. Так как 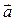 (–1; -2; 2), то координаты вектора
(–1; -2; 2), то координаты вектора 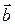 будут соответственно равны
будут соответственно равны  (
( 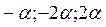 )
)
Из условия, что длина вектора 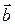 равна 5, получаем следующее равенство:
равна 5, получаем следующее равенство: 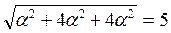 , откуда
, откуда
9 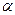 2 =25,
2 =25, 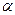 2 =
2 = 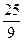 ,
, 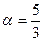 или
или 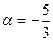 .
.
Последнее означает, что задача имеет два решения:
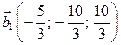 ,
, 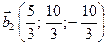 .
.
Пример 2.
Треугольник АВС построен на векторах 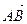 (0,-3,4) и
(0,-3,4) и
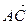 (2,-1,2) в ортонормированном базисе
(2,-1,2) в ортонормированном базисе 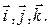 .
.
Найти координаты вектора, параллельного биссектрисе угла ВАС.
Решение.
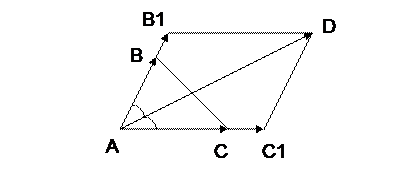

Построим вектора 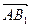 и
и 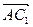 такие, что:
такие, что: 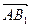
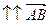 и
и 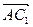
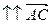 , причем
, причем 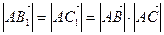 . На данных векторах построим ромб
. На данных векторах построим ромб 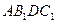 . Диагональ AD ромба
. Диагональ AD ромба 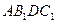 лежит на биссектрисе угла
лежит на биссектрисе угла 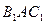 . Следовательно, вектор
. Следовательно, вектор 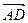 параллелен биссектрисе угла
параллелен биссектрисе угла 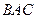 и, при этом,
и, при этом, 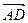 =
= 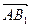 +
+ 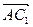 (1).
(1).
Из построения векторов 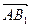 и
и 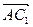 получаем следующие равенства:
получаем следующие равенства:
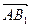 =
= 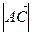
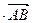 и
и 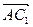 =
= 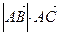 .
.
Из последних равенств и равенства (1) следует, что
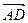 =
= 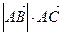 +
+ 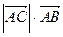 .
.
Так как 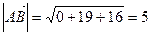 и
и 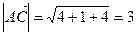 , то
, то
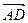 =5
=5 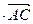 +3
+3 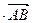 ,
,
откуда
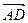 (10;−14;22).
(10;−14;22).
Так как вектор 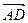 параллелен биссектрисе угла
параллелен биссектрисе угла 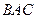 , то и вектор
, то и вектор 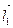 (5,−7,11) будет параллельным этой биссектрисе. Любой другой вектор
(5,−7,11) будет параллельным этой биссектрисе. Любой другой вектор 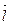 , параллельный биссектрисе угла
, параллельный биссектрисе угла 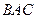 , будет иметь координаты
, будет иметь координаты
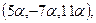 где
где 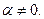
Таким образом, решением является вектор 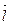
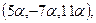 где
где 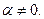
Пример 3.
Дан параллелепипед 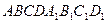 . Точки
. Точки 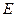 и
и 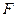 - середины соответственно ребер
- середины соответственно ребер 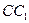 и
и 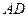 . В качестве базисных векторов взяты векторы
. В качестве базисных векторов взяты векторы 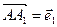 ,
, 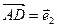 ,
, 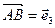 . Найти координаты векторов
. Найти координаты векторов 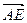 ,
, 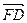 и
и 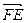 в данном базисе.
в данном базисе.
Решение.

1) 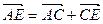 (1),
(1), 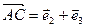 (2),
(2),
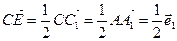 , откуда
, откуда 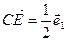 (3).
(3).
Из равенств (1), (2), (3) следует, что 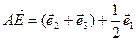 .
.
Используя свойства коммутативности и ассоциативности операции сложения векторов, получаем следующее равенство: 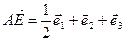 .
.
Следовательно, 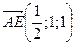 .
.
2) 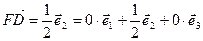 , откуда получаем:
, откуда получаем: 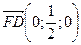 .
.
3) 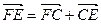 (1),
(1), 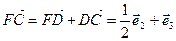 , откуда
, откуда 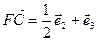 (2),
(2),
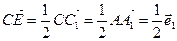 , откуда
, откуда 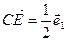 (3).
(3).
Из равенств (1), (2) и (3) имеем: 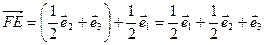 .
.
Следовательно, 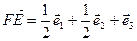 , откуда
, откуда 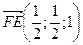 .
.
