Координаты вектора. Векторные
пространства V1, V2, V3
Обозначим множество всех векторов V3. Выберем ненулевой вектор  и рассмотрим все векторы коллинеарные с
и рассмотрим все векторы коллинеарные с  . Обозначим полученное множество векторов V1. Выберем в пространстве V3 два неколлинеарных вектора
. Обозначим полученное множество векторов V1. Выберем в пространстве V3 два неколлинеарных вектора  1 и
1 и  2 и рассмотрим все векторы пространства компланарные с
2 и рассмотрим все векторы пространства компланарные с  1 и
1 и  2. Обозначим полученное множество векторов V2.
2. Обозначим полученное множество векторов V2.
Из построения следует, что в пространстве V3 существует множество подпространств V1 и V2.
Рассмотрим пространство V1. Назовем базисом пространства V1 ненулевой вектор этого пространства. Обозначим его  . Рассмотрим произвольный вектор
. Рассмотрим произвольный вектор  Î V1. Докажем, что всегда существует единственное число х, такое, что
Î V1. Докажем, что всегда существует единственное число х, такое, что  = х
= х  .
.
Теорема 1. Пусть дано пространство V1 и ненулевой вектор  Î V1. Тогда для любого вектора
Î V1. Тогда для любого вектора  Î V1
Î V1  существует единственное число х, такое, что
существует единственное число х, такое, что  = х
= х  .
.
Доказательство. Действительно, если  =
= 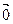 , то х = 0. Если
, то х = 0. Если  ¹
¹ 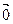 , то полагаем х =
, то полагаем х = 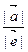 , если
, если 
 и х = -
и х = - 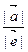 , если
, если  ¯
¯  . Покажем, что рассматриваемое равенство верно, то есть
. Покажем, что рассматриваемое равенство верно, то есть  =
= 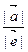
 , если
, если 
 и
и  = -
= - 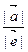
 , если
, если  ¯
¯  . Действительно,
. Действительно,
|± 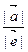
 | =
| = 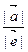 |
|  | = |
| = |  | и |
| и |  | =|
| =|  |.
|.
Равенство длин рассматриваемых векторов доказано. Сонаправленность этих векторов очевидна. Следовательно, существование числа х доказано.
Докажем единственность разложения. Предположим, что верны два равенства  = х
= х  и
и  = х1
= х1  . Вычтем из первого равенства второе. Получим:
. Вычтем из первого равенства второе. Получим:
(х – х1)  =
= 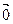 .
.
Если выражение в скобке не равно нулю, то получим  =
= 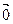 , что противоречит условию. Следовательно, х = х1.
, что противоречит условию. Следовательно, х = х1.
Теорема доказана.
Число х называем координатой вектора  в базисе {
в базисе {  } и обозначаем
} и обозначаем  (х).
(х).
Следствие. Любые два коллинеарных вектора образуют линейно зависимую систему векторов.
Рассмотрим пространство V2. Назовем базисом пространства V2 пару неколлинеарных векторов этого пространства. Обозначим его  1,
1,  2 . Рассмотрим произвольный вектор
2 . Рассмотрим произвольный вектор  Î V2. Докажем, что всегда существуют единственная пара чисел х, у такая, что
Î V2. Докажем, что всегда существуют единственная пара чисел х, у такая, что  = х
= х  1 + у
1 + у  2.
2.
Теорема 2. Пусть дано пространство V2 и базис  1,
1,  2. Тогда для любого вектора
2. Тогда для любого вектора  Î V2
Î V2  существует единственная пара чисел х, у такая, что
существует единственная пара чисел х, у такая, что  = х
= х  1 + у
1 + у  2.
2.
Доказательство. Выберем произвольно точку О и от нее откладываем векторы: 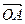 =
=  1,
1, 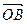 =
=  2 и
2 и  =
=  . При этом полученные точки О, А, В и М лежат в одной плоскости. Построим параллелограмм с диагональю ОМ и смежными сторонами, лежащими на прямых ОА и ОВ. Обозначим построенный параллелограмм ОА′МВ¢.
. При этом полученные точки О, А, В и М лежат в одной плоскости. Построим параллелограмм с диагональю ОМ и смежными сторонами, лежащими на прямых ОА и ОВ. Обозначим построенный параллелограмм ОА′МВ¢.


При этом имеем :
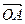 ¢ +
¢ + 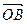 ¢=
¢=  ,
, 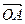 ¢= х
¢= х  1,
1, 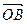 ¢ = у
¢ = у  2 ( теорема 1) и, соответственно,
2 ( теорема 1) и, соответственно,
 = х
= х  1 + у
1 + у  2.
2.
Докажем единственность разложения. Предположим, что верны два равенства  = х
= х  1 + у
1 + у  2 и
2 и  = х1
= х1  1 + у1
1 + у1  2. Вычтем из первого равенства второе. Получим:
2. Вычтем из первого равенства второе. Получим:
(х – х1)  1 +(у – у1)
1 +(у – у1)  2 =
2 = 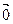 .
.
Если хотя бы одно выражение в скобках не равно нулю, например, у – у1 ¹ 0, то получим
 2 = -
2 = - 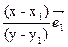 .
.
Получили, что векторы  1 и
1 и  2 - коллинеарные, что противоречит условию. Следовательно, х = х1, у = у1. Теорема доказана..
2 - коллинеарные, что противоречит условию. Следовательно, х = х1, у = у1. Теорема доказана..
Числа х, у называем координатами вектора  в базисе {
в базисе {  1,
1,  2} и обозначаем
2} и обозначаем  ( х, у).
( х, у).
Следствие. Любая тройка компланарных векторов образует линейно зависимую систему векторов и наоборот.
Рассмотрим пространство V3. Назовем базисом пространства V3 тройку некомпланарных векторов этого пространства. Обозначим ее  1,
1,  2,
2,  3 . Рассмотрим произвольный вектор
3 . Рассмотрим произвольный вектор  Î V3. Докажем, что всегда существуют единственная тройка чисел х, у, z такая, что
Î V3. Докажем, что всегда существуют единственная тройка чисел х, у, z такая, что  = х
= х  1 + у
1 + у  2 +z
2 +z  3.
3.
Теорема 3. Пусть дано пространство V3 и базис 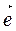 1,
1,  2,
2,  3. Тогда для любого вектора
3. Тогда для любого вектора  Î V3
Î V3  существует единственная тройка чисел х, у, z такая, что
существует единственная тройка чисел х, у, z такая, что  = х
= х  1 + у
1 + у  2 +z
2 +z  3.
3.
Доказательство. Выберем произвольно точку О и от нее откладываем векторы: 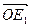 =
=  1,
1, 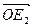 =
=  2,
2, 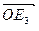 =
=  3 и
3 и 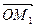 =
=  . Построим параллелепипед с диагональю ОМ1 и смежными сторонами, лежащими на прямых ОЕ1, ОЕ2 и ОЕ3. Обозначим построенный параллелепипед ОАМВО1А1М1В1. При этом имеем :
. Построим параллелепипед с диагональю ОМ1 и смежными сторонами, лежащими на прямых ОЕ1, ОЕ2 и ОЕ3. Обозначим построенный параллелепипед ОАМВО1А1М1В1. При этом имеем :

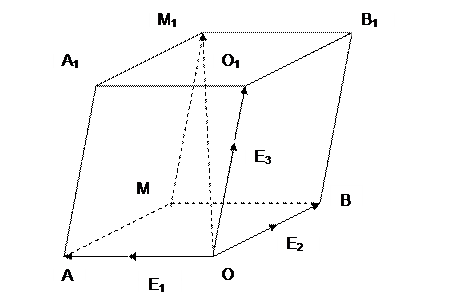

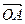 +
+ 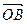 +
+ 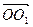 =
= 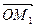 ,
, 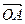 = х
= х  1,
1, 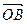 = у
= у  2 ,
2 , 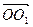 = z
= z  3 ( теорема 1) и, соответственно,
3 ( теорема 1) и, соответственно,
 = х
= х  1 + у
1 + у  2 +z
2 +z  3.
3.
Докажем единственность разложения. Предположим, что верны два равенства  = х
= х  1 + у
1 + у  2 +z
2 +z  3 и
3 и  = х1
= х1  1 + у1
1 + у1  2 +z1
2 +z1  3 . Вычтем из первого равенства второе. Получим:
3 . Вычтем из первого равенства второе. Получим:
(х – х1)  1 +(у – у1)
1 +(у – у1)  2 + (z - z1)
2 + (z - z1)  3 =
3 = 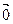 .
.
Если хотя бы одно выражение в скобках не равно нулю, например, у – у1 ¹ 0, то получим
 2 = -
2 = - 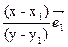 -
- 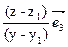
Получили, что векторы  1 ,
1 ,  2 и
2 и  3 - линейно зависимы, а, следовательно, компланарные, что противоречит условию.
3 - линейно зависимы, а, следовательно, компланарные, что противоречит условию.
Поэтому, х = х1, у = у1 = z – z1, Теорема доказана.
Числа х, у, z называем координатами вектора  в базисе {
в базисе {  1,
1,  2,
2,  3 } и обозначаем
3 } и обозначаем  ( х, у, z).
( х, у, z).
