Выражение мощности через симметричные составляющие
Комплекс полной мощности в трехфазной цепи
 . | (14) |
Для фазных напряжений имеем
 | (15) |
Учитывая, что комплекс, сопряженный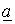 
, равен 
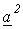и наоборот, для сопряженных комплексов токов запишем:
 | (16) |
Подставляя (15) и (16) в (14), после соответствующих преобразований получим
.
Отсюда
и
,
где 
- разности фаз соответствующих симметричных составляющих напряжений и токов.
Литература
- Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
- Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
Контрольные вопросы и задачи
- В каких случаях целесообразно применение теоремы об активном двухполюснике для симмметричных составляющих?
- Как рассчитываются эквивалентные параметры симметричной цепи, к которой подключается локальная несимметричная нагрузка?
- В чем заключаются особенности расчета входного сопротивления нулевой последовательности?
- Какова последовательность анализа трехфазной цепи с использованием теоремы об активном двухполюснике для симметричных составляющих?
- Определить напряжения
и 
в цепи на рис. 3, если фазная ЭДС 
, а сопротивления прямой и обратной последовательностей равны: 
.
Ответ: 
.
- Фазы А и С симметричного трехфазного источника замкнуты накоротко. Определить ток короткого замыкания, если
, а сопротивления прямой и обратной последовательностей 
.
Ответ: 
.
Как было показано ранее, одним из важнейших преимуществ многофазных систем является получение вращающегося магнитного поля с помощью неподвижных катушек, на чем основана работа двигателей переменного тока. Рассмотрение этого вопроса начнем с анализа магнитного поля катушки с синусоидальным током. Магнитное поле катушки с синусоидальным током При пропускании по обмотке катушки синусоидального тока она создает  магнитное поле, вектор индукции которого изменяется (пульсирует) вдоль этой катушки также по синусоидальному закону Мгновенная ориентация вектора магнитной индукции в пространстве зависит от намотки катушки и мгновенного направления тока в ней и определяется по правилу правого буравчика. Так для случая, показанного на рис. 1, вектор магнитной индукции направлен по оси катушки вверх. Через полпериода, когда при том же модуле ток изменит свой знак на противоположный, вектор магнитной индукции при той же абсолютной величине поменяет свою ориентацию в пространстве на 1800. С учетом вышесказанного магнитное поле катушки с синусоидальным током называют пульсирующим. Круговое вращающееся магнитное поле двух- и трехфазной обмоток Круговым вращающимся магнитным полем называется поле, вектор магнитной индукции которого, не изменяясь по модулю, вращается в пространстве с постоянной угловой частотой. Для создания кругового вращающегося поля необходимо выполнение двух условий:
 и  , характеризующие эти поля, направлены вдоль осей соответствующих катушек, а их амплитуды изменяются также по гармоническому закону. Если ток в катушке В отстает от тока в катушке А на 900 (см. рис. 2,б), то  . Найдем проекции результирующего вектора магнитной индукции  на оси x и y декартовой системы координат, связанной с осями катушек:   Модуль результирующего вектора магнитной индукции в соответствии с рис. 2,в равен
при этом для тангенса угла a , образованного этим вектором с осью абсцисс, можно записать
откуда
Полученные соотношения (1) и (2) показывают, что вектор результирующего магнитного поля неизменен по модулю и вращается в пространстве с постоянной угловой частотой Покажем, что симметричная трехфазная система катушек (см. рис. 3,а) также позволяет получить круговое вращающееся магнитное поле. Каждая из катушек А, В и С при пропускании по ним гармонических токов создает пульсирующее магнитное поле. Векторная диаграмма в пространстве для этих полей представлена на рис. 3,б. Для проекций результирующего вектора магнитной индукции на
оси декартовой системы координат, ось y у которой совмещена с магнитной осью фазы А, можно записать
Приведенные соотношения учитывают пространственное расположение катушек, но они также питаются трехфазной системой токов с временным сдвигом по фазе на 1200. Поэтому для мгновенных значений индукций катушек имеют место соотношения
Подставив эти выражения в (3) и (4), получим:
В соответствии с (5) и (6) и рис. 2,в для модуля вектора магнитной индукции результирующего поля трех катушек с током можно записать:
а сам вектор
откуда
Таким образом, и в данном случае имеет место неизменный по модулю вектор магнитной индукции, вращающийся в пространстве с постоянной угловой частотой Наши рекомендации |
, 
,
. 
, описывая окружность, что соответствует круговому вращающемуся полю.
; 
. 
; 
; 
.
; 
,
,