Ii. кручение стержней круглого сечения.
Введение.
Индивидуальное задание студент выбирает, в соответствии с номером зачетной книжки, по двум последним цифрам: «первая» - номер расчетной схемы, «вторая» - номер условия.
Пример: З.К. № ОЗ-ТЗ-1-164; - «6»- номер расчетной схемы, - «4»- номер условия.
Задачи к контрольным заданиям. Статика.
Задача С1
Жесткая рама, расположенная в вертикальной плоскости (рис. С-1.0 - С1.9, табл. С-1), закреплена в точке А шарнирно, а в точке В прикреплена или к невесомому стержню с шарнирами на концах, или к шарнирной опоре на катках.
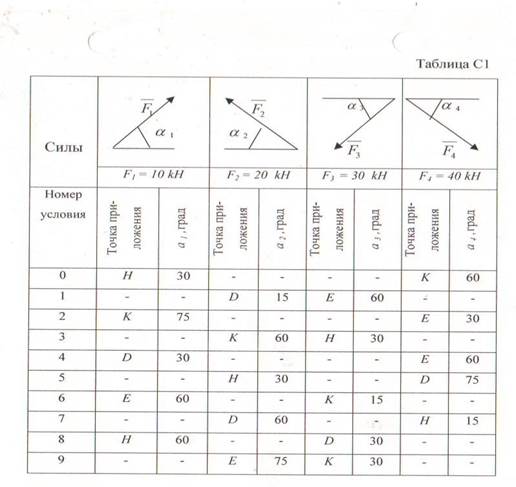
В точке С к раме привязан трос, перекинутый через блок и несущий на конце груз весом Р = 25 кН. На раму действует пара сил с моментом М= 100 кН-м и две силы, значения, направления и точки приложения которых указаны в таблице (например, в условиях №1 на раму действует сила F2 под углом 15° к горизонтальной оси, приложенная в точке D, и сила F3 под углом
60° к горизонтальной оси, приложенная в точке Е, и т.д.).
Определить реакции связей в точках А,В, вызываемые действующими нагрузками. При окончательных расчетах принять а = 0,5 м.
Указания. Задача С1 - на равновесие тела под действием произвольной плоскости системы сил. При ее решении учесть, что натяжения обеих ветвей нити, перекинутой через блок, когда трением пренебрегают, будут одинаковыми. Уравнение моментов будет простым (содержать меньше неизвестных), если брать моменты относительно точки, где пересекаются линии действия
двух реакций связей. При вычислении момента силы f часто удобно разложить ее на составляющие f и f", для которых плечи легко определяются, и воспользоваться теоремой Вариньона: тогда
т0 (f)= т0 (f )+т0 (f" ).
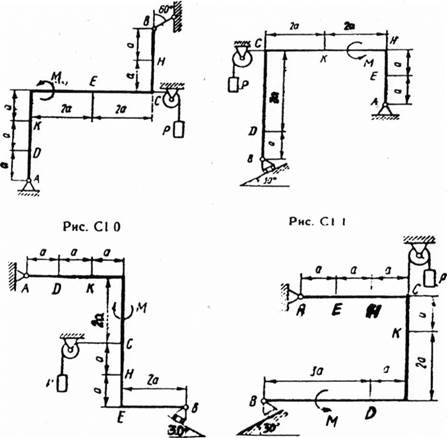
Рис.С 1.2 Рис. С 1.3
.
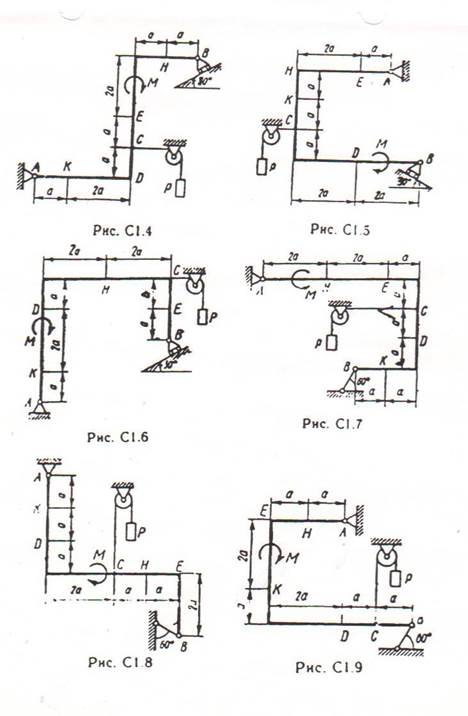
Кинематика.
Задача К1.
Под номером К1 помещены две задачи К1а и К1 б, которые надо решить.
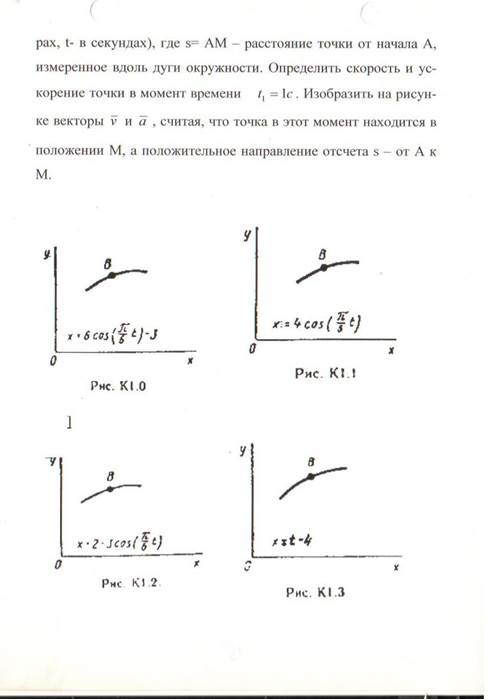
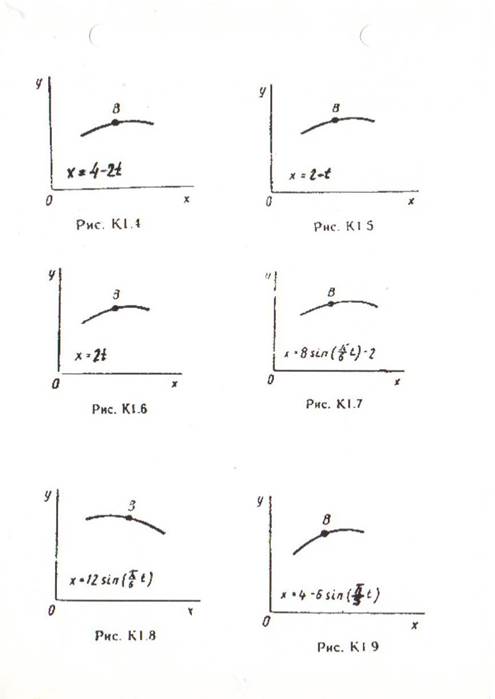
Задача К 1а. Точка В движется в плоскости ху (рис. К1.0-К1.9, табл. К1; траектория точки на рисунках показана условно).
Закон движения точки задан уравнениями:
х = f1(t), y = f2(t),
где х и у выражены в сантиметрах, t - в секундах.
Найти уравнение траектории точки; для момента времени t1 = 1с определить скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.
Зависимость х = f1(t)указана непосредственно на рисунках, а зависимость
у = f2(t) дана в табл. К1 (для рис. 0-2 в столбце 2, для рис. 3-6 в столбце 3, для рис. 7-9 в столбце 4).
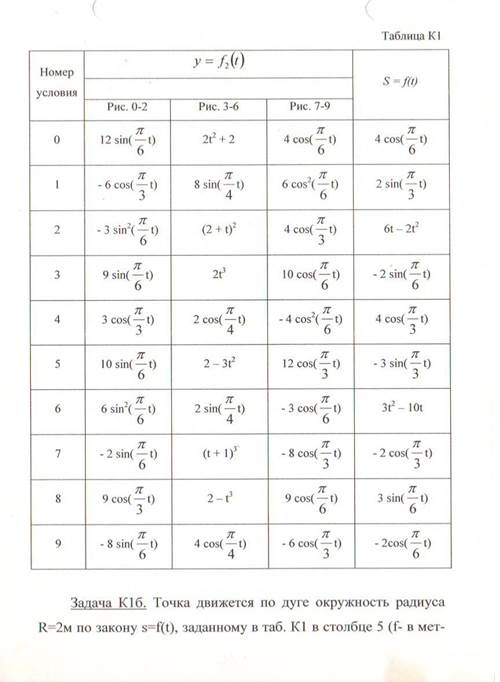
Указания. Задача К1 относится к кинематике точки и решается с помощью формул, по которым определяются скорость и ускорение точки в декартовых координатах (координатный способ задания движения точки), а также формул, по которым определяются скорость, касательное и нормальное ускорения точки при естественном способе задания ее движения.
В задаче все искомые величины нужно определить только для момента времени t1, = 1с. В некоторых вариантах задачи К1а при определении траектории или при последующих расчетах (для их упрощения) следует учесть известные из тригонометрии формулы:
cos 2а = 1 - 2 sin2 а = 2 cos2 а -1;
sin 2а = 2sin а cos а.
I. Растяжение и сжатие.
Задание 1
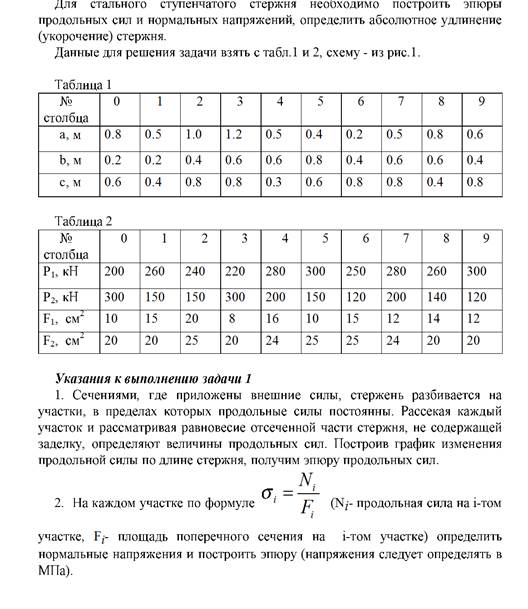
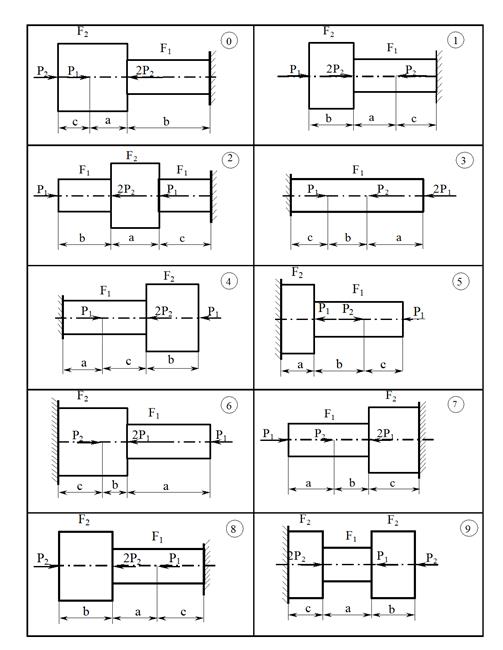Схема 1.
З а д а н и е 2
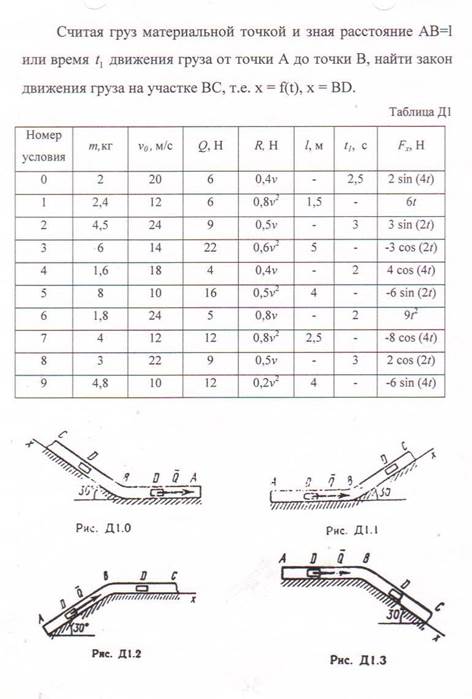
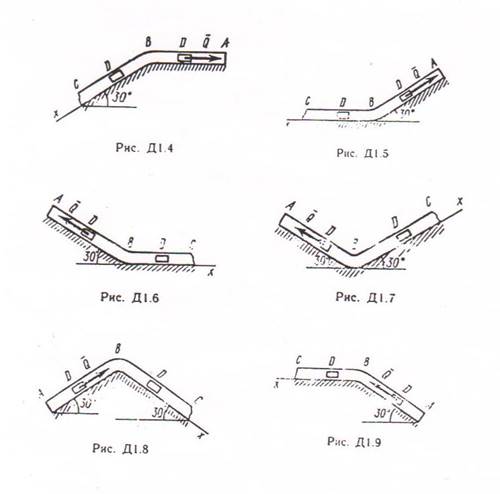
К стальному валу приложены три известных момента: Т1, Т2, Т3 Требуется:
1) из условия равновесия вала найти значение момента Х (сопротивлением опор пренебречь);
2) построить эпюру крутящих моментов;
3) из расчета на прочность определить диаметр вала;
4) из расчета на прочность подобрать вал кольцевого поперечного сечения при заданном отношении внутреннего диаметра d к наружному D;
5) выбрать вал с меньшей площадью поперечного сечения;
6) для выбранного вала построить эпюру углов закручивания, вычислить наибольший относительный угол закручивания θ и сравнить его с допускаемым [θ] = 1 град/м.
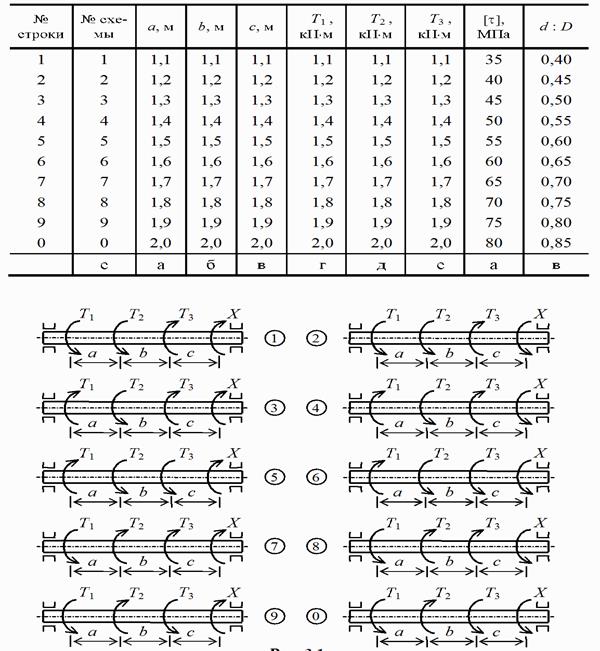
Данные взять из табл.
При определении диаметра сплошного вала и наружного диаметра вала кольцевого сечения полученные значения округляют по ГОСТ 6636–69 до ближайшего значения из ряда Rа40: 10; 10,5; 11; 11,5; 12; 13; 14; 15; 16; 17; 18; 19; 20; 21; 22; 24; 25; 26; 28; 30; 32; 34; 36; 38; 40; 42; 45; 48; 50; 52; 55; 60; 63; 65; 70; 75; 80; 85; 90; 95; 100; 105; 110; 120; 125; 130; 140; 150; 160 мм.
Задание 3
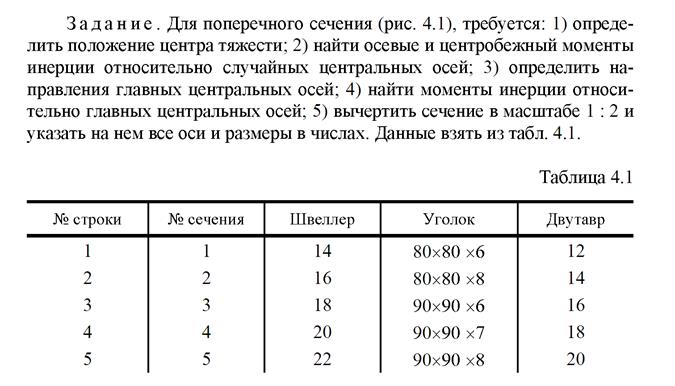
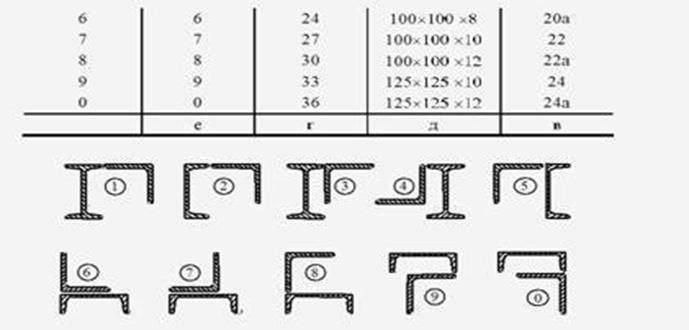
Рис.4.1
Задача 4.1
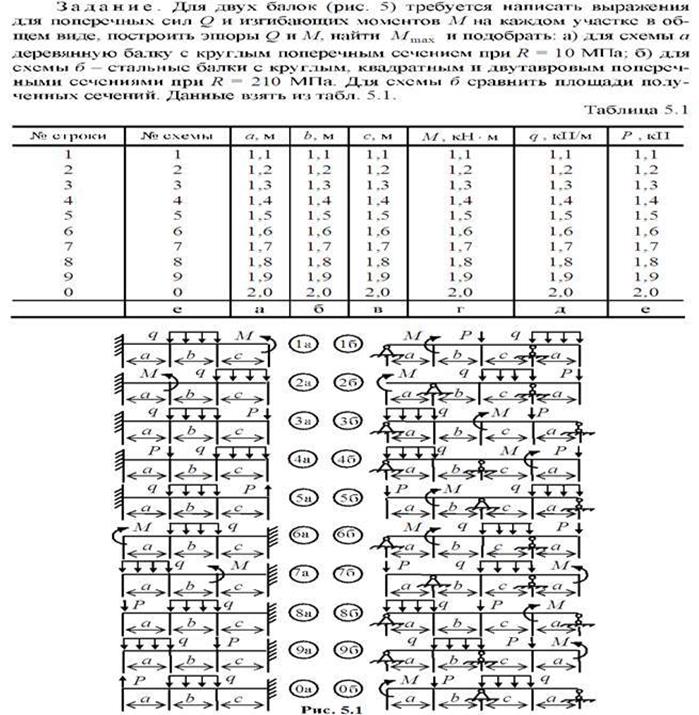
Таблица 5.1
Исходные данные к заданию 5
| № В варианта | a, | Nв, кВт | nв, об/мин | Действующие силы |
| м | ||||
| 0,1 | A1,R1, R3, F1, F4 | |||
| 0,2 | A1,R2, R4, F2, F3 | |||
| 0,3 | A2,R2, R3, F1, F4 | |||
| 0,2 | A2,R1, R4, F2, F3 | |||
| 0,3 | A1,R2, R3, F1, F4 | |||
| 0,1 | A2,R2, R4, F2, F3 | |||
| 0,3 | A1,R1, R3, F1, F4 | |||
| 0,2 | A2,R2, R4, F2, F3 | |||
| 0,3 | A1,R1, R3, F1, F4 | |||
| 0,1 | A2,R2, R4, F2, F3 |
Таблица 5.2.
Исходные данные к задаче 5
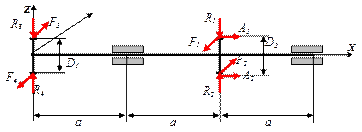
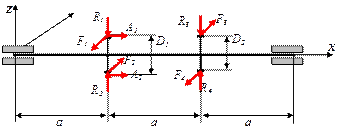
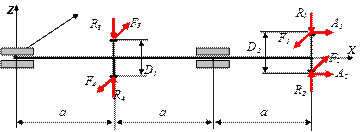
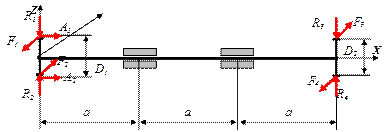
| № А варианта | D1 , мм | D2 , мм | Расчетная схема вала |
 | |||
 | |||
 | |||
 | |||
 | |||
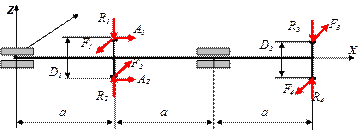Рекомендуемый порядок выполнения задания № 5:
- Нарисовать в масштабе расчетную схему вала по индивидуальным данным.
- По заданной мощности Nв и числу оборотов nв вала определить действующие нагрузки, используя заданные соотношения.
- По внешним нагрузкам определить реакции в подшипниковых узлах. При этом реакциями от крутящего момента пренебрегают.
- Используя метод сечений на каждом расчетном участке определить и построить в масштабе эпюры продольной силы N, крутящего Mk = Mx и изгибающих моментов Mz , My.
- Определить опасные сечения вала.
- Определить величину диаметра d вала по условию III теории прочности.
Введение.
Индивидуальное задание студент выбирает, в соответствии с номером зачетной книжки, по двум последним цифрам: «первая» - номер расчетной схемы, «вторая» - номер условия.
Пример: З.К. № ОЗ-ТЗ-1-164; - «6»- номер расчетной схемы, - «4»- номер условия.
Задачи к контрольным заданиям. Статика.
Задача С1
Жесткая рама, расположенная в вертикальной плоскости (рис. С-1.0 - С1.9, табл. С-1), закреплена в точке А шарнирно, а в точке В прикреплена или к невесомому стержню с шарнирами на концах, или к шарнирной опоре на катках.
В точке С к раме привязан трос, перекинутый через блок и несущий на конце груз весом Р = 25 кН. На раму действует пара сил с моментом М= 100 кН-м и две силы, значения, направления и точки приложения которых указаны в таблице (например, в условиях №1 на раму действует сила F2 под углом 15° к горизонтальной оси, приложенная в точке D, и сила F3 под углом
60° к горизонтальной оси, приложенная в точке Е, и т.д.).
Определить реакции связей в точках А,В, вызываемые действующими нагрузками. При окончательных расчетах принять а = 0,5 м.
Указания. Задача С1 - на равновесие тела под действием произвольной плоскости системы сил. При ее решении учесть, что натяжения обеих ветвей нити, перекинутой через блок, когда трением пренебрегают, будут одинаковыми. Уравнение моментов будет простым (содержать меньше неизвестных), если брать моменты относительно точки, где пересекаются линии действия
двух реакций связей. При вычислении момента силы f часто удобно разложить ее на составляющие f и f", для которых плечи легко определяются, и воспользоваться теоремой Вариньона: тогда
т0 (f)= т0 (f )+т0 (f" ).
Рис.С 1.2 Рис. С 1.3
.
Кинематика.
Задача К1.
Под номером К1 помещены две задачи К1а и К1 б, которые надо решить.
Задача К 1а. Точка В движется в плоскости ху (рис. К1.0-К1.9, табл. К1; траектория точки на рисунках показана условно).
Закон движения точки задан уравнениями:
х = f1(t), y = f2(t),
где х и у выражены в сантиметрах, t - в секундах.
Найти уравнение траектории точки; для момента времени t1 = 1с определить скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.
Зависимость х = f1(t)указана непосредственно на рисунках, а зависимость
у = f2(t) дана в табл. К1 (для рис. 0-2 в столбце 2, для рис. 3-6 в столбце 3, для рис. 7-9 в столбце 4).
Указания. Задача К1 относится к кинематике точки и решается с помощью формул, по которым определяются скорость и ускорение точки в декартовых координатах (координатный способ задания движения точки), а также формул, по которым определяются скорость, касательное и нормальное ускорения точки при естественном способе задания ее движения.
В задаче все искомые величины нужно определить только для момента времени t1, = 1с. В некоторых вариантах задачи К1а при определении траектории или при последующих расчетах (для их упрощения) следует учесть известные из тригонометрии формулы:
cos 2а = 1 - 2 sin2 а = 2 cos2 а -1;
sin 2а = 2sin а cos а.
I. Растяжение и сжатие.
Задание 1
Схема 1.
II. КРУЧЕНИЕ СТЕРЖНЕЙ КРУГЛОГО СЕЧЕНИЯ.
З а д а н и е 2
К стальному валу приложены три известных момента: Т1, Т2, Т3 Требуется:
1) из условия равновесия вала найти значение момента Х (сопротивлением опор пренебречь);
2) построить эпюру крутящих моментов;
3) из расчета на прочность определить диаметр вала;
4) из расчета на прочность подобрать вал кольцевого поперечного сечения при заданном отношении внутреннего диаметра d к наружному D;
5) выбрать вал с меньшей площадью поперечного сечения;
6) для выбранного вала построить эпюру углов закручивания, вычислить наибольший относительный угол закручивания θ и сравнить его с допускаемым [θ] = 1 град/м.
Данные взять из табл.
При определении диаметра сплошного вала и наружного диаметра вала кольцевого сечения полученные значения округляют по ГОСТ 6636–69 до ближайшего значения из ряда Rа40: 10; 10,5; 11; 11,5; 12; 13; 14; 15; 16; 17; 18; 19; 20; 21; 22; 24; 25; 26; 28; 30; 32; 34; 36; 38; 40; 42; 45; 48; 50; 52; 55; 60; 63; 65; 70; 75; 80; 85; 90; 95; 100; 105; 110; 120; 125; 130; 140; 150; 160 мм.