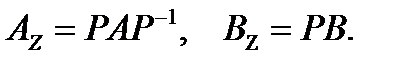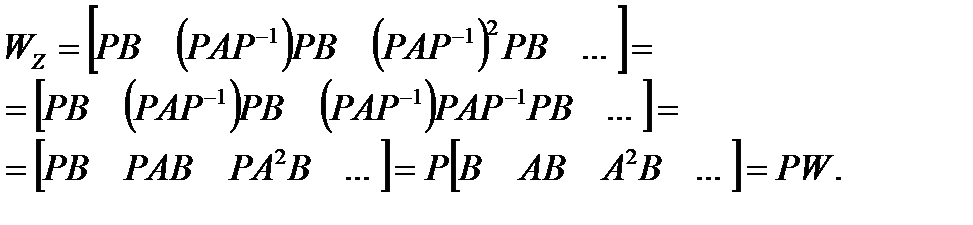Уравнения состояния и сигнальный граф

С помощью сигнальных графов и формулы Мейсона можно переходить от уравнений состояния к ПФ и наоборот.

Пусть X(s) и Y(s) – входная и выходная переменные системы. Тогда для вычисления ПФ системы управления по ее графу можно воспользоваться формулой Мейсона:

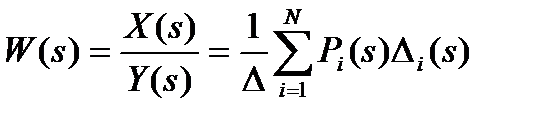
где P_i(s) – передаточная функция i-го отдельного прямого пути от X(s) до Y(s), вычисленная как произведение передаточных функций дуг, входящих в этот путь;

D(s) – определитель графа.

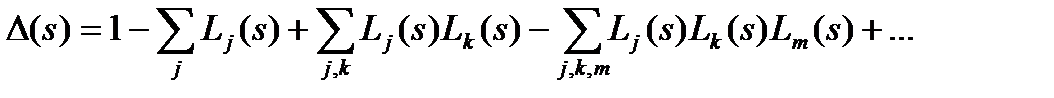
где L_j(s) – ПФ j-го замкнутого контура, равная произведению ПФ дуг, входящих в этот контур;

L_j(s)L_k(s) – произведение ПФ пары (j-го и k-го) замкнутых контуров, не касающихся ни дугами, ни вершинами, суммирование осуществляется по всем парам не касающихся контуров;

L_j(s)L_k(s)L_m(s) – произведение тройки (j-го, k-го и m-го) не касающихся контуров, суммирование производится по всем тройкам не касающихся контуров.

D_i(s) – дополнительный множитель для i- го пути равен определителю графа, в котором приравнены нулю коэффициенты передачи контуров, касающихся этого пути.

Пример 1.15. Рассмотрим еще раз уравнения состояния RLC – цепи:

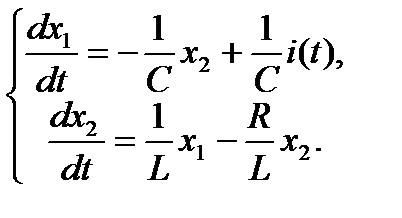
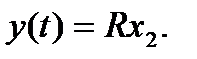
Им соответствует сигнальный граф, показанный на рис. 1.12.

1/s

I(s)

R

1/C

–R/L

1/s

–1/C

1/L

x2

x1

Y(s)

Рис. 1.12. Сигнальный граф для уравнений состояния

Граф содержит один путь и два касающихся контура:

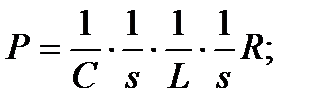
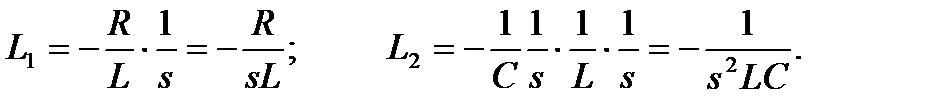
По формуле Мейсона ПФ оказывается равна:

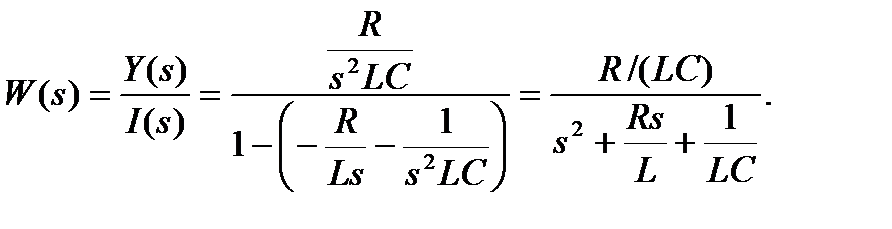
Рассмотрим далее ПФ вида

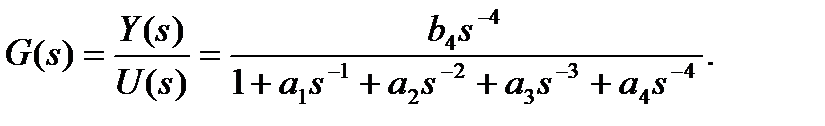
Если считать, что это формула Мейсона, то числитель соответствует единственному прямому пути в графе, а знаменатель является определителем графа, содержащего четыре касающихся контура. Таким образом, получаем граф, представленный на рис. 1.13.

1/s

U(s)

b4

1/s

x4

x1

Y(s)

-a4

x3

1/s

1/s

x2

-a3

-a2

-a1

Рис. 1.13. Сигнальный граф для передаточной функции

Рассмотрим теперь ПФ более общего вида

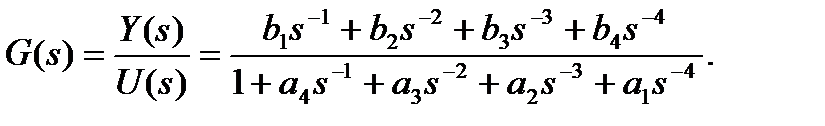
Знаменатель здесь такой же как в предыдущем примере, а числитель можно рассматривать как сумму 4-х прямых путей. Получаем граф, показанный на рис. 1.14.

1/s

U(s)

b1

1/s

x4

Y(s)

-a1

x2

1/s

1/s

x3

-a2

-a3

-a4

b4

b3

b2

x1

Рис. 1.14. Сигнальный граф для ПФ общего вида

Для графа на рис. 1.14 можно записать

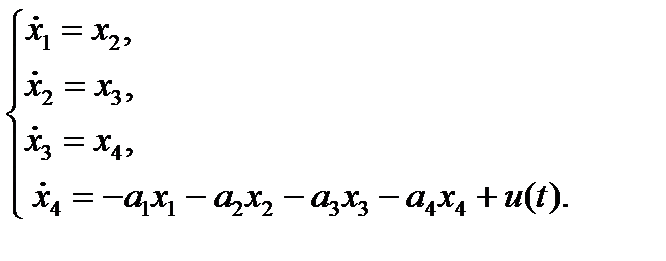
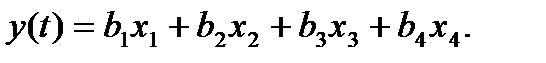
В матричной форме

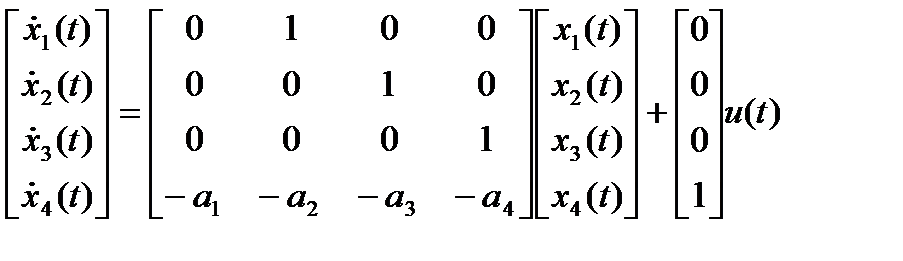
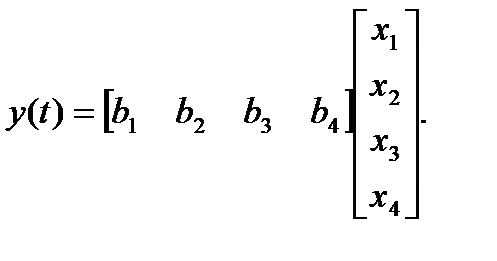
1.6. Преобразование подобия

Для одной и той же системы можно предложить неограниченное количество троек матриц A, B, C,каждой из которых будет соответствовать модель в переменных состояния. Выбор той или иной модели зависит от конкретных обстоятельств:

Преобразованиями подобия называются такие преобразования, которые изменяют внутреннюю структуру системы (модель состояния), но не изменяют соотношение между входом и выходом (передаточную функцию системы).

Для системы с вектором состояния X рассмотрим невырожденное линейное преобразование

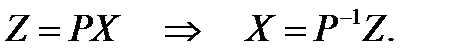
где Z – вектор состояния системы в новом базисе, P – произвольная невырожденная матрица (определитель не равен нулю).

Для перехода к новому базису подставим новый вектор состояния

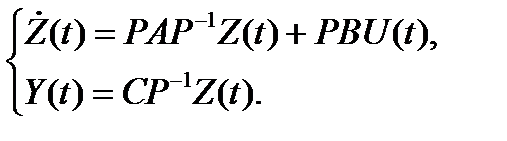или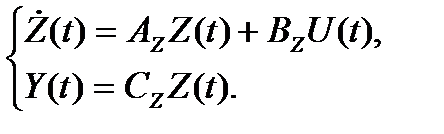

где

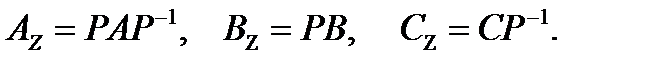
Если в системе имеется ненулевая матрица D, то D_z = D.

Пример 1.15.Пусть дана система, матрицы A, B и C которой имеют вид:

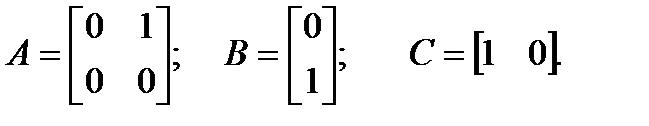
Запишем уравнения состояния

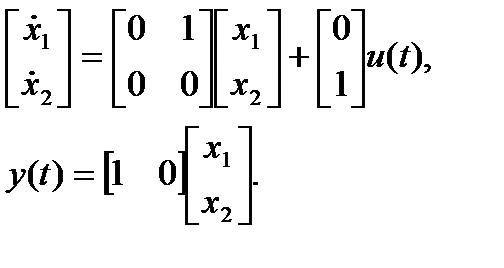
Этим уравнениям соответствует структурная схема, приведенная на рис.1.15.

x1 = y(t)

x2

u(t)

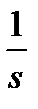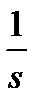Рис. 1.15. Система из двух интеграторов

Очевидно, что для этой схемы

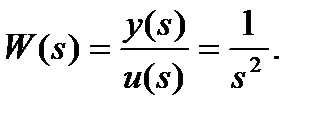
Рассмотрим невырожденное преобразование координат, заданное матрицей P:

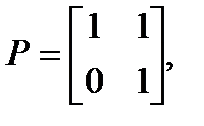
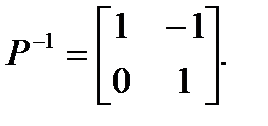
Преобразованные матрицы в новой системе координат имеют вид:

,

.

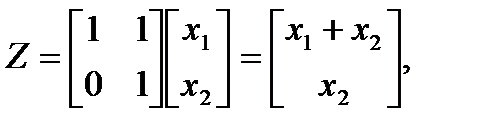
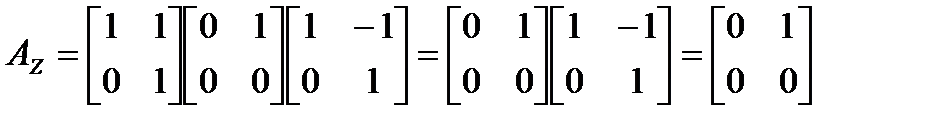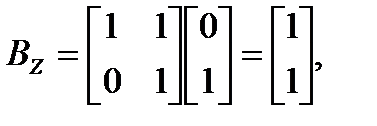
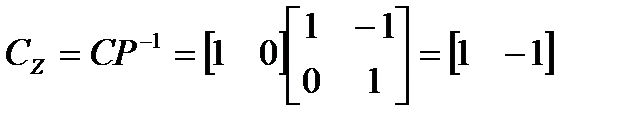Таким образом,

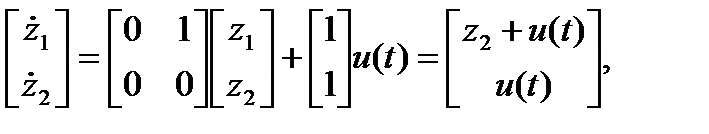
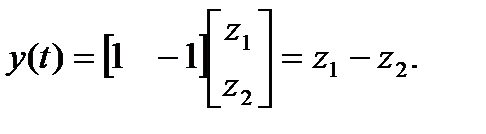
Полученным уравнениям состояния соответствует структура, показанная на рис. 1.16.

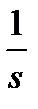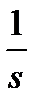z1

u(t)

z2

y(t)

Рис. 1.16. Преобразованная система из двух интеграторов

Для проверки построим передаточную функцию:

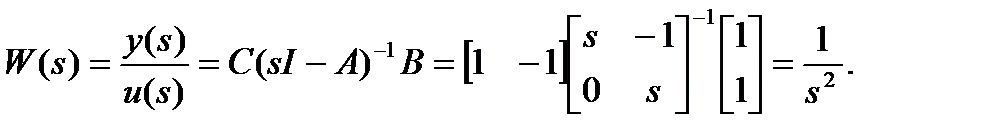
Таким образом, разным представлениям в пространстве состояний соответствует одна и та же ПФ.

Можно показать в общем виде, что преобразования подобия не меняют ПФ объекта.

.

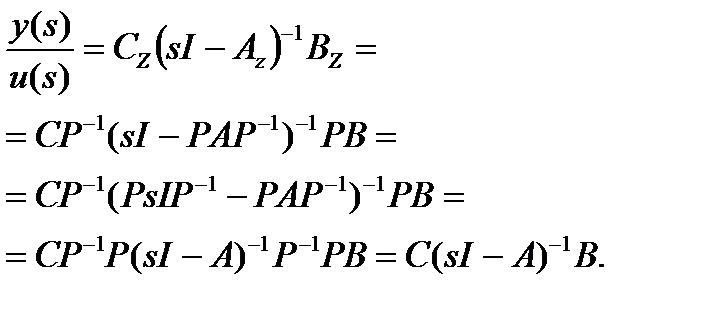Соответственно, можно сделать вывод, что при преобразованиях подобия не меняются и корни характеристического уравнения.

Можно также показать, что преобразования подобия не изменяют такие свойства системы как управляемость и наблюдаемость.

Например, рассмотрим преобразование матрицы управляемости.