Каноническая форма управляемости

Задача выбора переменных состояния в общем случае неоднозначна, однако для скалярных систем существуют стандартные алгоритмы перехода от дифференциального уравнения, описывающего систему, к уравнениям состояния.

Рассмотрим систему с одним входом и одним выходом (рис. 1.7).

W

u(t)

y(t)

Рис. 1.7. Одномерная система

Связь между входом и выходом описывается соотношением

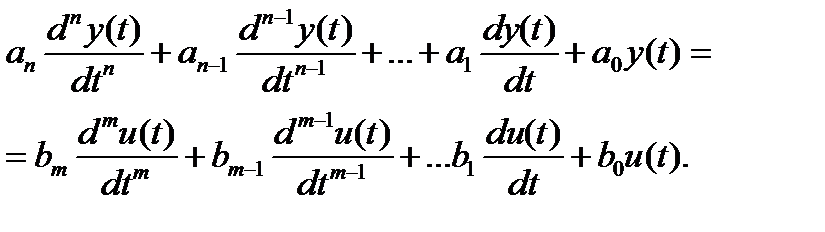
Обозначая через s оператор дифференцирования:

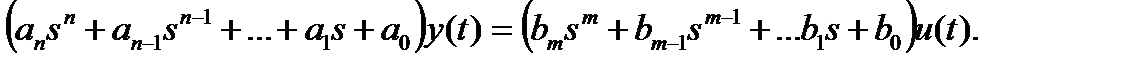
Введем обозначения:

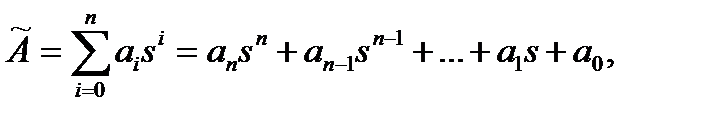
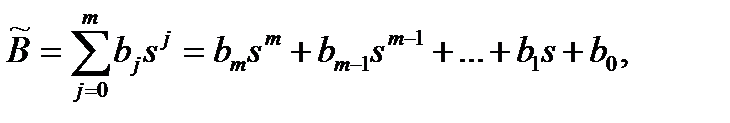
тогда можно записать:

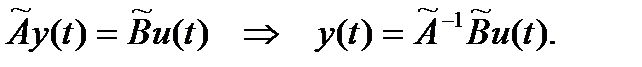
Вводя обозначение:

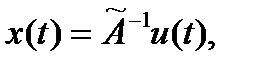
имеем:

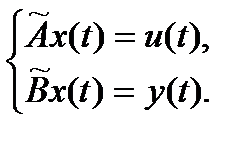
Пусть переменные состояния определяются соотношением:

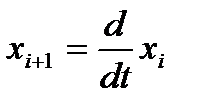
Тогда можно записать:

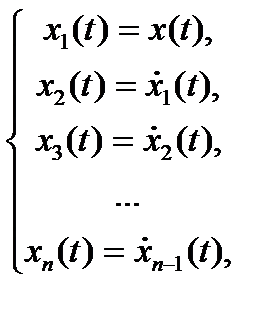
Рассмотрим еще раз уравнение

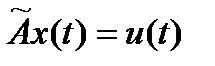
в развернутом виде:

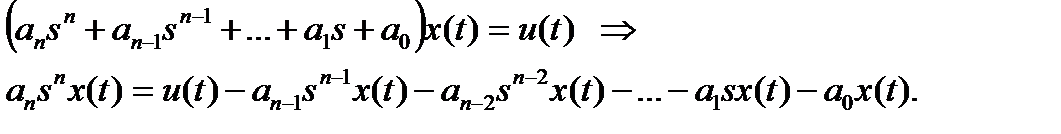
откуда следует

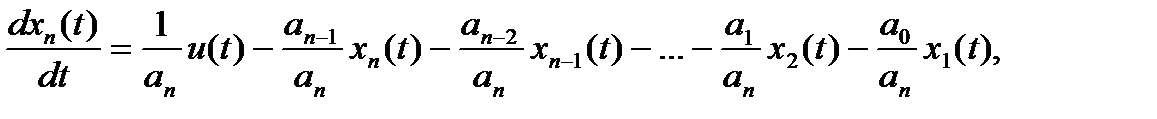
окончательно в матричной форме получается:

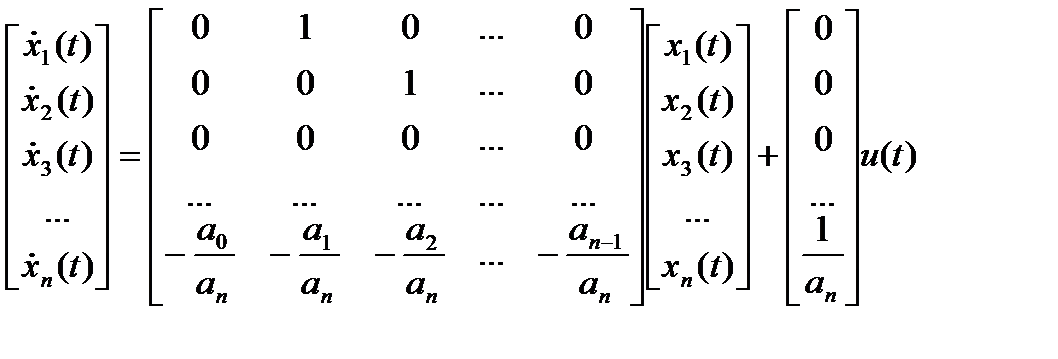
Такое представление уравнений состояния называется канонической формой Фробениуса, или канонической формой управляемости.

Рассмотрим еще раз уравнение

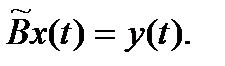
В развернутом виде:

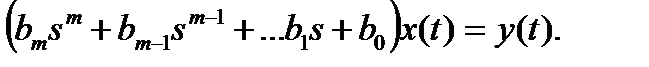
Поскольку m ≤ n (условие физической реализуемости), можно положить m = n при равенстве нулю коэффициентов b_i с индексами i > m.

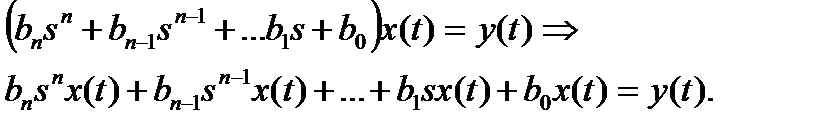
Тогда при использовании введенных переменных состояния следует:

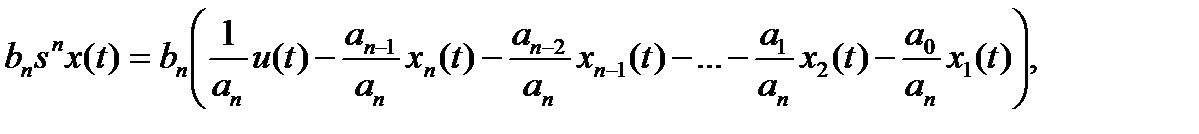
и, окончательно,

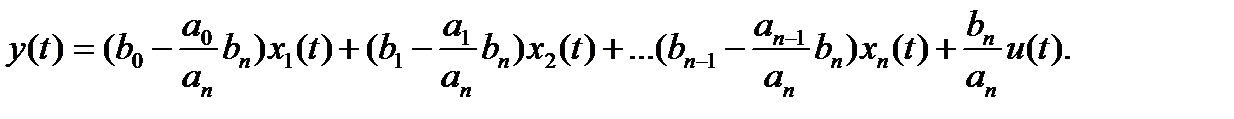
Таким образом, в канонической форме управляемости уравнения состояния имеют вид:

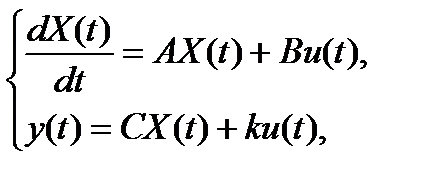
где

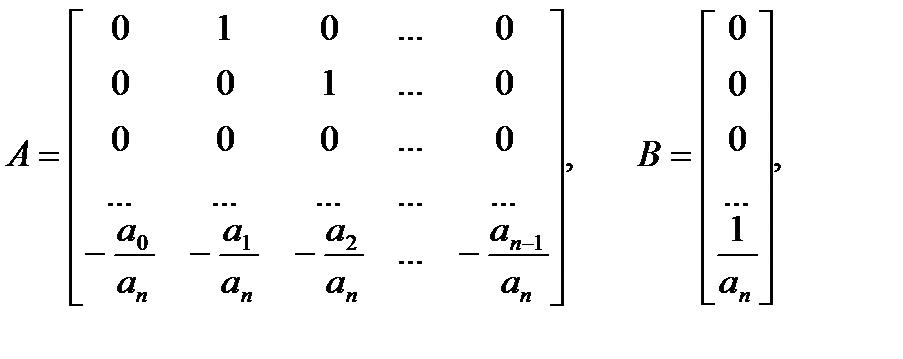
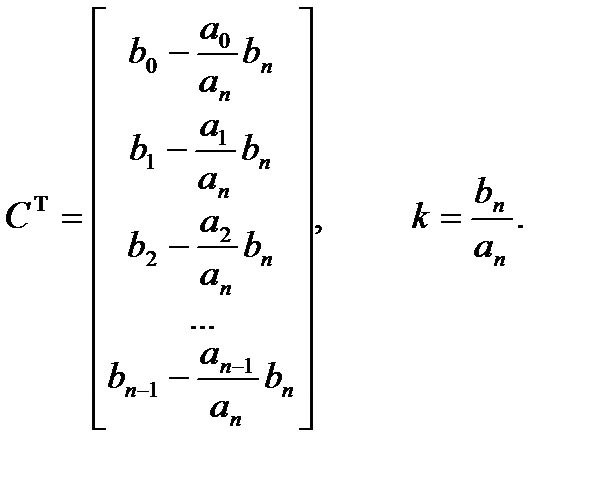
Пример 1.8. Пусть объект управления описывается ПФ:

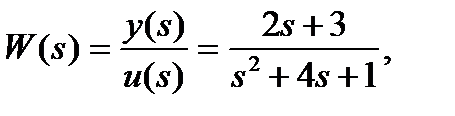
тогда

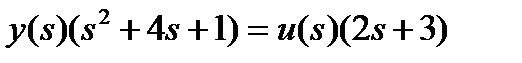
и, очевидно,

b₂=0, b₁=2, b₀=3.

a₂=1, a₁=4, a₀=1.

Уравнения состояния в канонической форме управляемости приобретают вид:

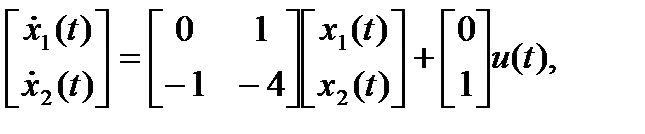
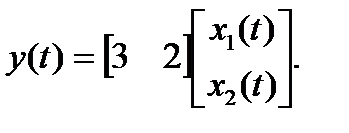
Пример 1.9. Апериодическое звено 1-го порядка:

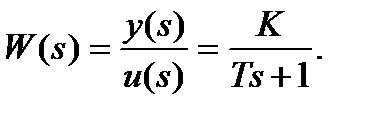
Здесь

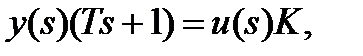
b₀=K, a₁=T, a₀=1.

Получается система уравнений

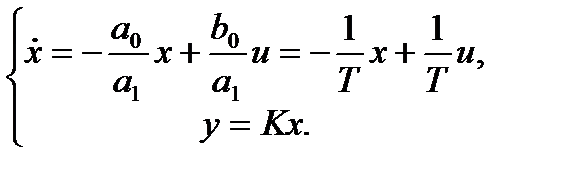
Этой системе соответствует система, приведенная на рис. 1.8.

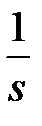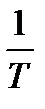u(t)

y(t)

K

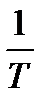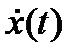x(t)

Рис. 1.8. Апериодическое звено 1-го порядка

Пример 1.10. Запишем уравнения состояния для системы, приведенной на рис. 1.9.

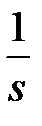u(t)

x2(t)

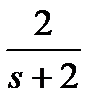x1(t)

Рис. 1.9. Пример динамической системы

Передаточная функция системы:

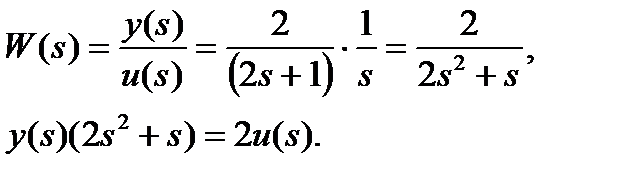
b₀=2, a₂=2, a₁=1, a₀=0.

Уравнения состояния:

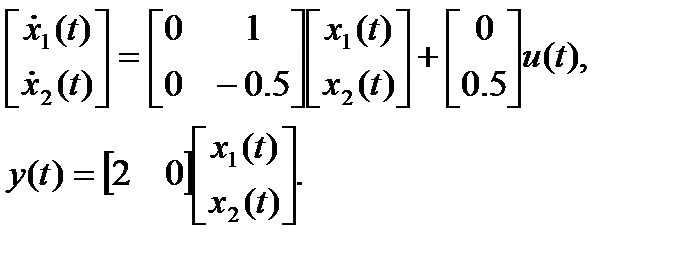
Пример 1.11. Пусть задана передаточная функция

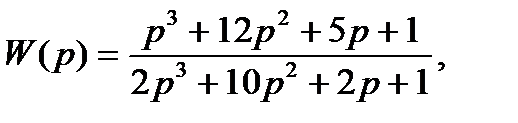
здесь

b₃= 1, b₂= 12, b₁ = 5, b₀=1,

a₃,= 2, a₂,= 10, a₁=2, a₀=1.

Используя каноническую форму управляемости, получаем:

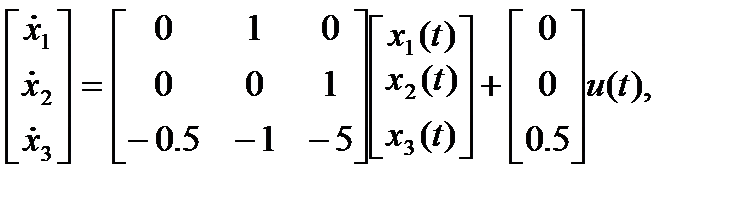
Кроме канонической формы управляемости существует каноническая форма наблюдаемости, в которой наиболее простой вид имеет матрица С.

В канонической форме наблюдаемости уравнения состояния имеют вид:

.

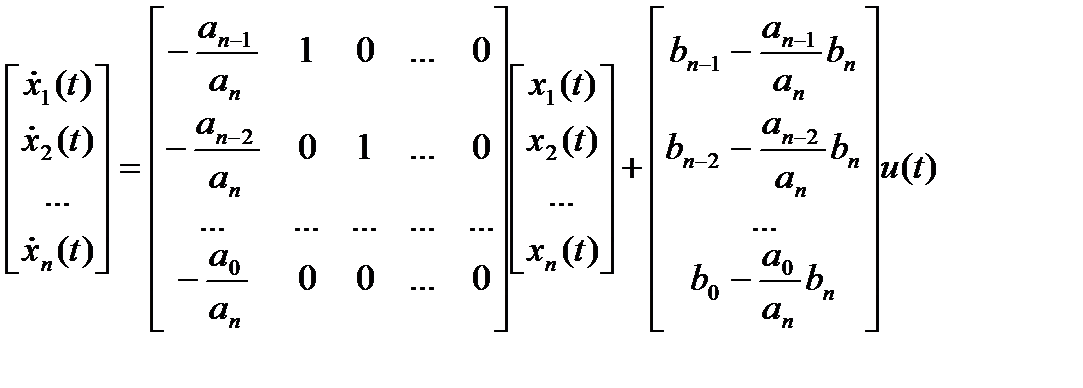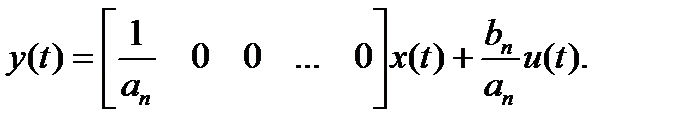
Таким образом, описанный алгоритм получения канонической формы управляемости скалярной системы позволяет легко выполнять переход от описания системы, заданного ПФ, к описанию в пространстве состояний.

Поскольку выбор переменных состояния неоднозначен, одной и той же ПФ могут соответствовать разные модели в пространстве состояний, но при обратном переходе всем этим моделям соответствует одна и та же ПФ.

Иногда ПФ называют внешней моделью системы, а представление в пространстве состояний – внутренней моделью.