КПД передачи винт-гайка. Явление самоторможения.

Передачу винт-гайку приближенно можно представить в виде ползуна двигающегося по наклонной плоскости, которая получается путем развертки средней винтовой резьбы на плоскость.

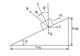р-шаг

z-число заходов

ψ-угол подъема средней винтовой линии

ψ=arctg(zp/πd_ср)

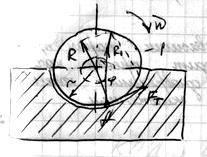
прямой ход (подъем ползуна)

Q-осевая нагр., F-движ., R-полная реакц., φ-угол трения

φ =arctg(f), F+Q+R=0

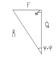Движ. момент: M_д=Fr_ср=Qr_срtg(ψ+ φ)

η=M⁰_д/М_д φ=0 М⁰_д=Qr_срtg ψ η_пр=tg ψ/tg(ψ+ φ) (1)

Обратный ход: Q-движ. сила, F-тормозящая сила

η_обр=tg(ψ-φ)/tg(ψ) (2)

Если ψ<= φ, то η_обр<=0 винтовая пара является самотормозящей.

Динамическое и статическое уравновешивание вращающихся звеньев. Виды неуравновешенности, их оценка и способы устранения. Балансировка.

Уравновешивание масс состоит в устранении переменных реакций на опоры от сил инерции. Для полного устранения этих реакций главный вектор сил инерции и главный момент сил инерции должны быть равны нулю.

При F_и=0 и М_и=0 это динамическое уравновеш.

При F_и=0 а М_и≠0 это статическое уравновешивание

Виды неуравновешенности:

Статическая неуравновешенность: r_s≠0, I_xz=I_yz=0 следовательно F_и≠0, M_и=0

Мерой стат. Неуравновеш. Явл. Дисбаланс: D=mr_s, F_и=Dω²

Моментная неуравновешенность:

r_s=0, I_xz≠0, I_yz≠0 следовательно F_и=0, M_и≠0

Динамическая неуравновешенность:

r_s≠0, , I_xz≠0, I_yz≠0 следовательно F_и≠0, M_и≠0

Балансировка-экспериментальное устранение уравновешенности

Уравновешивание нескольких масс, вращающихся на одном валу

Пример: уравновесить массы 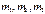, вращающиеся на одном валу.

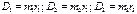
Каждый дисбаланс раскладываем

на 2 параллельных:

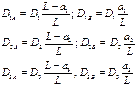
Условие уравновешенности:

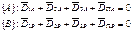
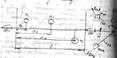
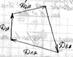
Строим многоугольники дисбалансов: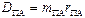

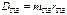
Статическое уравновешивание масс плоских рычажных механизмов

Для механизмов в целом чаще всего ограничиваются статическим уравновешиванием, когда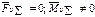

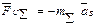
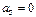, то есть общий центр масс всего механизма должен быть неподвижным.

Рассмотрим задачу статического уравновешивания масс кривошипно – ползунного механизма:

Статическое размещение масс.

Согласно этому методу, твердое

тело

заменяется системой

сосредоточенных

(точечных) масс, которые

обладают той

же массой и тем же расположением

центра масс, что и заменяемое тело.

Из этих уравнений находим:

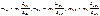
В результате в точке “A” сосредоточена вращающаяся масса: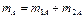

В точке “B” – поступательно движущаяся масса.

На продолжении звена “2” в точке “C” устанавливаем противовес, массу которого 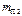находим из условия, что бы центр масс 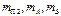, оказался точке “A”.

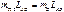
В точке “D” устанавливаем противовес, массу которого находим из условия, что бы центр масс 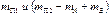оказался в точке “O”.

После установки обоих противовесов общий центр масс общий центр масс механизма окажется в неподвижной точке “O”, где достигается статическое уравновешивание.