Раздел 1. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ, ПРОИЗВОДНАЯ И ЕЕ ПРИЛОЖЕНИЯ

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Государственное образовательное учреждение высшего образования «Тюменский государственный нефтегазовый университет»

Нефтегазовый колледж им. Ю.Г. Эрвье

МАТЕМАТИКА

Программа, методические указания и контрольные задания

для студентов специальности

21.02.01 – Разработка и эксплуатация нефтяных и газовых месторождений

заочного отделения

2 курс, 3-4 семестр

Тюмень, 2016

Рассмотрено: УТВЕРЖДАЮ

на заседании цикловой комиссии Зам. директора по УПР

Протокол № ____ _____________________

от «____» _______2016г

Председатель ЦК: «____»__________2016г.

Соответствует государственным

требованиям к минимуму содержа-

ния и уровню подготовки выпускни-

ков по специальности

Составитель: Калистова А.В.

Часть 1.Введение

В настоящее время математические методы широко используются для разрешения самых разнообразных задач науки, техники. Значение этих методов существенно выросло в связи с массовым применением во всех отраслях народного хозяйства электронно-вычислительной машин (ЭВМ).

Математика является фундаментальной дисциплиной. Цель ее преподавания в среднем учебном заведении предусматривает:

- развить логическое мышление и повысить общий уровень математической культуры;

- познакомить студентов с математическим аппаратом, необходим для изучения общенаучных общеинженерных дисциплин;

- выработать у студентов умение самостоятельно изучать учебную литературу по математике и ее приложениям;

- выработать навыки к математическому исследованною прикладных вопросов и научить переводить инженерную задачу на математический язык, использовать для решения этих задач ЭВМ.

Часть 2. Общие рекомендации

студенту-заочнику по работе над курсом математики

Основной формой обучения студента - заочника является самостоятельная работа над учебным материалом, которая состоит из следующих элементов: изучение материала по учебнику, решение задач, самопроверка, выполнение контрольных работ. Во время сессии студенты слушают лекции, посещают практические занятия, сдают устные зачеты и экзамены. При самостоятельном изучении учебного материала можно использовать следующие рекомендации.

I. Чтение учебника

1. Каждый последующий вопрос должен изучаться только после правильного понимания предыдущего

2. Особое внимание следует обращать на определение основных понятий. Их следует знать четко, а также подробно разбирать примеры, которые поясняют такие определения и уметь строить аналогичные примеры самостоятельно.

3. При изучении материала по учебнику полезно вести конспект, в который рекомендуется выписывать определения формулировки теорем формулы, уравнения и т.д. На полях конспекта следует отмечать вопросы, на которые необходимо получение устной или письменной консультации преподавателя.

4. Выводы, полученные в виде формул, рекомендуется подчеркивать или обводить рамкой, чтобы при перечитывании они выделились и лучше запоминались. Полезно составить лист, содержащий важнейшие и наиболее часто употребляемые формулы курса. Такой лист поможет запомнить эти формулы, а также служит постоянным справочником.

II. Решение задач

1. Чтение учебника должно сопровождаться решением задач, для чего рекомендуется завести специальную тетрадь.

2. Решение задач и примеров следует излагать подробно, обосновывая каждый этап решения теоретическими положениями курса. Чертежи можно выполнять от руки, но аккуратно в соответствии с данными условиями.

3. В промежуточных вычислениях не следует вводить приближенные значения корней, числа π, и т.п. Следует обратить внимание соответствует ли полученный ответ существу данной задачи. Полезно так же решить задачу несколькими способами и сравнит полученные результаты.

III. Самопроверка

1. После изучения определенной темы по учебнику и решения достаточного количества соответствующих задач студенту рекомендуется воспроизвести по памяти определения, выводы, формулировки и доказательства теорем. При недостаточном усвоении надо еще раз внимательно разобраться в материале учебника.

2. Важным критерием усвоения теории является умение решать задачи на пройденный материал. Тем не менее, благополучное решение задач нельзя считать достаточным признаком усвоения теории. Часто правильное решение получается в результате механического применения формул, без понимания существа дела. Если в процессе работы над изучением теоретического материала или при решении задач у студента возникают вопросы, найти ответ на которые самостоятельно не удается, то он может обратиться к преподавателю для получения от него письменной или устной консультации, которые проводятся каждую субботу на кафедре высшей математики.

Часть 3. Правила выполнения и оформления контрольных работ

При выполнении контрольных работ необходимо строго придерживаться указанных ниже правил. Работы, выполненные без соблюдений этих правил, не зачитываются и возвращаются студенту для переработки.

1. Каждая контрольная работа должна быть выполнена в отдельной тетради в клетку чернилами любого цвета, кроме красного. Необходимо оставлять поля шириной 4 – см для замечаний рецензента.

2. В заголовке работы на обложке тетради должны быть ясно написаны фамилия студента, его инициалы, учебный номер (шифр), номер контрольной работы, название дисциплины; здесь же следует указать название учебного заведения, дату отсылки работы в институт и адрес студента. В конце работы следует проставить дату ее выполнения и расписаться.

3. В работу должны быть включены все задачи, указанные в задании строго по положенному варианту. Контрольные работы, содержащие не все задачи задания, а так же задачи не своего варианта, не зачитываются.

4. Решения задач надо располагать в порядке номеров, указанных в заданиях, сохраняя номера задач настоящей методички.

5. Перед решением каждой задачи надо полностью выписать ее условие. В том случае, если несколько задач, из которых студент выбирает задачи своего варианта, имеют общую формулировку, следует, переписывая условие задачи, заменить общие данные конкретными, взятыми из соответствующего номера своего варианта.

6. Решения задач следует излагать подробно и аккуратно, объясняя и мотивируя все действия по ходу решения и делая необходимые чертежи.

7. После получения прорецензированной работы, студент должен исправить все отмеченные рецензентом ошибки и недочеты и выполнить все рекомендация рецензента. При высылаемых исправлениях должна обязательно находится прорецензированная работа. Поэтому рекомендуется при выполнении контрольной работы оставлять в конце тетради несколько чистых листов для всех дополнений и исправлений в соответствии с указаниями рецензента. Вносить исправления в сам текст работы после рецензирования запрещается.

8. правило выбора варианта: по последней цифре зачетной книжки (в случае, если последней цифрой является ноль – выбирается 10 вариант)

Часть 4. Содержание курса

Раздел 1. Введение в математический анализ

Производная и ее приложения

1.Функциональная зависимость

2.Обзор элементарных функций

3. Предел и непрерывность функции

4. Неопределенности

5.Производная. Определения. Свойства и формулы.

6. Дифференциал функции

7.Производная высших порядков

8. Приложения исчисления

Раздел 2. Интегральное исчисление

1. Первообразная. Неопределенный интеграл. Определение первообразной. Неопределенный интеграл. Определение первообразной, неопределенного интеграл, обозначение неопределенного интеграла.

2. Таблица основных интегралов

3. Основные свойства неопределенного интеграла: интеграл орт суммы двух функций, от произведения функции на постоянную, от производной и дифференциала.

4. Основные методы интегрирования: непосредственное интегрирование, замена переменной, интегрирование по частям

5. Задача о вычислении площади криволинейной трапеции.

6. Определенный интеграл. Определение интегральной суммы и определенного интеграла. Геометрический смысл. Формула Ньютона-Лейбница для вычисления определенного интеграла.

7. Основные свойства определенного интеграла.

8. Методы вычисления определенного интеграл: замена переменной, по частям.

9. Вычисление площади определенным интегралом

10. Несобственные интегралы. Интеграл на бесконечном промежутке, его сходимость, расходимость.

Функциональная зависимость

Понятие функции и функциональной зависимости является основополагающим в математике. Это понятие тесно связано с понятием числового множества.

Числовым множеством будем называть всякую совокупность вещественных чисел. Каждое вещественное число изображается точкой числовой оси, поэтому всякому числовому множеству можно сопоставить на оси множество точек.

Отрезком [а, b] называется множество чисел х, для которых а £ х £ b. Длина отрезка [а, b] равна b–а.

Интервалом (а, b) называется множество чисел х, для которых а < x < b.

Интервал называют открытым промежутком, отрезок – замкнутым.

Дадим важное в дальнейшем понятие δ-окрестности (δ – дэльта) точки. Пусть х₀ – некоторое число и δ > 0 (положительное число).

Определение. δ-окрестностью числа х₀ называется множество чисел х, удовлетворяющих неравенству х₀–δ < х < х₀+δ.

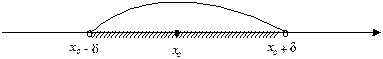Иначе говоря, δ-окрестность точки х₀ – это интервал с центром в точке х₀, длина которого равна 2δ.

Рис. 1.

Используя определение модуля (абсолютной величины) числа, δ-окрестностью числа х₀ можно назвать все те числа х, которые удовлетворяют неравенству |х–х₀|<δ.

Изучая тот или иной процесс, мы сталкиваемся с различными величинами, которые можно разбить на два типа.

Одни величины в данном процессе остаются неизменными. Их называют постояннымивеличинами. Другие в данном процессе изменяются и называются переменными. Например, при движении автомобиля его длина, ширина постоянны, а длина пути, количество бензина в баке являются величинами переменными.

Определение.Множество всех значений переменной величины, которое она принимает в процессе своего изменения, называется множеством ее значений или областью изменения переменной.

Рассматривая некоторый процесс, мы имеем дело со взаимным изменением нескольких величин, когда изменение одной величины влечет изменение другой.

Понятие функциональной зависимости возникло в результате отвлечения от физической сущности взаимно изменяющихся величин и выделения самого факта зависимости.

Определение. Если каждому значению переменной величины х из множества Х ее значений по некоторому правилу сопоставлено определенное значение другой переменной у, то у называется зависимой переменной или функцией от х.

х называется независимой переменной (аргументом); множество Х называется областью определения данной функции. Множество У значений переменной у называется множеством значений функции.

Задать функцию – значит задать и область определения ее и закон соответствия между переменными х и у.

Функция обозначается следующим образом: у=ƒ(x), y=φ(х), у=F(х) и т.п.

Способы задания функции

Аналитический способ задания является одним из самых распространенных и наилучшим образом приспособлен к операциям математического анализа. Функциональная зависимость задается с помощью формулы, аналитического выражения.

Например, 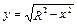. Здесь функция у принимает только неотрицательные значения и определена на множестве, где R²–х² ³ 0, т.е. х²£ R². Если R>0, то –R £ x £ R.

Другой пример: .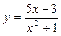

Здесь у – функция, определенная всюду (х – любое число), и принимает любые действительные значения.

Заметим, что к недостаткам аналитического способа следует отнести следующее: не всякую функциональную зависимость можно задать аналитически, найденная формула может быть очень громоздкой и неудобной для исследования, наконец, формула не дает наглядности.

Табличный способ задания знаком из школьного курса (таблицы значений для sinx, cosx, lgx, …). При табличном способе задания выбирается лишь ограниченное число значений аргумента х, и соответствующие им значения функции у заносятся в таблицу.

Недостатком этого способа задания прежде всего является то, что некоторых нужных нам значений функции в таблице может не быть.

Рассмотрим наиболее наглядный способ задания функции.

График и графическое задание функции

В прямоугольной системе координат на плоскости построим множество точек М (х, у), где у=ƒ(х). Полученное множество называется графиком функции ƒ(х). В этом случае уравнение у=ƒ(х) называют уравнением множества точек М.

Как правило, будем рассматривать функции, график которых состоит из одной линии или из совокупности нескольких линий.

График является наглядным и легко обозримым изображением функции и поэтому оказывает большую помощь при изучении ее.

Рассмотрим некоторые общие свойства функций.

Ограниченность функции

Назовем функцию ƒ(х) ограниченной, если для всех х из области ее определения существует такое число D, что |ƒ (х)| < D (D >0).

Например, функции sin x и cos x являются ограниченными.

Монотонные функции

Функция ƒ (х) называется возрастающей в области ее определения Х, если бóльшим значениям аргумента соответствуют и бóльшие значения функции, т. е. для х₁ < х₂ ƒ(х₁) < ƒ(х₂).

Функция ƒ(х) называется убывающей, если для х₁ < х₂ ƒ(х₁) > ƒ (х₂).

Например, функция ƒ(х)=2^х является возрастающей.

Возрастающие и убывающие функции называются монотонными.

Периодические функции

Функция ƒ(х) называется периодической с периодом Т, если равенство

ƒ(х+Т)=ƒ(х)

выполняется для всех х из области определения функции.

Например, sin (х+2π)=sin x, tg (x+π)=tg x. Это значит, что функция sin x – периодическая с периодом 2π, tg х – периодическая с периодом π.

Четные и нечетные функции

Функция ƒ(х) должна быть определена в симметричной относительно начала координат области.

Функция ƒ(х) называется четной, если значение не изменится при замене х на –х, т. е.

ƒ(–х)=ƒ(х).

Если же ƒ(–х)= –ƒ(х), то ƒ(х) – нечетная. Например, х², х⁴, cos x, 1+5·x² – функции четные,

х, х³, sin x, tg x – функции нечетные.

Заметим, что график четной функции симметричен относительно оси ординат Оу, а график нечетной функции симметричен относительно начала координат.

Обзор элементарных функций

Кратко остановимся на основных классах элементарных функций, т. к. все они изучаются в курсе средней школы.

Постоянная функция:

ƒ(х)=с.

График ее – прямая у=с.

Степенная функция:

ƒ(х)=хⁿ,

где n – любое число.

При n четном степенная функция является четной, при n – нечетном – функция нечетная.

Приведем графики функций

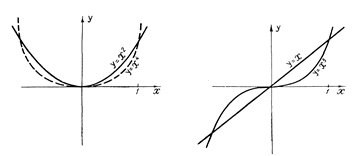ƒ(х)=х, ƒ(х)=х², ƒ(х)=х³, ƒ(х)=х⁴.

Рис. 2. Графики степенных функций

Многочлен (целая рациональная функция):

ƒ(х)=а₀+а₁х+а₂х²+а₃х³+ … +а_nхⁿ.

Частные случаи этой функции – хорошо известные линейная функция ƒ(х)=ах+b (график ее – прямая) и квадратный трехчлен ƒ(х)=ах²+bх+с (график ее – парабола).

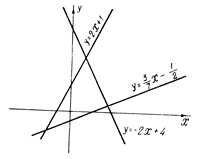Рис. 3. Графики линейных функций

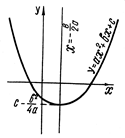Рис. 4. График квадратного трехчлена у=ах²+bх+с, а > 0.

Дробно-линейная функция:

ƒ(х) 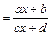.Частным случаем этой функции является обратная пропорциональная зависимость, графиком которой является гипербола .

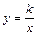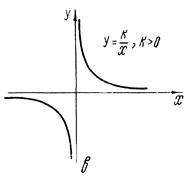
Рис. 5. График дробно-линейной функции.

Показательная функция:

ƒ(х)=а^х, а>0, а¹1.

Эта функция возрастает при а > 1, убывает при 0 < а <1.

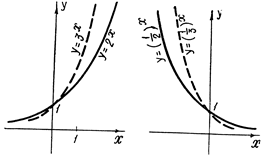
Рис. 6. Графики показательных функций.

Логарифмическая функция:

ƒ(х)=log_ax, a > 0, а¹1

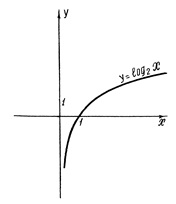
Рис. 7 График логарифмической функции.

Тригонометрические функции

хорошо известны. Приведем их графики

у=sin x, y=cos x, y=tg x, y=ctg x.

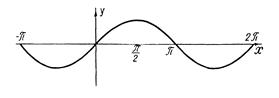
Рис. 8. График y=sin x..

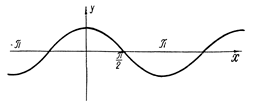
Рис. 9. График у=cos x.

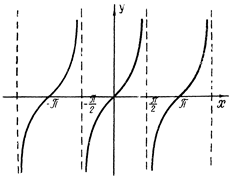
Рис. 10. График у=tg x.

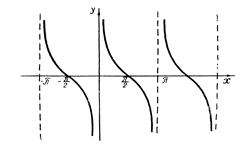
Рис. 11. График у=ctg x.

Односторонние пределы

Пусть дана функция f(x) и точка х₀ внутри области ее определения.

Предел функции f(x) при х, стремящемся к х₀ слева (т.е. при х < х₀), называют левосторонним пределом функции в точке х₀ (или левым пределом) и обозначают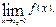

Предел функции f(x) при х, стремящемся к х₀ справа (т.е. при х > х₀), называют правосторонним пределом функции вточке х₀ (или правым пределом) и обозначают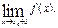

Имеет место следующее утверждение:Если функция /(х) имеет предел А

при 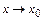, то она имеет в точке х₀ предел слева и предел справа, каждый из которых равен А.

Непрерывность функции

Понятие непрерывности функции интуитивно связано с непрерывностью линии (графика функции). С точки зрения математика это понятие связано с существованием предела функции в точке.

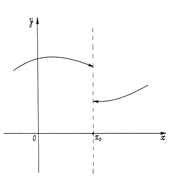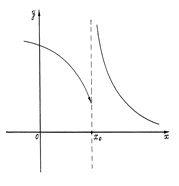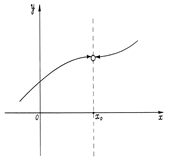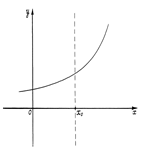Рис. 17. Рис. 18

. Рис. 19. Рис. 20.

На рисунках 17–20 представлены графики различных функций, из которых только одна (рис. 20) является непрерывной в точке х₀. Остальные функции не являются непрерывными в точке по разным причинам. На рис. 17 дан график функции, которая имеет в точке х₀ различные (хотя и конечные) односторонние пределы. На рис. 18 функция в точке х₀ не имеет конечного правого предела. На рис. 19 функция имеет оба равные односторонние пределы, но сама в точке х₀ не определена. Таким образом, для непрерывности функции в точке должны быть устранены все эти особенности.

Определение.Функция ƒ(х) называется непрерывной в точке х₀, если

1) она определена в точке х₀ и в некоторой ее окрестности,

2) существует ,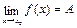

3) предел функции в точке х₀ равен значению функции в

этой точке, т. е.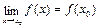

Второе условие определения может быть сформулировано более подробно: существуют и равны оба односторонних предела в точке, т. е.

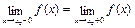
Рассмотрим примеры.

№ 1. .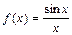

Эта функция не является непрерывной в точке х=0, т. к. в этой точке она не определена.

№ 2. .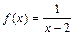

Эта функция не является непрерывной в точке х=2, т. к. в этой точке не существует ее предел: .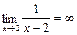

Заметим, что 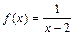в точке х=2 тоже не определена.

№ 3. Зададим функцию с помощью двух аналитических выражений, а именно

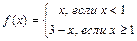
Посмотрим, является ли эта функция непрерывной в точке х=1. Значение функции в этой точке ƒ(1)=3–1=2. Функция определена для всех действительных чисел.

Вычислим односторонние пределы. При х < 1 ƒ(х)=х, поэтому

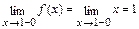
При х > 1 ƒ(х)=3–х, поэтому

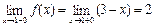
Так как односторонние пределы не равны между собой, то не существует 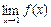и в точке х=1 функция не может быть непрерывной.

Определение. Функция называется непрерывной на отрезке, если она

непрерывна в каждой точке этого отрезка.

Рассматривая простейшие элементарные функции, легко убедится, что каждая из них непрерывна в области своего определения.

Определение.Точка х=х₀ называется точкой разрыва функции, если в

этой точке нарушается хотя бы одно требование

непрерывности.

На рисунках 17–19 приведены примеры точек разрыва.

Точку называют точкой разрыва первого рода, если существуют и конечны оба односторонних предела.

Точку разрыва называют точкой разрыва второго рода, если хотя бы один односторонний предел в этой точке не существует (или бесконечен).

В рассмотренном примере № 3 функция 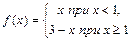имеет в точке х=1 точку разрыва первого рода.

График этой функции состоит из двух полупрямых у=х (для х < 1) и у=3–х (для х ³ 1).

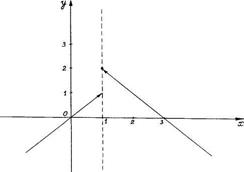
Рис. 21.

При исследовании функции на непрерывность точку разрыва следует искать там, где функция не определена, или в точках, где одно аналитическое выражение функции меняется на другое.

Укажем некоторые свойства непрерывных функций.

1. Если функции ƒ(х) и φ(х) непрерывны в точке х₀, то непрерывны в точке х₀ функции ƒ(х)±φ(х), ƒ(х)·φ(х), .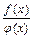

Заметим, что 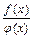непрерывна в точке х₀ только, если φ(х₀)¹0.

2. Каждая элементарная функция непрерывна в своей области определения.

3. Непрерывная на отрезке функция принимает на этом отрезке свое наибольшее и свое наименьшее значения.

4. Если функция ƒ(х) непрерывна на отрезке [а, b] и ƒ(а)=А, ƒ(b)=В, то каково бы ни было число С (А < С < В), найдется точка х=с внутри отрезка [а, b] такая, что

ƒ(с)=С

То есть функция принимает на отрезке все промежуточные значения.

5. Если функция ƒ(х) непрерывна на отрезке [а, b] и принимает на концах его значения разных знаков (ƒ(а)·ƒ(b) < 0), то внутри отрезка найдется точка х=с такая, что ƒ(с)=0. Это свойство позволяет приближенно находить корень уравнения, т. к. если ƒ(с)=0, то с – решение уравнения ƒ(х)=0.

Неопределенности

Теоремы о пределах функций, о бесконечно малых функциях облегчают нахождение пределов. Рассмотрим так называемые неопределенные выражения, когда эти теоремы не применимы. Например, теорема о пределе частного не применима для отношения двух бесконечно малых или двух бесконечно больших функций.

Пусть α(х) и β(х) – бесконечно малые при 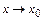; u(x)и v(x) – бесконечно большие при х®х₀. Тогда можно рассматривать пределы при х®х₀ таких, неопределенных для х=х₀, выражений (называемых неопределенностями):

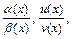α(х)·u(x), u(x)–v(x), которые условно обозначают символами 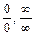, 0·∞, ∞–∞.

Раскрытие неопределенностей (т. е. нахождение пределов неопределенных выражений) происходит с применением некоторых простейших приемов, которые позволят применить теоремы о пределах.

Рассмотрим эти приемы на примерах.

Пример 1.

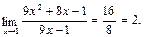
Здесь применима теорема о пределе частного. К этому же выражению при х® 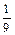теорема о пределе неприменима, т. к. 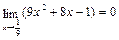и .

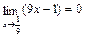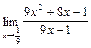представляет собой неопределенность вида .

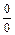Разложим на множители квадратный трехчлен.

9х²+8х–1=9·(х– 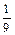)·(х+1).

Для этого достаточно найти корни х₁ и х₂ квадратного трехчлена

ах²+bх+с=а(х–х₁)·(х–х₂).

Под знаком предела сократим одинаковые множители и перейдем к пределу:

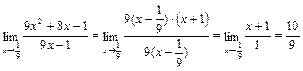
Пример 2.

.

Обнаружив неопределенность 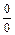(так это в примере и записывают), раскладываем многочлены в числителе и в знаменателе на множители.

Сократив на х–1, получили дробь 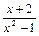, числитель которой стремится к конечному пределу, отличному от нуля ( 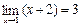), а знаменатель при х®1 является бесконечно малой, тогда дробь при х®1 является бесконечно большой.

Пример 3.

.

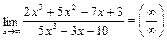Здесь числитель и знаменатель не имеют конечных пределов, имеем неопределенность 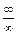. Поделив одновременно числитель и знаменатель на х³, получим

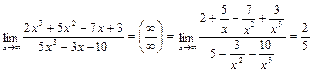, т. к. каждая из дробей 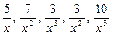является бесконечно малой и стремится к нулю.

Пример 4.

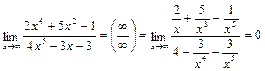, так как

.

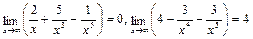Для раскрытия неопределенности 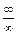следует числитель и знаменатель разделить на одну и ту же старшую степень переменной.

Неопределенности вида 0·∞ и ∞–∞ приводятся к неопределенностям 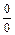или .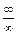

Пример 5.

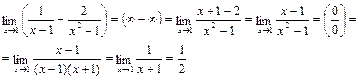
После приведения данных дробей к общему знаменателю была получена дробь, представляющая собой неопределенность .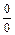

Пример 6.

.

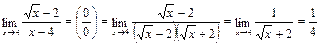Здесь удалось избавиться от разности ( 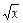–2), стремящейся к нулю при х®4, разложив х–4 на множители по формуле разности квадратов.

Пример 7.

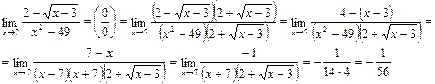
В этом примере нужно было избавиться от радикалов, для чего умножили и числитель и знаменатель на сумму – сопряженное числителю выражение. Применив формулу разности квадратов в числителе, мы избавились от радикалов:

.

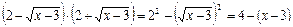Пример 8.

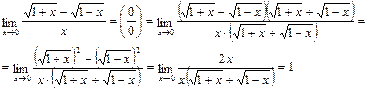
При вычислении пределов выражений, содержащих тригонометрические функции, используется первый замечательный предел: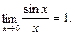

Чтобы подчеркнуть, что первый замечательный предел представляет собой неопределенность 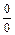, т. е. отношение двух бесконечно малых, записывают его формулу в виде:

,

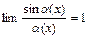если α(х) – бесконечно малая функция. Заметим, что, например, 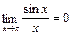не является замечательным пределом.

Пример 9.

.

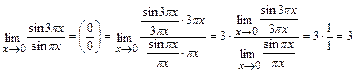При вычислении этого предела прежде всего обнаружили неопределенность 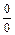. Чтобы использовать первый замечательный предел, разделим sin3πх (и умножим) на 3πх, затем и знаменатель sin πх разделим (и умножим) на πх. Сократив общие множители вынесем множитель 3 и, перейдя к пределу в числителе ( 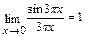) и в знаменателе ( 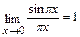), получим искомый предел.

Пример 10.

.

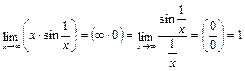Принимая 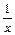=α(х) (бесконечно малая при х®∞), используем

.

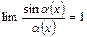Пример 1.

у=(3–2 sin5x)⁴ |Применяем формулы производных для и^α, sin u|

y¢=4·(3–2·sin5x)³·(3–2sin5x)¢=4·(3–2·sin5x)³·(0–2·cos5x·5) = –40·(3–2·sin5x)³.

Пример 2.

.

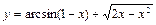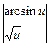
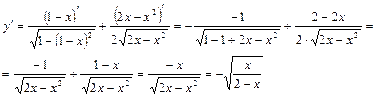
Пример 3.

.

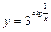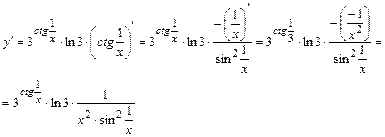
Пример 4.

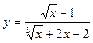
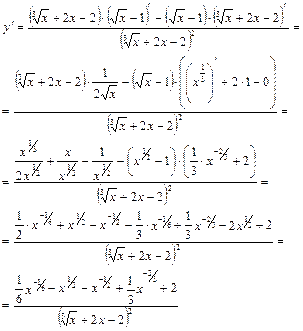
Пример 5.

.

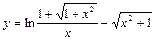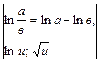
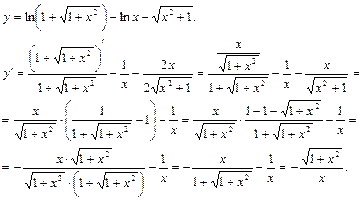
Пример 6.

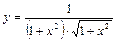Запишем функцию так, чтобы упростить процесс дифференцирования

.

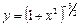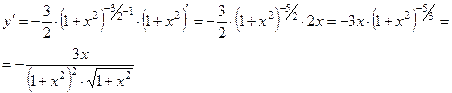
Пример 7.

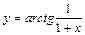
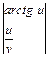
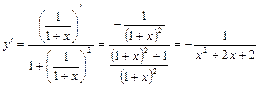
Пример 8.

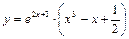
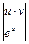
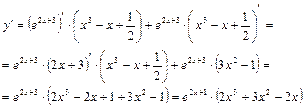
Пример 9.

.

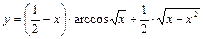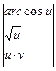
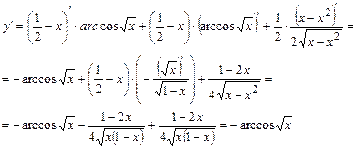
Пример 10.

Составить уравнение касательной к параболе у=х²–4х в точке, где х=1.

Уравнение касательной у-у₀=ƒ¢(х₀)·(х–х₀), где х₀, у₀ – координаты точки касания.

Дано, что х₀=1. Из уравнения параболы найдем у₀=у(х₀)=у(1)=1²–4·1= –3.

Уравнение параболы у=х²–4х, т. е. ƒ(х)=х²–4х. Найдем ƒ¢(х₀).

ƒ¢(х)=2х–4. ƒ¢(х₀)=ƒ¢(1)=2·1–4= –2.

Уравнение касательной:

у+3= –2·(х–1) или 2х+у+1=0

Пример 11.

Дана кривая 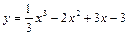. Составить уравнения касательных к этой кривой, параллельных

а) оси Ох, б) прямой3х–у–5=0.

Найдем производную от у:

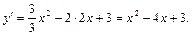
а) Если касательная параллельна оси Ох, то угловой коэффициент ее равен нулю, т. е. производная в точке х₀ должна быть равна нулю: х²–4х+3=0. Решая это уравнение, находим х₁=3 и х₂=1. Найдем соответствующие им значения функции:

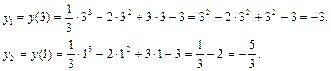
Получены две точки на данной кривой: М₁(3, –3) и М₂(1, ).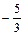

Касательные – прямые, проходящие параллельно оси Ох, имеют уравнения: у= –3 и у= .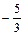

б) Если касательная параллельна прямой 3х-у-5=0, то ее угловой коэффициент равен угловому коэффициенту данной прямой:

3х–у–5=0 или у=3х–5.

k=3.

Производная у¢ в точке х₀ должна быть равна 3.

х²–4х+3=3. Решая это уравнение х²–4х=0, находим х₁=0 и х₂=4.

Найдем соответствующие им значения функции:

у₁=у(0)= –3. у₂=у(4)= 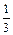·4³–2·4²+3·4–3= – .

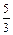Уравнение касательной в точке М₁(0,–3):

у+3=3·(х–0) или 3х–у–3=0.

Уравнение касательной в точке М₂(4, – ):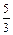

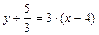или 9х–3у–41=0.

Дифференциал функции

Пусть функция у=ƒ(х) определена на множества Х и дифференцируема в каждой его точке.

Определение. Дифференциалом функ