Реализация типовых задач на компьютере

Excel позволяет при построении уравнения линейной регрессии большую часть работы сделать очень быстро. Для этого необходимо воспользоваться надстройкой Пакета анализа. В меню Сервиз → Анализ данных → Регрессия появляется диалоговое окно, которое нужно заполнить:

Входной интервал У - указывается ссылка на ячейки, содержащие значение результативного признака у.

Входной интервал Х - указывается ссылка на ячейки, содержащие значения факторов х₁,…,х_р (р ≤ 16).

Уровень надежности (доверительная вероятность) - по умолчанию предполагается равным 95%. Если исследователя это значение не устраивает, то рядом выставляют флажок и указывают требуемое значение.

Константа ноль - уравнение со свободным членом равным нулем b₀ = 0.

Метки - если во входные интервалы введены заглавия результативного признака и независимых факторов, то необходимо выставить флажок.

Выходной интервал - достаточно указать левую верхнюю ячейку будущего диапазона.

Новый рабочий лист - можно задать произвольное имя нового листа.

Если необходимо получить дополнительную информацию Остатки и График остатков, то нужно выставить рядом флажок. Для получения результата ― ОК.

ВЫВОД ИТОГОВ
Регрессионная статистика
Множественный R	R
R-квадрат	R2
Нормированный R-квадрат	R2скор
Стандартная ошибка	S
Наблюдения	n

Дисперсионный анализ

df

SS

MS

F

Значимость F

Регрессия

m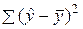

SS/df

F=MSрег/MSост

Р(Fнаб)

Остаток

n-m-1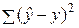

SS/df

Итого

n-1

Сумма

Коэффициенты

Стандартная ошибка

t-статистика

P-значение

Нижние 95%

Верхние 95%

у-пересечение

b0

Sb0

tb0

x1

b1

Sb1

tb1

x2

b2

Sb2

tb2

ВЫВОД ОСТАТКА

Наблюдение

Предсказанный уi

Остатки ei

Если число в графе Значимость F превышает 1 – γ, то принимается гипотеза R² = 0. Иначе принимается гипотеза R² ≠ 0.
Р-значение - это значение уровней значимости, соответствующие вычисленным t-статистикам. Если число в графе Р-значение превышает 1 - γ, то соответствующая переменная статистически незначима и ее можно исключить из модели. Нижние 95% и Верхние 95% - это нижние и верхние границы 95-процентных доверительных интервалов для коэффициентов теоретического уравнения линейной регрессии. Если исследователь согласился с принятым по умолчанию значением доверительной вероятности, то последние два столбца будут дублировать два предыдущих.

Для нахождения статистических характеристик исходных данных также можно воспользоваться Пакетом анализа. Для этого выполняются следующие шаги: Сервиз → Анализ данных → Описательная статистика → ОК. Заполняем диалоговое окно:

Входной интервал - диапазон, содержащий анализируемые данные, это может быть одна или несколько строк (столбцов).

Группирование - выставить флажок по столбцам или строкам.

Метки - флажок, который указывает, содержит ли первая строка названия столбцов или нет.

Выходной интервал - достаточно указать левую верхнюю ячейку будущего диапазона.

Новый рабочий лист - можно задать произвольное имя нового листа.

Если необходимо получить дополнительную информацию Итоговая статистика и k-го наибольшего и k-го наименьшего, то нужно выставить рядом флажок, для получения результата - ОК. Получим таблицу:

уi

Среднее

Стандартная ошибка

Медиана

Мода

Стандартное отклонение

Дисперсия выборки

Эксцесс

Асимметричность

Интервал

Минимум

Максимум

Сумма

Счет

Excel позволяет определить матрицу парных коэффициентов корреляции: Сервиз → Анализ данных → Корреляция → ОК.

Построение графиков осуществляется с помощью Мастера диаграмм:

1) в окне тип выбрать Точечная; вид графика выбрать в поле рядом со списком типов. Щелкнуть Далее;

2) вкладка Ряд -добавить, ввести входные данные для х и у → Далее;

3)заполнить параметры на разных закладках: название диаграммы и осей, параметры легенды и т.д. → Далее;

4) указать место размещения диаграммы на отдельном или имеющемся листе → Готово.

Параметры диаграммы можно менять, используя меню Диаграмм или контекстное меню, вызываемое щелчком правой кнопки мыши. В частности, целесообразно задавать новые значения шкалы осей, чтобы расположить графики наилучшим образом.

С помощью Мастера функций можно получить различные вспомогательные вычисления.

Так, для нахождения транспонированной матрицы Х^Т воспользуемся категорией Ссылки и массивы. Выберем команду ТРАНСП и введем в массив матрицу Х → ОК. Выделим все ячейки, где будет содержаться транспонированная матрица, и для получения массива нажимаем комбинацию клавиш CTRL+SHIFT+

+ENTER.

Для нахождения математических операций пользуемся категорией Математические:

- Х^Т·Х - МУМНОЖ → в первый массив введем матрицу Х^Т, во второй массив - Х → ОК. Выделяем все ячейки, где будет содержаться итоговый результат, и для получения массива нажимаем комбинацию клавиш CTRL+SHIFT+ENTER. Аналогично определяется умножение матрицы на вектор или произведение векторов;

- обратная матрица Х^-1 → МУМНОЖ → в массив введем матрицу Х → ОК. Выделим все ячейки, где будет содержаться обратная матрица, → CTRL+SHIFT+ENTER;

- определитель матрицы Х → МОПР → массив матрицы Х → ОК;

- абсолютное значение х - ABS → коэффициент х → ОК;

- логарифмированное значение х - LN→ коэффициент х → ОК.

Для вычисления различных статистических характеристик используется категория Статистические:

- F_кр - FРАСПРОБР → вероятность α; степени свободы - р; степени свободы - n - p - 1 → OK;

- t_кр ― СТЬЮДРАСПРОБР → вероятность α; степени свободы ― n – p - 1 → OK;

- u_кр - НОРМСТОБР → вероятность 1 - α/2→ OK;

- χ²_кр - ХИ2РАСПРОБР → вероятность α; степени свободы - 0,5(n² - n) → OK;

- среднее значение 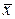- СРЕДЗНАЧ → столбец значений Х → OK;

- среднее квадратичное отклонение σ_х - СТАНДОКЛОН → столбец значений Х → OK;

- РАНГ → число - значение переменной, для которой определяется ранг в наборе данных; ссылка - массив, где содержится ячейка; порядок - 0, если ранг определяется по убыванию, и 1, если по возрастанию.

2. Индивидуальные задания
к контрольной работе

Задание 1.По территориям некоторых регионов известны данные за год по среднедневной заработной плате у (р.) и среднедушевому прожиточному минимуму в день одного трудоспособного х (р.). Требуется:

1. Построить выборочное уравнение парной линейной регрессии. Найти коэффициент эластичности.

2. На уровне значимости α = 0,05 оценить значимость уравнения и коэффициентов регрессии. Для значимых коэффициентов регрессии построить доверительные интервалы.

3. Оценить качество уравнения с помощью средней ошибки аппроксимации.

4. Оценить тесноту связи между переменными с помощью выборочного коэффициента корреляции, построить доверительный интервал.

5. Построить графики зависимостей у_i и 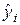от х, а также доверительный интервал для значений у_i.

6. Определить прогнозное значение результативного признака, если возможное значение факторного признака составит 1,9 от его среднего уровня по совокупности. Найти доверительные интервалы для прогнозного значения.

7. Построить уравнения регресси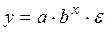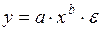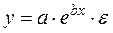й: , , и 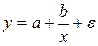, сделать вывод по наилучшей модели

Вариант 1

n
y
x

Вариант 2

n
y
x

Вариант 3

n
y
x

Вариант 4

n
y
x

Вариант 5

n
y
x

Вариант 6

n
y
x

Вариант 7

n
y
x

Вариант 8

n
y
x

Вариант 9

n
y
x

Вариант 10

n
y
x

Задание 2.По 20 предприятиям региона изучается зависимость выработки продукции на одного работника у (тыс. р.) от ввода в действие новых основных фондов х₁ (% от стоимости фондов на конец года) и от удельного веса рабочих высокой квалификации в общей численности рабочих х₂ (%):

1. Построить выборочное уравнение линейной множественной регрессии. Привести полученное уравнение к стандартизированному виду, сделать выводы о влиянии факторов на результирующий фактор. Определить коэффициенты эластичности.

2. Проверить статистическую значимость уравнения регрессии с помощью дисперсионного анализа и через коэффициент детерминации.

3. Проверить статистическую значимость параметров уравнения регрессии и для значимых коэффициентов построить доверительные интервалы.

4. Найти среднюю ошибку аппроксимации.

5. Определить парные и частные коэффициенты корреляции, проверить их на значимость. Для значимых коэффициентов построить доверительные интервалы.

6. Рассчитать частные F-критерии Фишера и оценить целесообразность включения в уравнение одного из факторов после другого.

7. Найти прогнозное значение у_i, если х₁ составляет 0,9 от своего среднего значения, х₂ - 1,4 от своегомаксимальное значения, и доверительные интервалы для среднего и индивидуального значения у_0.

Вариант 1

№	y		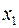	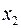№	y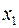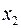
		3,6				6,3
		3,6				6,4
		3,9
		4,1				7,5
		3,9				7,9
		4,5				8,2
		5,3
		5,3				8,6
		5,6				9,5
		6,8

Вариант 2

№	y		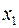	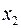№	y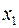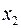
		3,5				6,3
		3,6				6,4
		3,9
		4,1				7,5
		4,2				7,9
		4,5				8,2
		5,3				8,4
		5,3				8,6
		5,6				9,5

Вариант 3

№				№
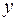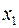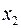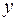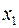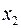		3,7				6,3
		3,7				6,4
		3,9				7,2
		4,1				7,5
		4,2				7,9
		4,9				8,1
		5,3				8,4
		5,1				8,6
		5,6				9,5
		6,1				9,5

Вариант 4

№				№
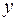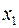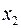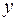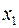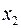		3,5				6,3
		3,6				6,5
		3,9				7,2
		4,1				7,5
		4,2				7,9
		4,5				8,2
		5,3				8,4
		5,5				8,6
		5,6				9,5
		6,1				9,6

Вариант 5

№				№
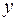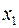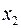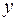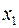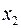		3,6				6,3
		3,6				6,9
		3,7				7,2
		4,1				7,8
		4,3				8,1
		4,5				8,2
		5,4				8,4
		5,5				8,8
		5,8				9,5
		6,1				9,7

Вариант 6

№				№
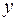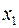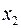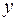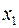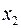		3,5				6,3
		3,6				6,8
		3,8				7,2
		4,2				7,9
		4,3				8,1
		4,7				8,3
		5,4				8,4
		5,6				8,8
		5,9				9,6
		6,1				9,7

Вариант 7

№				№
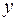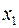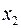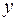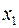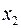		3,8				6,8
		3,8				7,4
		3,9				7,8
		4,1				7,5
		4,6				7,9
		4,5				8,1
		5,3				8,4
		5,5				8,7
		6,1				9,5
		6,8				9,7

Вариант 8

№				№
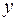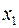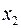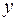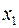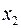		3,8				7,1
		4,1				7,5
		4,3				7,8
		4,1				7,6
		4,6				7,9
		4,7				8,1
		5,3				8,5
		5,5				8,7
		6,9				9,6
		6,8				9,8

Вариант 9

№				№
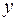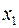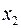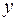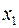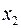		3,9				7,1
		4,2				7,5
		4,3				7,8
		4,4				7,9
		4,6				8,1
		4,8				8,4
		5,3				8,6
		5,7				8,8
		6,9				9,6
		6,8				9,9

Вариант 10

№				№
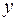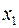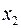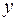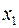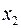		3,6				7,2
		4,1				7,6
		4,3				7,8
		4,4				7,9
		4,5				8,2
		4,8				8,4
		5,3				8,6
		5,6				8,8
		6,7				9,2
		6,9				9,6

Задание 3.Имеются данные об объемах потребления электроэнергии ( 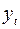) жителями региона за 16 кварталов. Требуется:

1. Построить график временного ряда и определить автокорреляционную функцию. Определить составляющие временного ряда.

2. Если ряд содержит сезонную компоненту, то выявить и устранить ее с помощью статистических методов, построив аддитивную модель (для нечетных вариантов) или мультипликативную модель временного ряда (для четных вариантов). Построить модель с помощью фиктивных переменных.

3. Если ряд содержит тенденцию, то построить уравнении тренда. Сделать прогноз на 2 квартала вперед.

Варианты 1, 2

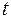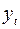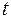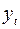	5,8		7,9
	4,5		5,5
	5,1		6,3
	9,1		10,8
	7,0		9,0
	5,0		6,5
	6,0		7,0
	10,1		11,1

Варианты 3, 4

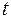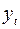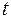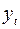	5,5		8,0
	4,6		5,6
	5,0		6,4
	9,2		10,9
	7,1		9,1
	5,1		6,4
	5,9		7,2
	10,0		11,0

Варианты 5, 6

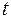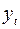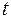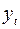	5,3		8,2
	4,7		5,5
	5,2		6,5
	9,1		11,0
	7,0		8,9
	5,0		6,5
	6,0		7,3
	10,1		11,2

Варианты 7, 8

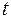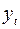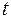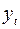	5,5		8,3
	4,8		5,4
	5,1		6,4
	9,0		10,9
	7,1		9,0
	4,9		6,6
	6,1		7,5
	10,0		11,2

Варианты 9, 10

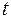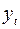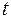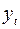	5,6		8,2
	4,7		5,6
	5,2		6,4
	9,1		10,8
	7,0		9,1
	5,1		6,7
	6,0		7,5
	10,2		11,3

Задача 4. По данным приложения провести компонентный анализ (варианты приведены в табл. 20). На основании матрицы собственных значений определить вклад компонент в суммарную дисперсию. Отобрать и указать вклад (m < k) первых главных компонент. Используя матрицу факторных нагрузок А, дать экономическую интерпретацию полученным главным компонентам. Используя вектор значений результативного признака у и матрицу F, построить уравнение регрессии на главные компоненты с максимальным числом значимых коэффициентов регрессии.

Таблица 20

№ варианта	Номера факторных признаков, X	№ варианта	Номера факторных признаков, X
	2, 4, 7, 8, 10		2, 4, 8, 9, 11
	2, 4, 7, 9, 11		3, 7, 8, 9, 10
	4, 7, 8, 9, 11		3, 5, 8, 9, 11
	2, 4, 9, 10, 11		4, 7, 8, 9, 11
	4, 7, 9, 10, 11		4, 5, 9, 10, 11

Задание 5.Предприятия характеризуются следующими экономическими показателями: у, х₁, х₃, х₅, х₆ (данные находятся в приложении). Значения этих показателей представлены в табл. 21. В каждом варианте даны две обучающие выборки.Требуется вычислить оценки значений дискриминантной функции для оставшихся предприятий и провести их классификацию. Дать экономическую интерпретацию результатов дискриминации.

Таблица 21

№ варианта	Группа А	Группа Б
	1,2,4,5,6,8,24,29,30	12,14,15,16,21,23,27,28
	1,2,3,4,5,6,8,24,25	12,14,16,21,23,26,27,30
	1,2,3,5,6,8,11,22,29	12,14,15,16,21,23,28,30
	1,2,3,4,5,6,24,26,29	12,14,15,16,21,27,28,30
	1,2,3,4,5,8,11,24,29	12,14,15,16,23,27,28,29
	1,2,3,4,6,8,10,24,29	12,14,15,21,23,26,27,28
	1,2,3,5,6,8,18,24,29	12,14,16,21,23,27,28,30
	1,2,4,5,6,8,18,24,29	12,15,16,21,23,27,28,30
	1,3,4,5,6,8,18,24,26	14,15,16,21,23,27,28,29
	2,3,4,5,6,8,18,24,29	12,14,15,16,21,23,27,28

Рекомендуемая литература

1. Калайдин Е.Н., Фощан Г.И. Эконометрика: парная регрессия. Краснодар: КубГУ, 2006.

2. Калайдин Е.Н., Фощан Г.И. Эконометрика: множественная регрессия. Краснодар: КубГУ, 2007.

3. Калайдин Е.Н., Подгорнов В.В., Фощан Г.И. Методы прикладной статистики в задачах моделирования социально-экономических систем. Краснодар: КубГУ, 2002.

4. Бородич С.А. Эконометрика: Учеб. пособие. Минск: Новое знание, 2004.

5. Эконометрика: Учебник /Под ред. И.И. Елисеевой. М.: Финансы и статистика, 2001.

6. Эконометрика: Учебник для вузов /Под ред. Н.Ш. Кремера. М.: ЮНИТИ-ДАНА, 2003.

Приложение

№	Y	X1	X2	X3	X4	X5	X6	Х7	Х8
	9,26	0,78	0,40	1,37	1,23	0,23	1,45		167,69
	9,38	0,75	0,26	1,49	1,04	0,39	1,30		186,10
	12,11	0,68	0,40	1,44	1,80	0,43	1,37		220,45
	10,81	0,70	0,50	1,42	0,43	0,18	1,65		169,30
	9,35	0,62	0,40	1,35	0,88	0,15	1,91		39,53
	9,87	0,76	0,19	1,39	0,57	0,34	1,68		40,41
	8,17	0,73	0,25	1,16	1,72	0,38	1,94		102,96
	9,12	0,71	0,44	1,27	1,70	0,09	1,89		37,02
	5,88	0,69	0,17	1,16	0,84	0,14	1,94		45,74
	6,30	0,73	0,39	1,25	0,60	0,21	2,06		40,07
	6,22	0,68	0,33	1,13	0,82	0,42	1,96		45,44
	5,49	0,74	0,25	1,10	0,84	0,05	1,02		41,08
	6,50	0,66	0,32	1,15	0,67	0,29	1,85		136,14
	6,61	0,72	0,02	1,23	1,04	0,48	0,88		42,39
	4,32	0,68	0,06	1,39	0,66	0,41	0,62		37,39
	7,37	0,77	0,15	1,38	0,86	0,62	1,09		101,78
	7,02	0,78	0,08	1,35	0,79	0,56	1,60		47,55
	8,25