Предел. непрерывность. дифференцируемость

ПРЕДЕЛ ФУНКЦИИ В ТОЧКЕ

О п р е д е л е н и е 1.Число называется пределом функции , где , в точке (или при стремлении точки к точке ), если для любого сколь угодно малого найдется такое число что для всех точек из 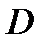, удовлетворяющих условию , справедливо неравенство:

Используется одно из обозначений:

или при

З а м е ч а н и е 1.В приведенном выше определении каким угодно способом, то есть по любой кривой, лежащей в и соединяющей точки и

С в о й с т в а п р е д е л а

С в о й с т в о 1. Если функция имеет предел в точке то этот предел единственный.

С в о й с т в о 2. Пусть функции и определены в некоторой окрестности точки и имеют конечные пределы в этой точке. Тогда в точке существуют пределы функций где в При этом имеют место равенства:

(1)

О п р е д е л е н и е 2.Число называется пределом функции , где , при , если для любого сколь угодно малого найдется такое число что при всех удовлетворяющих условию справедливо неравенство:

При этом используют одно из обозначений:

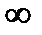О п р е д е л е н и е 3.Говорят, что функция , где , имеет вточке предел, равный , если для любого сколь угодно большого найдется такое число что при всех удовлетворяющих условию справедливо неравенство:

При этом используют одно из обозначений:

П р и м е р 1. Вычислить предел:

Р е ш е н и е. Так как в данном примере

то по формуле (1) находим:

О т в е т:

П р и м е р 2. Вычислить предел:

Р е ш е н и е.

О т в е т:

П р и м е р 3. Вычислить предел:

Р е ш е н и е. а) Пусть по оси Тогда

и

б) Пусть по оси Тогда

и

Следовательно, при функция предела не имеет.

О т в е т: предел не существует.

НЕПРЕРЫВНОСТЬ ФУНКЦИИ

О п р е д е л е н и е 4.Функция , где , называется непрерывной в точке если в этой точке существует предел функции и он равен числу то есть выполняется равенство:

или

Часто используют другое определение, эквивалентное предыдущему.

О п р е д е л е н и е 5. Функция , где , называется непрерывной в точке если бесконечно малым приращениям аргументов соответствует бесконечно малое приращение функции то есть выполняется равенство:

где полное приращение функции в точке

О п р е д е л е н и е 6.Функция , где , называется непрерывной на множестве если она непрерывна в каждой точке

О п р е д е л е н и е 7.Если функция , где , не является непрерывной в точке то точка называется точкой разрыва функции

З а м е ч а н и е 1. Для функции нескольких переменных сохраняют силу теоремы о непрерывности элементарных функций, арифметических действиях над непрерывными функциями, теорема о непрерывности сложной функции, которые изучались ранее в теории функции одной переменной.

П р и м е р 4. Найти точки непрерывности и разрыва функции .

Р е ш е н и е. Функция определена во всех точках плоскости , кроме начала координат. Очевидно, если то справедливо равенство: Следовательно, функция непрерывна в любой точке области определения. Точка – точкой разрыва, т.к.

О т в е т: непрерывна в области ; точка разрыва.

П р и м е р 5. Найти точки разрыва функции .

Р е ш е н и е. Эта функция определена во всех точках плоскости 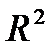за исключением точек единичной окружности с центром в начале координат. Любая точка области определения - точка непрерывности функции. Любая точка единичной окружности является точкой разрыва исходной функции. Действительно, если лежит на окружности , то есть , то справедливо равенство:

Поэтому окружность - линия разрыва функции.

О т в е т: все точки единичной окружности .